Stokes I Simultaneous Image and Instrument Modeling

In this tutorial, we will create a preliminary reconstruction of the 2017 M87 data on April 6 by simultaneously creating an image and model for the instrument. By instrument model, we mean something akin to self-calibration in traditional VLBI imaging terminology. However, unlike traditional self-cal, we will solve for the gains each time we update the image self-consistently. This allows us to model the correlations between gains and the image.

To get started we load Comrade.

julia

using Comrade



using Pyehtim
using LinearAlgebra

For reproducibility we use a stable random number genreator

julia

using StableRNGs
rng = StableRNG(12)

StableRNGs.LehmerRNG(state=0x00000000000000000000000000000019)

Load the Data

To download the data visit https://doi.org/10.25739/g85n-f134 First we will load our data:

julia

obs = ehtim.obsdata.load_uvfits(joinpath(__DIR, "..", "..", "Data", "SR1_M87_2017_096_lo_hops_netcal_StokesI.uvfits"))

Python: <ehtim.obsdata.Obsdata object at 0x7faf3ae84640>

Now we do some minor preprocessing:

Scan average the data since the data have been preprocessed so that the gain phases coherent.
Add 1% systematic noise to deal with calibration issues that cause 1% non-closing errors.

julia

obs = scan_average(obs).add_fractional_noise(0.01)

Python: <ehtim.obsdata.Obsdata object at 0x7fafb20465c0>

Now we extract our complex visibilities.

julia

dvis = extract_table(obs, Visibilities())

EHTObservationTable{Comrade.EHTVisibilityDatum{:I}}
  source:      M87
  mjd:         57849
  bandwidth:   1.856e9
  sites:       [:AA, :AP, :AZ, :JC, :LM, :PV, :SM]
  nsamples:    274

##Building the Model/Posterior

Now, we must build our intensity/visibility model. That is, the model that takes in a named tuple of parameters and perhaps some metadata required to construct the model. For our model, we will use a raster or ContinuousImage for our image model. The model is given below:

The model construction is very similar to Imaging a Black Hole using only Closure Quantities, except we include a large scale gaussian since we want to model the zero baselines. For more information about the image model please read the closure-only example.

julia

function sky(θ, metadata)
    (;fg, c, σimg) = θ
    (;ftot, mimg) = metadata
    # Apply the GMRF fluctuations to the image
    rast = apply_fluctuations(CenteredLR(), mimg, σimg.*c.params)
    m = ContinuousImage((ftot*(1-fg)).*rast, BSplinePulse{3}())
    x0, y0 = centroid(m)
    # Add a large-scale gaussian to deal with the over-resolved mas flux
    g = modify(Gaussian(), Stretch(μas2rad(250.0), μas2rad(250.0)), Renormalize(ftot*fg))
    return shifted(m, -x0, -y0) + g
end

sky (generic function with 1 method)

Now, let's set up our image model. The EHT's nominal resolution is 20-25 μas. Additionally, the EHT is not very sensitive to a larger field of view. Typically 60-80 μas is enough to describe the compact flux of M87. Given this, we only need to use a small number of pixels to describe our image.

julia

npix = 32
fovx = μas2rad(150.0)
fovy = μas2rad(150.0)

7.27220521664304e-10

Now let's form our cache's. First, we have our usual image cache which is needed to numerically compute the visibilities.

julia

grid = imagepixels(fovx, fovy, npix, npix)

RectiGrid(
executor: Serial()
Dimensions: 
↓ X Sampled{Float64} LinRange{Float64}(-3.5224744018114725e-10, 3.5224744018114725e-10, 32) ForwardOrdered Regular Points,
→ Y Sampled{Float64} LinRange{Float64}(-3.5224744018114725e-10, 3.5224744018114725e-10, 32) ForwardOrdered Regular Points
)

Now we need to specify our image prior. For this work we will use a Gaussian Markov Random field prior Since we are using a Gaussian Markov random field prior we need to first specify our mean image. This behaves somewhat similary to a entropy regularizer in that it will start with an initial guess for the image structure. For this tutorial we will use a a symmetric Gaussian with a FWHM of 50 μas

julia

using VLBIImagePriors
using Distributions, DistributionsAD
fwhmfac = 2*sqrt(2*log(2))
mpr  = modify(Gaussian(), Stretch(μas2rad(50.0)./fwhmfac))
mimg = intensitymap(mpr, grid)

╭───────────────────────────────╮
│ 32×32 IntensityMap{Float64,2} │
├───────────────────────────────┴──────────────────────────────────────── dims ┐
  ↓ X Sampled{Float64} LinRange{Float64}(-3.5224744018114725e-10, 3.5224744018114725e-10, 32) ForwardOrdered Regular Points,
  → Y Sampled{Float64} LinRange{Float64}(-3.5224744018114725e-10, 3.5224744018114725e-10, 32) ForwardOrdered Regular Points
├──────────────────────────────────────────────────────────────────── metadata ┤
  ComradeBase.NoHeader()
└──────────────────────────────────────────────────────────────────────────────┘
  ↓ →          -3.52247e-10  -3.29522e-10  …  3.29522e-10  3.52247e-10
 -3.52247e-10   6.37537e-8    1.32434e-7      1.32434e-7   6.37537e-8
 -3.29522e-10   1.32434e-7    2.751e-7        2.751e-7     1.32434e-7
 -3.06796e-10   2.62014e-7    5.44273e-7      5.44273e-7   2.62014e-7
  ⋮                                        ⋱  ⋮            
  3.06796e-10   2.62014e-7    5.44273e-7      5.44273e-7   2.62014e-7
  3.29522e-10   1.32434e-7    2.751e-7        2.751e-7     1.32434e-7
  3.52247e-10   6.37537e-8    1.32434e-7      1.32434e-7   6.37537e-8

Now we can form our metadata we need to fully define our model. We will also fix the total flux to be the observed value 1.1. This is because total flux is degenerate with a global shift in the gain amplitudes making the problem degenerate. To fix this we use the observed total flux as our value.

julia

skymeta = (;ftot = 1.1, mimg = mimg./flux(mimg))

(ftot = 1.1, mimg = [6.380486931986174e-8 1.3253982629359533e-7 … 1.3253982629359533e-7 6.380486931986174e-8; 1.3253982629359533e-7 2.7532076691313077e-7 … 2.7532076691313077e-7 1.3253982629359533e-7; … ; 1.3253982629359533e-7 2.7532076691313077e-7 … 2.7532076691313077e-7 1.3253982629359533e-7; 6.380486931986174e-8 1.3253982629359533e-7 … 1.3253982629359533e-7 6.380486931986174e-8])

In addition we want a reasonable guess for what the resolution of our image should be. For radio astronomy this is given by roughly the longest baseline in the image. To put this into pixel space we then divide by the pixel size.

julia

beam = beamsize(dvis)
rat = (beam/(step(grid.X)))

5.326336637737519

To make the Gaussian Markov random field efficient we first precompute a bunch of quantities that allow us to scale things linearly with the number of image pixels. The returns a functional that accepts a single argument related to the correlation length of the field. The second argument defines the underlying random field of the Markov process. Here we are using a zero mean and unit variance Gaussian Markov random field. The keyword argument specifies the order of the Gaussian field. Currently, we recommend using order

1 which is identical to TSV variation and L₂ regularization
2 which is identical to a Matern 1 process in 2D and is really the convolution of two order 1 processes

For this tutorial we will use the first order random field

julia

crcache = ConditionalMarkov(GMRF, grid; order=1)

ConditionalMarkov(
Random Field: GaussMarkovRandomField
Graph: MarkovRandomFieldGraph{1}(
dims: (32, 32)
)
)

To demonstrate the prior let create a few random realizations

Now we can finally form our image prior. For this we use a heirarchical prior where the inverse correlation length is given by a Half-Normal distribution whose peak is at zero and standard deviation is 0.1/rat where recall rat is the beam size per pixel. For the variance of the random field we use another half normal prior with standard deviation 0.1. The reason we use the half-normal priors is to prefer "simple" structures. Gaussian Markov random fields are extremly flexible models, and to prevent overfitting it is common to use priors that penalize complexity. Therefore, we want to use priors that enforce similarity to our mean image. If the data wants more complexity then it will drive us away from the prior.

julia

cprior = HierarchicalPrior(crcache, truncated(InverseGamma(1.0, -log(0.1)*rat); upper=2*npix))

HierarchicalPrior(
	map: 
	ConditionalMarkov(
Random Field: GaussMarkovRandomField
Graph: MarkovRandomFieldGraph{1}(
dims: (32, 32)
)
)	hyper prior: 
	Truncated(Distributions.InverseGamma{Float64}(
invd: Distributions.Gamma{Float64}(α=1.0, θ=0.0815371823902832)
θ: 12.264343342322437
)
; upper=64.0)

)

We can now form our model parameter priors. Like our other imaging examples, we use a Dirichlet prior for our image pixels. For the log gain amplitudes, we use the CalPrior which automatically constructs the prior for the given jones cache gcache.

julia

prior = (
         c = cprior,
         fg = Uniform(0.0, 1.0),
         σimg = truncated(Normal(0.0, 0.1), lower=0.0)
        )

skym = SkyModel(sky, prior, grid; metadata=skymeta)

 SkyModel
  with map: sky
   on grid: RectiGrid

Unlike other imaging examples (e.g., Imaging a Black Hole using only Closure Quantities) we also need to include a model for the instrument, i.e., gains. The gains will be broken into two components

Gain amplitudes which are typically known to 10-20%, except for LMT, which has amplitudes closer to 50-100%.
Gain phases which are more difficult to constrain and can shift rapidly.

julia

G = SingleStokesGain() do x
    lg = x.lg
    gp = x.gp
    return exp(lg + 1im*gp)
end

intpr = (
    lg= ArrayPrior(IIDSitePrior(ScanSeg(), Normal(0.0, 0.2)); LM = IIDSitePrior(ScanSeg(), Normal(0.0, 1.0))),
    gp= ArrayPrior(IIDSitePrior(ScanSeg(), DiagonalVonMises(0.0, inv(π^2))); refant=SEFDReference(0.0), phase=true)
        )
intmodel = InstrumentModel(G, intpr)


post = VLBIPosterior(skym, intmodel, dvis)

VLBIPosterior
ObservedSkyModel
  with map: sky
   on grid: FourierDualDomainObservedInstrumentModel
  with Jones:  SingleStokesGain
  with reference basis: CirBasis()Data Products: Comrade.EHTVisibilityDatum

done using the asflat function.

julia

tpost = asflat(post)
ndim = dimension(tpost)

We can now also find the dimension of our posterior or the number of parameters we are going to sample.

Warning

This can often be different from what you would expect. This is especially true when using angular variables where we often artificially increase the dimension of the parameter space to make sampling easier.

To initialize our sampler we will use optimize using Adam

julia

using Optimization
using OptimizationOptimisers
using Zygote
xopt, sol = comrade_opt(post, Optimisers.Adam(), Optimization.AutoZygote(); initial_params=prior_sample(rng, post), maxiters=15_000, g_tol=1e-1)

((sky = (c = (params = [0.014796061151793164 0.030188875661724467 … 0.014507487619002267 0.007325198540498214; 0.029061310682793797 0.05926260440766695 … 0.02927150699060432 0.014791308247483037; … ; 0.06041773996842262 0.12014138381450433 … 0.10865136170811351 0.05517083397753947; 0.029971480689947694 0.05954265449067983 … 0.05340514143073982 0.027134747901529987], hyperparams = 18.960022742504048), fg = 0.20824015870155774, σimg = 1.0537454603589058), instrument = (lg = [0.04785250082730885, 0.04784969130154198, 0.011362385050966789, 0.024897603536498822, -0.38508958463071785, 0.16878373459020332, 0.00657987658047647, 0.028805022303884924, -0.22105930956230835, 0.12747730111253577  …  -0.21294948760828217, 0.01723378662999891, -0.9245830247469357, 0.015344820504667931, 0.00943670366637407, 0.02675794080082609, -0.27199619555536914, 0.01795183848202046, -0.9742043027372719, 0.01479432895570256], gp = [0.0, -2.6817163206890835, 0.0, -2.1743323023314454, -0.10053464023508142, -2.8928364046479764, 0.0, -2.2305553200746755, -0.039000334534607016, -3.129002024054032  …  -3.4303665126228315, -0.7582745636957844, -4.115711204580517, 2.4026814284792612, 0.0, -1.827318377155086, -3.5493543806425194, -0.7117852425691287, -4.264310120680278, 2.451632190572669])), retcode: Default
u: [0.014796061151793164, 0.029061310682793797, 0.042282378472289536, 0.05397764140892939, 0.06368314717983126, 0.07102450533601626, 0.07587819959001633, 0.07850985257638007, 0.0794990953199291, 0.0795034436583845  …  0.05881599917915929, 0.9375795699435095, -0.11151335259551606, 0.9327554494757166, 0.0436560271995193, 0.9383783410615553, -0.1390872471782709, 0.9290914258810878, 0.045964992501015205, 0.9382545081992535]
Final objective value:     -1626.747180412683
)

Warning

Fitting gains tends to be very difficult, meaning that optimization can take a lot longer. The upside is that we usually get nicer images.

First we will evaluate our fit by plotting the residuals

julia

using Plots
using DisplayAs
residual(post, xopt) |> DisplayAs.PNG |> DisplayAs.Text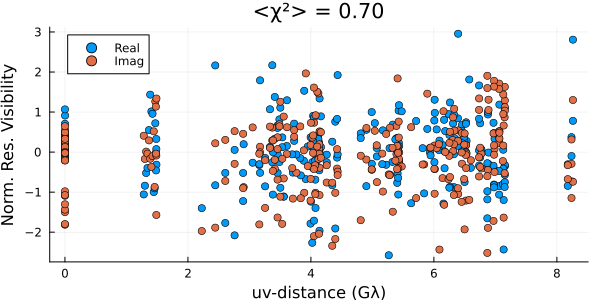

These look reasonable, although there may be some minor overfitting. This could be improved in a few ways, but that is beyond the goal of this quick tutorial. Plotting the image, we see that we have a much cleaner version of the closure-only image from Imaging a Black Hole using only Closure Quantities.

julia

import CairoMakie as CM
g = imagepixels(fovx, fovy, 128, 128)
img = intensitymap(skymodel(post, xopt), g)
imageviz(img, size=(500, 400))|> DisplayAs.PNG |> DisplayAs.Text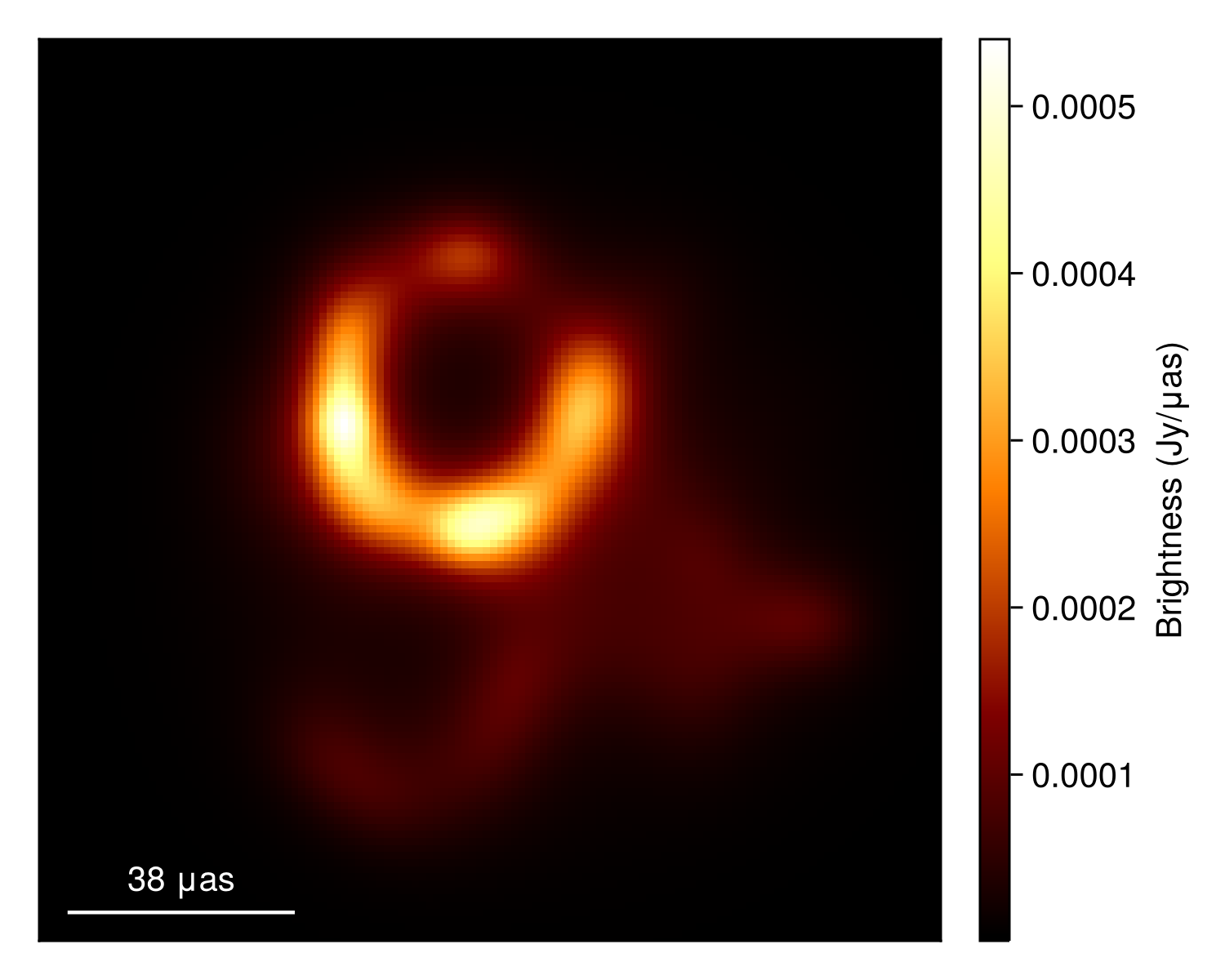

Because we also fit the instrument model, we can inspect their parameters. To do this, Comrade provides a caltable function that converts the flattened gain parameters to a tabular format based on the time and its segmentation.

julia

gt = Comrade.caltable(xopt.instrument.gp)
plot(gt, layout=(3,3), size=(600,500)) |> DisplayAs.PNG |> DisplayAs.Text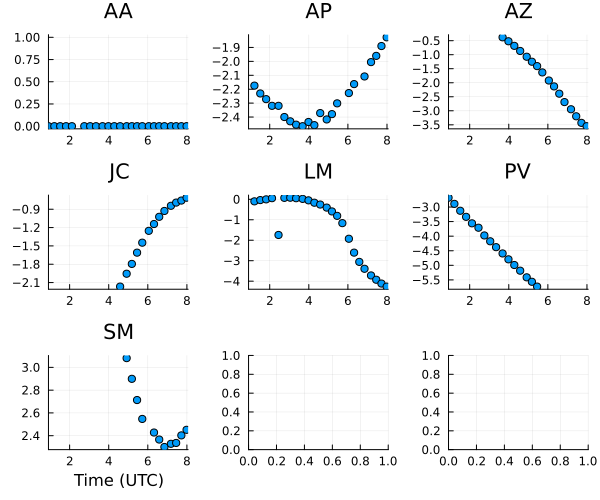

The gain phases are pretty random, although much of this is due to us picking a random reference sites for each scan.

Moving onto the gain amplitudes, we see that most of the gain variation is within 10% as expected except LMT, which has massive variations.

julia

gt = Comrade.caltable(exp.(xopt.instrument.lg))
plot(gt, layout=(3,3), size=(600,500)) |> DisplayAs.PNG |> DisplayAs.Text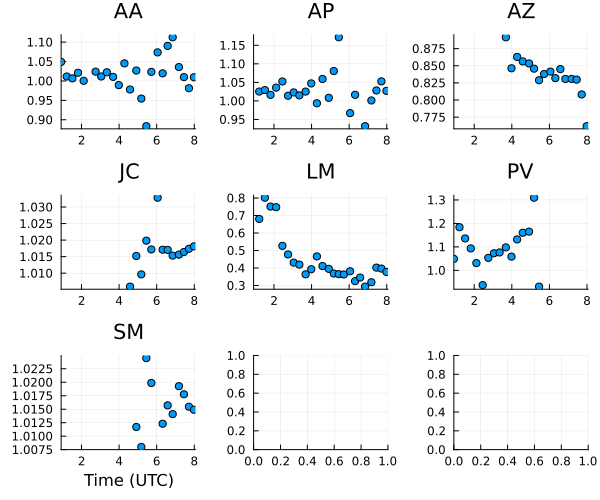

To sample from the posterior, we will use HMC, specifically the NUTS algorithm. For information about NUTS, see Michael Betancourt's notes. However, due to the need to sample a large number of gain parameters, constructing the posterior is rather time-consuming. Therefore, for this tutorial, we will only do a quick preliminary run

julia

using AdvancedHMC
chain = sample(rng, post, NUTS(0.8), 700; n_adapts=500, progress=false, initial_params=xopt)

PosteriorSamples
  Samples size: (700,)
  sampler used: AHMC
Mean
┌───────────────────────────────────────────────────────────────────────────────
│ sky                                                                          ⋯
│ @NamedTuple{c::@NamedTuple{params::Matrix{Float64}, hyperparams::Float64}, f ⋯
├───────────────────────────────────────────────────────────────────────────────
│ (c = (params = [0.079576 0.0806425 … -0.00849204 -0.0617906; 0.0828325 0.178 ⋯
└───────────────────────────────────────────────────────────────────────────────
                                                               2 columns omitted
Std. Dev.
┌───────────────────────────────────────────────────────────────────────────────
│ sky                                                                          ⋯
│ @NamedTuple{c::@NamedTuple{params::Matrix{Float64}, hyperparams::Float64}, f ⋯
├───────────────────────────────────────────────────────────────────────────────
│ (c = (params = [0.521147 0.582224 … 0.584762 0.565177; 0.592423 0.650033 … 0 ⋯
└───────────────────────────────────────────────────────────────────────────────
                                                               2 columns omitted

Note

The above sampler will store the samples in memory, i.e. RAM. For large models this can lead to out-of-memory issues. To fix that you can include the keyword argument saveto = DiskStore() which periodically saves the samples to disk limiting memory useage. You can load the chain using load_samples(diskout) where diskout is the object returned from sample.

Now we prune the adaptation phase

julia

chain = chain[501:end]

PosteriorSamples
  Samples size: (200,)
  sampler used: AHMC
Mean
┌───────────────────────────────────────────────────────────────────────────────
│ sky                                                                          ⋯
│ @NamedTuple{c::@NamedTuple{params::Matrix{Float64}, hyperparams::Float64}, f ⋯
├───────────────────────────────────────────────────────────────────────────────
│ (c = (params = [-0.00911847 -0.000575872 … -0.0698193 -0.104049; -0.0206791  ⋯
└───────────────────────────────────────────────────────────────────────────────
                                                               2 columns omitted
Std. Dev.
┌───────────────────────────────────────────────────────────────────────────────
│ sky                                                                          ⋯
│ @NamedTuple{c::@NamedTuple{params::Matrix{Float64}, hyperparams::Float64}, f ⋯
├───────────────────────────────────────────────────────────────────────────────
│ (c = (params = [0.489445 0.600709 … 0.534011 0.542165; 0.583052 0.592202 … 0 ⋯
└───────────────────────────────────────────────────────────────────────────────
                                                               2 columns omitted

Warning

This should be run for likely an order of magnitude more steps to properly estimate expectations of the posterior

Now that we have our posterior, we can put error bars on all of our plots above. Let's start by finding the mean and standard deviation of the gain phases

julia

mchain = Comrade.rmap(mean, chain)
schain = Comrade.rmap(std, chain)

(sky = (c = (params = [0.48944519445233614 0.6007087907042052 … 0.5340107406147621 0.5421645830753561; 0.5830524068886781 0.5922021028300926 … 0.6477864038931529 0.5798025280705609; … ; 0.5102166191068493 0.6801297315121118 … 0.6517016053732577 0.575386757647284; 0.579508461377615 0.5979373623871471 … 0.6578933172601547 0.5497513431999317], hyperparams = 13.588165729782826), fg = 0.043428131295733016, σimg = 0.04836349454711231), instrument = (lg = [0.141048661942198, 0.13886653614349004, 0.0160296947670061, 0.016667801836268255, 0.05931964699454964, 0.0498814627157853, 0.014754008429668451, 0.015016645337856526, 0.05211173454508231, 0.04664822303858821  …  0.03646227855126081, 0.010755022107477094, 0.04423893049838281, 0.009803247818187555, 0.013712540550607675, 0.015652668812330746, 0.03779689618601689, 0.011138390854574722, 0.047327069169462416, 0.011097102821106533], gp = [0.0, 0.2754324195841769, 0.0, 0.009420203520614697, 0.20000675644304453, 0.2784572457712028, 0.0, 0.010592745040641683, 0.20594737505898167, 0.2844227584940223  …  0.2459376473354253, 0.2818412550798841, 0.22345661589853727, 0.2831421544378363, 0.0, 0.010155921439509526, 0.24258951980980167, 0.28162898507358336, 0.21760630912315418, 0.280691495595419]))

Now we can use the measurements package to automatically plot everything with error bars. First we create a caltable the same way but making sure all of our variables have errors attached to them.

julia

using Measurements
gmeas_am = Measurements.measurement.(mchain.instrument.lg, schain.instrument.lg)
ctable_am = caltable(exp.(gmeas_am)) # caltable expects gmeas_am to be a Vector
gmeas_ph = Measurements.measurement.(mchain.instrument.gp, schain.instrument.gp)
ctable_ph = caltable(gmeas_ph)

───────────────────────────────────────────────────┬────────────────────────────
                                              time │      AA              AP   ⋯
───────────────────────────────────────────────────┼────────────────────────────
 IntegrationTime{Float64}(57849, 0.916667, 0.0002) │ 0.0±0.0         missing   ⋯
  IntegrationTime{Float64}(57849, 1.21667, 0.0002) │ 0.0±0.0  -2.1748±0.0094   ⋯
  IntegrationTime{Float64}(57849, 1.51667, 0.0002) │ 0.0±0.0     -2.23±0.011   ⋯
  IntegrationTime{Float64}(57849, 1.81667, 0.0002) │ 0.0±0.0  -2.2714±0.0093   ⋯
  IntegrationTime{Float64}(57849, 2.11667, 0.0002) │ 0.0±0.0  -2.3184±0.0097   ⋯
     IntegrationTime{Float64}(57849, 2.45, 0.0002) │ missing  -2.3184±0.0097   ⋯
     IntegrationTime{Float64}(57849, 2.75, 0.0002) │ 0.0±0.0       -2.4±0.01   ⋯
     IntegrationTime{Float64}(57849, 3.05, 0.0002) │ 0.0±0.0     -2.431±0.01   ⋯
     IntegrationTime{Float64}(57849, 3.35, 0.0002) │ 0.0±0.0     -2.454±0.01   ⋯
  IntegrationTime{Float64}(57849, 3.68333, 0.0002) │ 0.0±0.0  -2.4656±0.0095   ⋯
  IntegrationTime{Float64}(57849, 3.98333, 0.0002) │ 0.0±0.0  -2.4363±0.0096   ⋯
  IntegrationTime{Float64}(57849, 4.28333, 0.0002) │ 0.0±0.0    -2.457±0.011   ⋯
  IntegrationTime{Float64}(57849, 4.58333, 0.0002) │ 0.0±0.0    -2.372±0.011   ⋯
  IntegrationTime{Float64}(57849, 4.91667, 0.0002) │ 0.0±0.0     -2.416±0.01   ⋯
  IntegrationTime{Float64}(57849, 5.18333, 0.0002) │ 0.0±0.0  -2.3787±0.0096   ⋯
     IntegrationTime{Float64}(57849, 5.45, 0.0002) │ 0.0±0.0  -2.3019±0.0098   ⋯
                         ⋮                         │    ⋮           ⋮          ⋱
───────────────────────────────────────────────────┴────────────────────────────
                                                    5 columns and 9 rows omitted

Now let's plot the phase curves

julia

plot(ctable_ph, layout=(3,3), size=(600,500)) |> DisplayAs.PNG |> DisplayAs.Text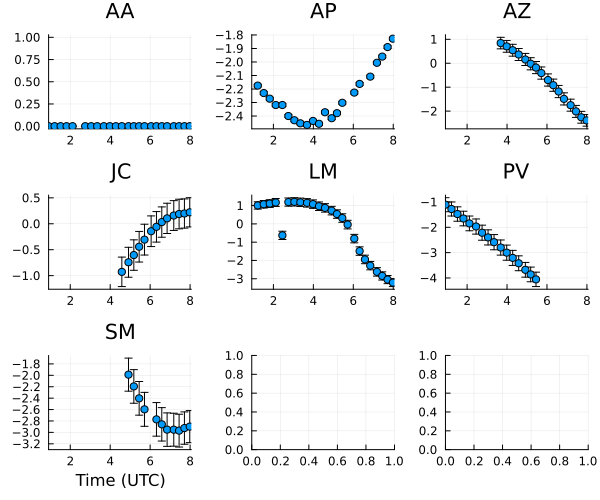

and now the amplitude curves

julia

plot(ctable_am, layout=(3,3), size=(600,500)) |> DisplayAs.PNG |> DisplayAs.Text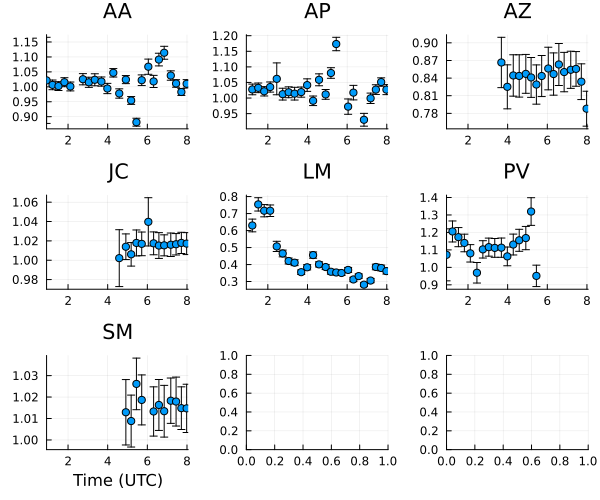

Finally let's construct some representative image reconstructions.

julia

samples = skymodel.(Ref(post), chain[begin:2:end])
imgs = intensitymap.(samples, Ref(g))

mimg = mean(imgs)
simg = std(imgs)
fig = CM.Figure(;resolution=(700, 700));
axs = [CM.Axis(fig[i, j], xreversed=true, aspect=1) for i in 1:2, j in 1:2]
CM.image!(axs[1,1], mimg, colormap=:afmhot); axs[1, 1].title="Mean"
CM.image!(axs[1,2], simg./(max.(mimg, 1e-8)), colorrange=(0.0, 2.0), colormap=:afmhot);axs[1,2].title = "Std"
CM.image!(axs[2,1], imgs[1],   colormap=:afmhot);
CM.image!(axs[2,2], imgs[end], colormap=:afmhot);
CM.hidedecorations!.(axs)
fig |> DisplayAs.PNG |> DisplayAs.Text

And viola, you have just finished making a preliminary image and instrument model reconstruction. In reality, you should run the sample step for many more MCMC steps to get a reliable estimate for the reconstructed image and instrument model parameters.

This page was generated using Literate.jl.

Stokes I Simultaneous Image and Instrument Modeling ​

Load the Data ​

Stokes I Simultaneous Image and Instrument Modeling

Load the Data