Polarized Image and Instrumental Modeling

In this tutorial, we will analyze a simulated simple polarized dataset to demonstrate Comrade's polarized imaging capabilities.

Introduction to Polarized Imaging

The EHT is a polarized interferometer. However, like all VLBI interferometers, it does not directly measure the Stokes parameters (I, Q, U, V). Instead, it measures components related to the electric field at the telescope along two directions using feeds. There are two types of feeds at telescopes: circular, which measure $R / L$ components of the electric field, and linear feeds, which measure $X / Y$ components of the electric field. Most sites in the EHT use circular feeds, meaning they measure the right (R) and left electric field (L) at each telescope. Although note that ALMA actually uses linear feeds. Currently Comrade has the ability to fit natively mixed polarization data however, the publically released EHT data has been converted to circular polarization. For a VLBI array whose feeds are purely circluar the coherency matrices are given by,

C_{i j} = (\begin{matrix} R R^{*} & R L^{*} \\ L R^{*} & L L^{*} \end{matrix}) .

These coherency matrices are the fundamental object in interferometry and what the telescope observes. For a perfect interferometer, these circular coherency matrices are related to the usual Fourier transform of the stokes parameters by

(\begin{matrix} \tilde{I} \\ \tilde{Q} \\ \tilde{U} \\ \tilde{V} \end{matrix}) = \frac{1}{2} (\begin{matrix} R R^{*} + L L^{*} \\ R L^{*} + L R^{*} \\ i (L R^{*} - R L^{*}) \\ R R^{*} - L L^{*} \end{matrix}) .

Note

In this tutorial, we stick to circular feeds but Comrade has the capabilities to model linear (XX,XY, ...) and mixed basis coherencies (e.g., RX, RY, ...).

In reality, the measure coherencies are corrupted by both the atmosphere and the telescope itself. In Comrade we use the RIME formalism ^[1] to represent these corruptions, namely our measured coherency matrices $V_{i j}$ are given by

V_{i j} = J_{i} C_{i j} J_{j}^{†}

where $J$ is known as a Jones matrix and $i j$ denotes the baseline $i j$ with sites $i$ and $j$ .

Comrade is highly flexible with how the Jones matrices are formed and provides several convenience functions that parameterize standard Jones matrices. These matrices include:

JonesG which builds the set of complex gain Jones matrices

G = (\begin{matrix} g_{a} & 0 \\ 0 & g_{b} \end{matrix})

JonesD which builds the set of complex d-terms Jones matrices

D = (\begin{matrix} 1 & d_{a} \\ d_{b} & 1 \end{matrix})

JonesR is the ideal telescope response $R$ . This transformation is special and combines two things using the decomposition $R = F B$ . The first, $B$ , is the transformation from some reference basis to the observed coherency basis (this allows for mixed basis measurements). The second is the feed rotation, $F$ , that transforms from some reference axis to the axis of the telescope as the source moves in the sky. The feed rotation matrix F for circular feeds in terms of the per station feed rotation angle $φ$ is

F = (\begin{matrix} e^{- i φ} & 0 \\ 0 & e^{i φ} \end{matrix})

In the rest of the tutorial, we are going to solve for all of these instrument model terms in while re-creating the polarized image from the first EHT results on M87.

Load the Data

To get started we will load Comrade

julia

using Comrade

Load the Data

julia

using Pyehtim

    CondaPkg Found dependencies: /home/runner/.julia/packages/CondaPkg/8GjrP/CondaPkg.toml
    CondaPkg Found dependencies: /home/runner/.julia/packages/PythonCall/83z4q/CondaPkg.toml
    CondaPkg Found dependencies: /home/runner/.julia/packages/Pyehtim/bQtHC/CondaPkg.toml
    CondaPkg Resolving changes
             + ehtim (pip)
             + libstdcxx
             + libstdcxx-ng
             + numpy
             + numpy (pip)
             + openssl
             + pandas
             + python
             + setuptools (pip)
             + uv
    CondaPkg Initialising pixi
             │ /home/runner/.julia/artifacts/cefba4912c2b400756d043a2563ef77a0088866b/bin/pixi
             │ init
             │ --format pixi
             └ /home/runner/work/Comrade.jl/Comrade.jl/examples/intermediate/PolarizedImaging/.CondaPkg
✔ Created /home/runner/work/Comrade.jl/Comrade.jl/examples/intermediate/PolarizedImaging/.CondaPkg/pixi.toml
    CondaPkg Wrote /home/runner/work/Comrade.jl/Comrade.jl/examples/intermediate/PolarizedImaging/.CondaPkg/pixi.toml
             │ [dependencies]
             │ openssl = ">=3, <3.6"
             │ libstdcxx = ">=3.4,<15.0"
             │ uv = ">=0.4"
             │ libstdcxx-ng = ">=3.4,<15.0"
             │ pandas = "<2"
             │ numpy = ">=1.24, <2.0"
             │ 
             │     [dependencies.python]
             │     channel = "conda-forge"
             │     build = "*cp*"
             │     version = ">=3.10,!=3.14.0,!=3.14.1,<4, >=3.6,<=3.12"
             │ 
             │ [project]
             │ name = ".CondaPkg"
             │ platforms = ["linux-64"]
             │ channels = ["conda-forge"]
             │ channel-priority = "strict"
             │ description = "automatically generated by CondaPkg.jl"
             │ 
             │ [pypi-dependencies]
             │ ehtim = ">=1.2.10, <2.0"
             │ numpy = ">=1.24, <2.0"
             └ setuptools = "*"
    CondaPkg Installing packages
             │ /home/runner/.julia/artifacts/cefba4912c2b400756d043a2563ef77a0088866b/bin/pixi
             │ install
             └ --manifest-path /home/runner/work/Comrade.jl/Comrade.jl/examples/intermediate/PolarizedImaging/.CondaPkg/pixi.toml
✔ The default environment has been installed.

For reproducibility we use a stable random number genreator

julia

using StableRNGs
rng = StableRNG(48)

StableRNGs.LehmerRNG(state=0x00000000000000000000000000000061)

Now we will load some synthetic polarized data.

julia

fname = Base.download(
    "https://de.cyverse.org/anon-files/iplant/home/shared/commons_repo/curated/EHTC_M87pol2017_Nov2023/hops_data/April11/SR2_M87_2017_101_lo_hops_ALMArot.uvfits",
    joinpath(__DIR, "m87polarized.uvfits")
)
obs = Pyehtim.load_uvfits_and_array(
    fname,
    joinpath(__DIR, "..", "..", "Data", "array.txt"), polrep = "circ"
)

Python: <ehtim.obsdata.Obsdata object at 0x7fd9f9a8e7d0>

Notice that, unlike other non-polarized tutorials, we need to include a second argument. This is the array file of the observation and is required to determine the feed rotation of the array.

Now we scan average the data since the data to boost the SNR and reduce the total data volume.

julia

obs = scan_average(obs).add_fractional_noise(0.01).flag_uvdist(uv_min = 0.1e9)

Python: <ehtim.obsdata.Obsdata object at 0x7fd9f4747610>

Now we extract our observed/corrupted coherency matrices.

julia

dvis = extract_table(obs, Coherencies())

EHTObservationTable{Comrade.EHTCoherencyDatum{Float64}}
  source:      M87
  mjd:         57854
  bandwidth:   1.856e9
  sites:       [:AA, :AP, :AZ, :JC, :LM, :PV, :SM]
  nsamples:    189

##Building the Model/Posterior

To build the model, we first break it down into two parts:

The image or sky model. In Comrade, all polarized image models are written in terms of the Stokes parameters. In this tutorial, we will use a polarized image model based on Pesce (2021)^[2], and parameterizes each pixel in terms of the Poincare sphere. This parameterization ensures that we have all the physical properties of stokes parameters. Note that we also have a parameterization in terms of hyperbolic trig functions VLBISkyModels.PolExp2Map
The instrument model. The instrument model specifies the model that describes the impact of instrumental and atmospheric effects. We will be using the $J = G D R$ decomposition we described above. However, to parameterize the R/L complex gains, we will be using a gain product and ratio decomposition. The reason for this decomposition is that in realistic measurements, the gain ratios and products have different temporal characteristics. Namely, many of the EHT observations tend to demonstrate constant R/L gain ratios across an nights observations, compared to the gain products, which vary every scan. Additionally, the gain ratios tend to be smaller (i.e., closer to unity) than the gain products. Using this apriori knowledge, we can build this into our model and reduce the total number of parameters we need to model.

First we specify our sky model. As always Comrade requires this to be a two argument function where the first argument is typically a NamedTuple of parameters we will fit and the second are additional metadata required to build the model.

julia

function sky(θ, metadata)
    (; σs, as) = θ
    (; mimg, ftot) = metadata
    # Build the stokes I model
    δs = ntuple(Val(4)) do i
        σs[i] * as[i].params
    end

    # Convert hyperbolic polarization basis to Stokes basis
    pmap = VLBISkyModels.PolExp2Map!(δs..., axisdims(mimg))

    # We now add a mean image. Namely, we assume that `pmap` are multiplicative fluctuations
    # about some mean image `mimg`. We also compute the total flux of the Stokes I image
    # for normalization purposes below.
    ft = zero(eltype(mimg))
    for i in eachindex(pmap, mimg)
        pmap[i] *= mimg[i]
        ft += pmap[i].I
    end

    pmap .= ftot .* pmap ./ ft
    m = ContinuousImage(pmap, BSplinePulse{3}())
    x, y = centroid(pmap)
    return shifted(m, -x, -y)
end

sky (generic function with 1 method)

Now, we define the model metadata required to build the model. We specify our image grid and cache model needed to define the polarimetric image model. Our image will be a 10x10 raster with a 60μas FOV.

julia

using Distributions
using VLBIImagePriors
fovx = μas2rad(200.0)
fovy = μas2rad(200.0)
nx = ny = 48
grid = imagepixels(fovx, fovy, nx, ny)

fwhmfac = 2 * sqrt(2 * log(2))
mpr = modify(Gaussian(), Stretch(μas2rad(50.0) ./ fwhmfac))
mimg = intensitymap(mpr, grid)

┌ 48×48 IntensityMap{Float64, 2} ┐
├────────────────────────────────┴─────────────────────────────────────── dims ┐
  ↓ X Sampled{Float64} LinRange{Float64}(-4.747133960864206e-10, 4.747133960864206e-10, 48) ForwardOrdered Regular Points,
  → Y Sampled{Float64} LinRange{Float64}(-4.747133960864206e-10, 4.747133960864206e-10, 48) ForwardOrdered Regular Points
└──────────────────────────────────────────────────────────────────────────────┘
  ↓ →          -4.74713e-10  -4.54513e-10  -4.34312e-10  -4.14112e-10  -3.93911e-10  -3.73711e-10  -3.5351e-10   -3.33309e-10  -3.13109e-10  -2.92908e-10  -2.72708e-10  -2.52507e-10  -2.32307e-10  -2.12106e-10  -1.91905e-10  -1.71705e-10  -1.51504e-10  -1.31304e-10  -1.11103e-10  -9.09026e-11  -7.0702e-11   -5.05014e-11  -3.03009e-11  -1.01003e-11  1.01003e-11  3.03009e-11  5.05014e-11  7.0702e-11   9.09026e-11  1.11103e-10  1.31304e-10  1.51504e-10  1.71705e-10  1.91905e-10  2.12106e-10  2.32307e-10  2.52507e-10  2.72708e-10  2.92908e-10  3.13109e-10  3.33309e-10  3.5351e-10   3.73711e-10  3.93911e-10  4.14112e-10  4.34312e-10  4.54513e-10  4.74713e-10
 -4.74713e-10   0.0           0.0           0.0           0.0           9.76922e-11   2.03055e-10   4.0611e-10    7.81538e-10   1.44721e-9    2.57864e-9    4.42105e-9    7.29349e-9    1.15777e-8    1.76842e-8    2.59911e-8    3.67569e-8    5.00184e-8    6.54933e-8    8.25164e-8    1.00037e-7    1.16696e-7    1.30987e-7    1.41473e-7    1.47028e-7   1.47028e-7   1.41473e-7   1.30987e-7   1.16696e-7   1.00037e-7   8.25164e-8   6.54933e-8   5.00184e-8   3.67569e-8   2.59911e-8   1.76842e-8   1.15777e-8   7.29349e-9   4.42105e-9   2.57864e-9   1.44721e-9   7.81538e-10  4.0611e-10   2.03055e-10  9.76922e-11  0.0          0.0          0.0          0.0
 -4.54513e-10   0.0           0.0           0.0           1.09656e-10   2.3687e-10    4.92338e-10   9.84676e-10   1.89496e-9    3.50899e-9    6.2523e-9     1.07195e-8    1.76842e-8    2.80719e-8    4.2878e-8     6.30193e-8    8.91227e-8    1.21277e-7    1.58799e-7    2.00074e-7    2.42555e-7    2.82947e-7    3.17597e-7    3.43024e-7    3.56491e-7   3.56491e-7   3.43024e-7   3.17597e-7   2.82947e-7   2.42555e-7   2.00074e-7   1.58799e-7   1.21277e-7   8.91227e-8   6.30193e-8   4.2878e-8    2.80719e-8   1.76842e-8   1.07195e-8   6.2523e-9    3.50899e-9   1.89496e-9   9.84676e-10  4.92338e-10  2.3687e-10   1.09656e-10  0.0          0.0          0.0
 -4.34312e-10   0.0           0.0           1.13961e-10   2.55833e-10   5.52631e-10   1.14865e-9    2.29731e-9    4.42105e-9    8.18667e-9    1.4587e-8     2.50092e-8    4.12582e-8    6.54933e-8    1.00037e-7    1.47028e-7    2.07928e-7    2.82947e-7    3.70486e-7    4.66784e-7    5.65894e-7    6.60132e-7    7.40973e-7    8.00295e-7    8.31714e-7   8.31714e-7   8.00295e-7   7.40973e-7   6.60132e-7   5.65894e-7   4.66784e-7   3.70486e-7   2.82947e-7   2.07928e-7   1.47028e-7   1.00037e-7   6.54933e-8   4.12582e-8   2.50092e-8   1.4587e-8    8.18667e-9   4.42105e-9   2.29731e-9   1.14865e-9   5.52631e-10  2.55833e-10  1.13961e-10  0.0          0.0
 -4.14112e-10   0.0           1.09656e-10   2.55833e-10   5.74327e-10   1.24061e-9    2.57864e-9    5.15728e-9    9.92491e-9    1.83784e-8    3.27467e-8    5.61438e-8    9.26216e-8    1.47028e-7    2.24575e-7    3.30066e-7    4.66784e-7    6.35194e-7    8.31714e-7    1.04789e-6    1.27039e-6    1.48195e-6    1.66343e-6    1.7966e-6     1.86713e-6   1.86713e-6   1.7966e-6    1.66343e-6   1.48195e-6   1.27039e-6   1.04789e-6   8.31714e-7   6.35194e-7   4.66784e-7   3.30066e-7   2.24575e-7   1.47028e-7   9.26216e-8   5.61438e-8   3.27467e-8   1.83784e-8   9.92491e-9   5.15728e-9   2.57864e-9   1.24061e-9   5.74327e-10  2.55833e-10  1.09656e-10  0.0
 -3.93911e-10   9.76922e-11   2.3687e-10    5.52631e-10   1.24061e-9    2.67987e-9    5.57017e-9    1.11403e-8    2.1439e-8     3.96996e-8    7.07367e-8    1.21277e-7    2.00074e-7    3.17597e-7    4.85109e-7    7.12982e-7    1.00831e-6    1.3721e-6     1.7966e-6     2.26358e-6    2.74419e-6    3.20118e-6    3.5932e-6     3.88087e-6    4.03323e-6   4.03323e-6   3.88087e-6   3.5932e-6    3.20118e-6   2.74419e-6   2.26358e-6   1.7966e-6    1.3721e-6    1.00831e-6   7.12982e-7   4.85109e-7   3.17597e-7   2.00074e-7   1.21277e-7   7.07367e-8   3.96996e-8   2.1439e-8    1.11403e-8   5.57017e-9   2.67987e-9   1.24061e-9   5.52631e-10  2.3687e-10   9.76922e-11
 -3.73711e-10   2.03055e-10   4.92338e-10   1.14865e-9    2.57864e-9    5.57017e-9    1.15777e-8    2.31554e-8    4.45613e-8    8.25164e-8    1.47028e-7    2.52077e-7    4.15857e-7    6.60132e-7    1.00831e-6    1.48195e-6    2.09579e-6    2.85193e-6    3.73427e-6    4.70488e-6    5.70385e-6    6.65371e-6    7.46854e-6    8.06647e-6    8.38315e-6   8.38315e-6   8.06647e-6   7.46854e-6   6.65371e-6   5.70385e-6   4.70488e-6   3.73427e-6   2.85193e-6   2.09579e-6   1.48195e-6   1.00831e-6   6.60132e-7   4.15857e-7   2.52077e-7   1.47028e-7   8.25164e-8   4.45613e-8   2.31554e-8   1.15777e-8   5.57017e-9   2.57864e-9   1.14865e-9   4.92338e-10  2.03055e-10
 -3.5351e-10    4.0611e-10    9.84676e-10   2.29731e-9    5.15728e-9    1.11403e-8    2.31554e-8    4.63108e-8    8.91227e-8    1.65033e-7    2.94055e-7    5.04154e-7    8.31714e-7    1.32026e-6    2.01662e-6    2.96389e-6    4.19157e-6    5.70385e-6    7.46854e-6    9.40977e-6    1.14077e-5    1.33074e-5    1.49371e-5    1.61329e-5    1.67663e-5   1.67663e-5   1.61329e-5   1.49371e-5   1.33074e-5   1.14077e-5   9.40977e-6   7.46854e-6   5.70385e-6   4.19157e-6   2.96389e-6   2.01662e-6   1.32026e-6   8.31714e-7   5.04154e-7   2.94055e-7   1.65033e-7   8.91227e-8   4.63108e-8   2.31554e-8   1.11403e-8   5.15728e-9   2.29731e-9   9.84676e-10  4.0611e-10
 -3.33309e-10   7.81538e-10   1.89496e-9    4.42105e-9    9.92491e-9    2.1439e-8     4.45613e-8    8.91227e-8    1.71512e-7    3.17597e-7    5.65894e-7    9.70218e-7    1.60059e-6    2.54078e-6    3.88087e-6    5.70385e-6    8.06647e-6    1.09768e-5    1.43728e-5    1.81086e-5    2.19535e-5    2.56094e-5    2.87456e-5    3.1047e-5     3.22659e-5   3.22659e-5   3.1047e-5    2.87456e-5   2.56094e-5   2.19535e-5   1.81086e-5   1.43728e-5   1.09768e-5   8.06647e-6   5.70385e-6   3.88087e-6   2.54078e-6   1.60059e-6   9.70218e-7   5.65894e-7   3.17597e-7   1.71512e-7   8.91227e-8   4.45613e-8   2.1439e-8    9.92491e-9   4.42105e-9   1.89496e-9   7.81538e-10
 -3.13109e-10   1.44721e-9    3.50899e-9    8.18667e-9    1.83784e-8    3.96996e-8    8.25164e-8    1.65033e-7    3.17597e-7    5.8811e-7     1.04789e-6    1.7966e-6     2.96389e-6    4.70488e-6    7.1864e-6     1.05621e-5    1.49371e-5    2.03262e-5    2.66148e-5    3.35326e-5    4.06524e-5    4.74222e-5    5.32297e-5    5.74912e-5    5.97483e-5   5.97483e-5   5.74912e-5   5.32297e-5   4.74222e-5   4.06524e-5   3.35326e-5   2.66148e-5   2.03262e-5   1.49371e-5   1.05621e-5   7.1864e-6    4.70488e-6   2.96389e-6   1.7966e-6    1.04789e-6   5.8811e-7    3.17597e-7   1.65033e-7   8.25164e-8   3.96996e-8   1.83784e-8   8.18667e-9   3.50899e-9   1.44721e-9
 -2.92908e-10   2.57864e-9    6.2523e-9     1.4587e-8     3.27467e-8    7.07367e-8    1.47028e-7    2.94055e-7    5.65894e-7    1.04789e-6    1.86713e-6    3.20118e-6    5.28105e-6    8.38315e-6    1.28047e-5    1.88195e-5    2.66148e-5    3.62172e-5    4.74222e-5    5.97483e-5    7.24344e-5    8.44968e-5    9.48445e-5    0.000102438   0.000106459  0.000106459  0.000102438  9.48445e-5   8.44968e-5   7.24344e-5   5.97483e-5   4.74222e-5   3.62172e-5   2.66148e-5   1.88195e-5   1.28047e-5   8.38315e-6   5.28105e-6   3.20118e-6   1.86713e-6   1.04789e-6   5.65894e-7   2.94055e-7   1.47028e-7   7.07367e-8   3.27467e-8   1.4587e-8    6.2523e-9    2.57864e-9
 -2.72708e-10   4.42105e-9    1.07195e-8    2.50092e-8    5.61438e-8    1.21277e-7    2.52077e-7    5.04154e-7    9.70218e-7    1.7966e-6     3.20118e-6    5.48838e-6    9.0543e-6     1.43728e-5    2.19535e-5    3.22659e-5    4.56308e-5    6.2094e-5     8.13049e-5    0.000102438   0.000124188   0.000144869   0.00016261    0.000175628   0.000182523  0.000182523  0.000175628  0.00016261   0.000144869  0.000124188  0.000102438  8.13049e-5   6.2094e-5    4.56308e-5   3.22659e-5   2.19535e-5   1.43728e-5   9.0543e-6    5.48838e-6   3.20118e-6   1.7966e-6    9.70218e-7   5.04154e-7   2.52077e-7   1.21277e-7   5.61438e-8   2.50092e-8   1.07195e-8   4.42105e-9
 -2.52507e-10   7.29349e-9    1.76842e-8    4.12582e-8    9.26216e-8    2.00074e-7    4.15857e-7    8.31714e-7    1.60059e-6    2.96389e-6    5.28105e-6    9.0543e-6     1.49371e-5    2.37111e-5    3.62172e-5    5.32297e-5    7.52781e-5    0.000102438   0.00013413    0.000168994   0.000204875   0.000238993   0.000268261   0.000289738   0.000301113  0.000301113  0.000289738  0.000268261  0.000238993  0.000204875  0.000168994  0.00013413   0.000102438  7.52781e-5   5.32297e-5   3.62172e-5   2.37111e-5   1.49371e-5   9.0543e-6    5.28105e-6   2.96389e-6   1.60059e-6   8.31714e-7   4.15857e-7   2.00074e-7   9.26216e-8   4.12582e-8   1.76842e-8   7.29349e-9
 -2.32307e-10   1.15777e-8    2.80719e-8    6.54933e-8    1.47028e-7    3.17597e-7    6.60132e-7    1.32026e-6    2.54078e-6    4.70488e-6    8.38315e-6    1.43728e-5    2.37111e-5    3.76391e-5    5.74912e-5    8.44968e-5    0.000119497   0.00016261    0.000212919   0.000268261   0.00032522    0.000379378   0.000425837   0.00045993    0.000477986  0.000477986  0.00045993   0.000425837  0.000379378  0.00032522   0.000268261  0.000212919  0.00016261   0.000119497  8.44968e-5   5.74912e-5   3.76391e-5   2.37111e-5   1.43728e-5   8.38315e-6   4.70488e-6   2.54078e-6   1.32026e-6   6.60132e-7   3.17597e-7   1.47028e-7   6.54933e-8   2.80719e-8   1.15777e-8
 -2.12106e-10   1.76842e-8    4.2878e-8     1.00037e-7    2.24575e-7    4.85109e-7    1.00831e-6    2.01662e-6    3.88087e-6    7.1864e-6     1.28047e-5    2.19535e-5    3.62172e-5    5.74912e-5    8.78141e-5    0.000129063   0.000182523   0.000248376   0.00032522    0.000409751   0.000496752   0.000579475   0.000650439   0.000702513   0.000730093  0.000730093  0.000702513  0.000650439  0.000579475  0.000496752  0.000409751  0.00032522   0.000248376  0.000182523  0.000129063  8.78141e-5   5.74912e-5   3.62172e-5   2.19535e-5   1.28047e-5   7.1864e-6    3.88087e-6   2.01662e-6   1.00831e-6   4.85109e-7   2.24575e-7   1.00037e-7   4.2878e-8    1.76842e-8
 -1.91905e-10   2.59911e-8    6.30193e-8    1.47028e-7    3.30066e-7    7.12982e-7    1.48195e-6    2.96389e-6    5.70385e-6    1.05621e-5    1.88195e-5    3.22659e-5    5.32297e-5    8.44968e-5    0.000129063   0.000189689   0.000268261   0.000365047   0.000477986   0.000602225   0.000730093   0.000851675   0.000955973   0.00103251    0.00107304   0.00107304   0.00103251   0.000955973  0.000851675  0.000730093  0.000602225  0.000477986  0.000365047  0.000268261  0.000189689  0.000129063  8.44968e-5   5.32297e-5   3.22659e-5   1.88195e-5   1.05621e-5   5.70385e-6   2.96389e-6   1.48195e-6   7.12982e-7   3.30066e-7   1.47028e-7   6.30193e-8   2.59911e-8
 -1.71705e-10   3.67569e-8    8.91227e-8    2.07928e-7    4.66784e-7    1.00831e-6    2.09579e-6    4.19157e-6    8.06647e-6    1.49371e-5    2.66148e-5    4.56308e-5    7.52781e-5    0.000119497   0.000182523   0.000268261   0.000379378   0.000516254   0.000675975   0.000851675   0.00103251    0.00120445    0.00135195    0.00146019    0.00151751   0.00151751   0.00146019   0.00135195   0.00120445   0.00103251   0.000851675  0.000675975  0.000516254  0.000379378  0.000268261  0.000182523  0.000119497  7.52781e-5   4.56308e-5   2.66148e-5   1.49371e-5   8.06647e-6   4.19157e-6   2.09579e-6   1.00831e-6   4.66784e-7   2.07928e-7   8.91227e-8   3.67569e-8
 -1.51504e-10   5.00184e-8    1.21277e-7    2.82947e-7    6.35194e-7    1.3721e-6     2.85193e-6    5.70385e-6    1.09768e-5    2.03262e-5    3.62172e-5    6.2094e-5     0.000102438   0.00016261    0.000248376   0.000365047   0.000516254   0.000702513   0.00091986    0.00115895    0.00140503    0.001639      0.00183972    0.00198701    0.00206502   0.00206502   0.00198701   0.00183972   0.001639     0.00140503   0.00115895   0.00091986   0.000702513  0.000516254  0.000365047  0.000248376  0.00016261   0.000102438  6.2094e-5    3.62172e-5   2.03262e-5   1.09768e-5   5.70385e-6   2.85193e-6   1.3721e-6    6.35194e-7   2.82947e-7   1.21277e-7   5.00184e-8
 -1.31304e-10   6.54933e-8    1.58799e-7    3.70486e-7    8.31714e-7    1.7966e-6     3.73427e-6    7.46854e-6    1.43728e-5    2.66148e-5    4.74222e-5    8.13049e-5    0.00013413    0.000212919   0.00032522    0.000477986   0.000675975   0.00091986    0.00120445    0.00151751    0.00183972    0.00214609    0.0024089     0.00260176    0.0027039    0.0027039    0.00260176   0.0024089    0.00214609   0.00183972   0.00151751   0.00120445   0.00091986   0.000675975  0.000477986  0.00032522   0.000212919  0.00013413   8.13049e-5   4.74222e-5   2.66148e-5   1.43728e-5   7.46854e-6   3.73427e-6   1.7966e-6    8.31714e-7   3.70486e-7   1.58799e-7   6.54933e-8
 -1.11103e-10   8.25164e-8    2.00074e-7    4.66784e-7    1.04789e-6    2.26358e-6    4.70488e-6    9.40977e-6    1.81086e-5    3.35326e-5    5.97483e-5    0.000102438   0.000168994   0.000268261   0.000409751   0.000602225   0.000851675   0.00115895    0.00151751    0.00191195    0.0023179     0.0027039     0.00303502    0.00327801    0.0034067    0.0034067    0.00327801   0.00303502   0.0027039    0.0023179    0.00191195   0.00151751   0.00115895   0.000851675  0.000602225  0.000409751  0.000268261  0.000168994  0.000102438  5.97483e-5   3.35326e-5   1.81086e-5   9.40977e-6   4.70488e-6   2.26358e-6   1.04789e-6   4.66784e-7   2.00074e-7   8.25164e-8
 -9.09026e-11   1.00037e-7    2.42555e-7    5.65894e-7    1.27039e-6    2.74419e-6    5.70385e-6    1.14077e-5    2.19535e-5    4.06524e-5    7.24344e-5    0.000124188   0.000204875   0.00032522    0.000496752   0.000730093   0.00103251    0.00140503    0.00183972    0.0023179     0.00281005    0.00327801    0.00367944    0.00397401    0.00413003   0.00413003   0.00397401   0.00367944   0.00327801   0.00281005   0.0023179    0.00183972   0.00140503   0.00103251   0.000730093  0.000496752  0.00032522   0.000204875  0.000124188  7.24344e-5   4.06524e-5   2.19535e-5   1.14077e-5   5.70385e-6   2.74419e-6   1.27039e-6   5.65894e-7   2.42555e-7   1.00037e-7
 -7.0702e-11    1.16696e-7    2.82947e-7    6.60132e-7    1.48195e-6    3.20118e-6    6.65371e-6    1.33074e-5    2.56094e-5    4.74222e-5    8.44968e-5    0.000144869   0.000238993   0.000379378   0.000579475   0.000851675   0.00120445    0.001639      0.00214609    0.0027039     0.00327801    0.00382389    0.00429217    0.0046358     0.0048178    0.0048178    0.0046358    0.00429217   0.00382389   0.00327801   0.0027039    0.00214609   0.001639     0.00120445   0.000851675  0.000579475  0.000379378  0.000238993  0.000144869  8.44968e-5   4.74222e-5   2.56094e-5   1.33074e-5   6.65371e-6   3.20118e-6   1.48195e-6   6.60132e-7   2.82947e-7   1.16696e-7
 -5.05014e-11   1.30987e-7    3.17597e-7    7.40973e-7    1.66343e-6    3.5932e-6     7.46854e-6    1.49371e-5    2.87456e-5    5.32297e-5    9.48445e-5    0.00016261    0.000268261   0.000425837   0.000650439   0.000955973   0.00135195    0.00183972    0.0024089     0.00303502    0.00367944    0.00429217    0.0048178     0.00520351    0.0054078    0.0054078    0.00520351   0.0048178    0.00429217   0.00367944   0.00303502   0.0024089    0.00183972   0.00135195   0.000955973  0.000650439  0.000425837  0.000268261  0.00016261   9.48445e-5   5.32297e-5   2.87456e-5   1.49371e-5   7.46854e-6   3.5932e-6    1.66343e-6   7.40973e-7   3.17597e-7   1.30987e-7
 -3.03009e-11   1.41473e-7    3.43024e-7    8.00295e-7    1.7966e-6     3.88087e-6    8.06647e-6    1.61329e-5    3.1047e-5     5.74912e-5    0.000102438   0.000175628   0.000289738   0.00045993    0.000702513   0.00103251    0.00146019    0.00198701    0.00260176    0.00327801    0.00397401    0.0046358     0.00520351    0.0056201     0.00584074   0.00584074   0.0056201    0.00520351   0.0046358    0.00397401   0.00327801   0.00260176   0.00198701   0.00146019   0.00103251   0.000702513  0.00045993   0.000289738  0.000175628  0.000102438  5.74912e-5   3.1047e-5    1.61329e-5   8.06647e-6   3.88087e-6   1.7966e-6    8.00295e-7   3.43024e-7   1.41473e-7
 -1.01003e-11   1.47028e-7    3.56491e-7    8.31714e-7    1.86713e-6    4.03323e-6    8.38315e-6    1.67663e-5    3.22659e-5    5.97483e-5    0.000106459   0.000182523   0.000301113   0.000477986   0.000730093   0.00107304    0.00151751    0.00206502    0.0027039     0.0034067     0.00413003    0.0048178     0.0054078     0.00584074    0.00607005   0.00607005   0.00584074   0.0054078    0.0048178    0.00413003   0.0034067    0.0027039    0.00206502   0.00151751   0.00107304   0.000730093  0.000477986  0.000301113  0.000182523  0.000106459  5.97483e-5   3.22659e-5   1.67663e-5   8.38315e-6   4.03323e-6   1.86713e-6   8.31714e-7   3.56491e-7   1.47028e-7
  1.01003e-11   1.47028e-7    3.56491e-7    8.31714e-7    1.86713e-6    4.03323e-6    8.38315e-6    1.67663e-5    3.22659e-5    5.97483e-5    0.000106459   0.000182523   0.000301113   0.000477986   0.000730093   0.00107304    0.00151751    0.00206502    0.0027039     0.0034067     0.00413003    0.0048178     0.0054078     0.00584074    0.00607005   0.00607005   0.00584074   0.0054078    0.0048178    0.00413003   0.0034067    0.0027039    0.00206502   0.00151751   0.00107304   0.000730093  0.000477986  0.000301113  0.000182523  0.000106459  5.97483e-5   3.22659e-5   1.67663e-5   8.38315e-6   4.03323e-6   1.86713e-6   8.31714e-7   3.56491e-7   1.47028e-7
  3.03009e-11   1.41473e-7    3.43024e-7    8.00295e-7    1.7966e-6     3.88087e-6    8.06647e-6    1.61329e-5    3.1047e-5     5.74912e-5    0.000102438   0.000175628   0.000289738   0.00045993    0.000702513   0.00103251    0.00146019    0.00198701    0.00260176    0.00327801    0.00397401    0.0046358     0.00520351    0.0056201     0.00584074   0.00584074   0.0056201    0.00520351   0.0046358    0.00397401   0.00327801   0.00260176   0.00198701   0.00146019   0.00103251   0.000702513  0.00045993   0.000289738  0.000175628  0.000102438  5.74912e-5   3.1047e-5    1.61329e-5   8.06647e-6   3.88087e-6   1.7966e-6    8.00295e-7   3.43024e-7   1.41473e-7
  5.05014e-11   1.30987e-7    3.17597e-7    7.40973e-7    1.66343e-6    3.5932e-6     7.46854e-6    1.49371e-5    2.87456e-5    5.32297e-5    9.48445e-5    0.00016261    0.000268261   0.000425837   0.000650439   0.000955973   0.00135195    0.00183972    0.0024089     0.00303502    0.00367944    0.00429217    0.0048178     0.00520351    0.0054078    0.0054078    0.00520351   0.0048178    0.00429217   0.00367944   0.00303502   0.0024089    0.00183972   0.00135195   0.000955973  0.000650439  0.000425837  0.000268261  0.00016261   9.48445e-5   5.32297e-5   2.87456e-5   1.49371e-5   7.46854e-6   3.5932e-6    1.66343e-6   7.40973e-7   3.17597e-7   1.30987e-7
  7.0702e-11    1.16696e-7    2.82947e-7    6.60132e-7    1.48195e-6    3.20118e-6    6.65371e-6    1.33074e-5    2.56094e-5    4.74222e-5    8.44968e-5    0.000144869   0.000238993   0.000379378   0.000579475   0.000851675   0.00120445    0.001639      0.00214609    0.0027039     0.00327801    0.00382389    0.00429217    0.0046358     0.0048178    0.0048178    0.0046358    0.00429217   0.00382389   0.00327801   0.0027039    0.00214609   0.001639     0.00120445   0.000851675  0.000579475  0.000379378  0.000238993  0.000144869  8.44968e-5   4.74222e-5   2.56094e-5   1.33074e-5   6.65371e-6   3.20118e-6   1.48195e-6   6.60132e-7   2.82947e-7   1.16696e-7
  9.09026e-11   1.00037e-7    2.42555e-7    5.65894e-7    1.27039e-6    2.74419e-6    5.70385e-6    1.14077e-5    2.19535e-5    4.06524e-5    7.24344e-5    0.000124188   0.000204875   0.00032522    0.000496752   0.000730093   0.00103251    0.00140503    0.00183972    0.0023179     0.00281005    0.00327801    0.00367944    0.00397401    0.00413003   0.00413003   0.00397401   0.00367944   0.00327801   0.00281005   0.0023179    0.00183972   0.00140503   0.00103251   0.000730093  0.000496752  0.00032522   0.000204875  0.000124188  7.24344e-5   4.06524e-5   2.19535e-5   1.14077e-5   5.70385e-6   2.74419e-6   1.27039e-6   5.65894e-7   2.42555e-7   1.00037e-7
  1.11103e-10   8.25164e-8    2.00074e-7    4.66784e-7    1.04789e-6    2.26358e-6    4.70488e-6    9.40977e-6    1.81086e-5    3.35326e-5    5.97483e-5    0.000102438   0.000168994   0.000268261   0.000409751   0.000602225   0.000851675   0.00115895    0.00151751    0.00191195    0.0023179     0.0027039     0.00303502    0.00327801    0.0034067    0.0034067    0.00327801   0.00303502   0.0027039    0.0023179    0.00191195   0.00151751   0.00115895   0.000851675  0.000602225  0.000409751  0.000268261  0.000168994  0.000102438  5.97483e-5   3.35326e-5   1.81086e-5   9.40977e-6   4.70488e-6   2.26358e-6   1.04789e-6   4.66784e-7   2.00074e-7   8.25164e-8
  1.31304e-10   6.54933e-8    1.58799e-7    3.70486e-7    8.31714e-7    1.7966e-6     3.73427e-6    7.46854e-6    1.43728e-5    2.66148e-5    4.74222e-5    8.13049e-5    0.00013413    0.000212919   0.00032522    0.000477986   0.000675975   0.00091986    0.00120445    0.00151751    0.00183972    0.00214609    0.0024089     0.00260176    0.0027039    0.0027039    0.00260176   0.0024089    0.00214609   0.00183972   0.00151751   0.00120445   0.00091986   0.000675975  0.000477986  0.00032522   0.000212919  0.00013413   8.13049e-5   4.74222e-5   2.66148e-5   1.43728e-5   7.46854e-6   3.73427e-6   1.7966e-6    8.31714e-7   3.70486e-7   1.58799e-7   6.54933e-8
  1.51504e-10   5.00184e-8    1.21277e-7    2.82947e-7    6.35194e-7    1.3721e-6     2.85193e-6    5.70385e-6    1.09768e-5    2.03262e-5    3.62172e-5    6.2094e-5     0.000102438   0.00016261    0.000248376   0.000365047   0.000516254   0.000702513   0.00091986    0.00115895    0.00140503    0.001639      0.00183972    0.00198701    0.00206502   0.00206502   0.00198701   0.00183972   0.001639     0.00140503   0.00115895   0.00091986   0.000702513  0.000516254  0.000365047  0.000248376  0.00016261   0.000102438  6.2094e-5    3.62172e-5   2.03262e-5   1.09768e-5   5.70385e-6   2.85193e-6   1.3721e-6    6.35194e-7   2.82947e-7   1.21277e-7   5.00184e-8
  1.71705e-10   3.67569e-8    8.91227e-8    2.07928e-7    4.66784e-7    1.00831e-6    2.09579e-6    4.19157e-6    8.06647e-6    1.49371e-5    2.66148e-5    4.56308e-5    7.52781e-5    0.000119497   0.000182523   0.000268261   0.000379378   0.000516254   0.000675975   0.000851675   0.00103251    0.00120445    0.00135195    0.00146019    0.00151751   0.00151751   0.00146019   0.00135195   0.00120445   0.00103251   0.000851675  0.000675975  0.000516254  0.000379378  0.000268261  0.000182523  0.000119497  7.52781e-5   4.56308e-5   2.66148e-5   1.49371e-5   8.06647e-6   4.19157e-6   2.09579e-6   1.00831e-6   4.66784e-7   2.07928e-7   8.91227e-8   3.67569e-8
  1.91905e-10   2.59911e-8    6.30193e-8    1.47028e-7    3.30066e-7    7.12982e-7    1.48195e-6    2.96389e-6    5.70385e-6    1.05621e-5    1.88195e-5    3.22659e-5    5.32297e-5    8.44968e-5    0.000129063   0.000189689   0.000268261   0.000365047   0.000477986   0.000602225   0.000730093   0.000851675   0.000955973   0.00103251    0.00107304   0.00107304   0.00103251   0.000955973  0.000851675  0.000730093  0.000602225  0.000477986  0.000365047  0.000268261  0.000189689  0.000129063  8.44968e-5   5.32297e-5   3.22659e-5   1.88195e-5   1.05621e-5   5.70385e-6   2.96389e-6   1.48195e-6   7.12982e-7   3.30066e-7   1.47028e-7   6.30193e-8   2.59911e-8
  2.12106e-10   1.76842e-8    4.2878e-8     1.00037e-7    2.24575e-7    4.85109e-7    1.00831e-6    2.01662e-6    3.88087e-6    7.1864e-6     1.28047e-5    2.19535e-5    3.62172e-5    5.74912e-5    8.78141e-5    0.000129063   0.000182523   0.000248376   0.00032522    0.000409751   0.000496752   0.000579475   0.000650439   0.000702513   0.000730093  0.000730093  0.000702513  0.000650439  0.000579475  0.000496752  0.000409751  0.00032522   0.000248376  0.000182523  0.000129063  8.78141e-5   5.74912e-5   3.62172e-5   2.19535e-5   1.28047e-5   7.1864e-6    3.88087e-6   2.01662e-6   1.00831e-6   4.85109e-7   2.24575e-7   1.00037e-7   4.2878e-8    1.76842e-8
  2.32307e-10   1.15777e-8    2.80719e-8    6.54933e-8    1.47028e-7    3.17597e-7    6.60132e-7    1.32026e-6    2.54078e-6    4.70488e-6    8.38315e-6    1.43728e-5    2.37111e-5    3.76391e-5    5.74912e-5    8.44968e-5    0.000119497   0.00016261    0.000212919   0.000268261   0.00032522    0.000379378   0.000425837   0.00045993    0.000477986  0.000477986  0.00045993   0.000425837  0.000379378  0.00032522   0.000268261  0.000212919  0.00016261   0.000119497  8.44968e-5   5.74912e-5   3.76391e-5   2.37111e-5   1.43728e-5   8.38315e-6   4.70488e-6   2.54078e-6   1.32026e-6   6.60132e-7   3.17597e-7   1.47028e-7   6.54933e-8   2.80719e-8   1.15777e-8
  2.52507e-10   7.29349e-9    1.76842e-8    4.12582e-8    9.26216e-8    2.00074e-7    4.15857e-7    8.31714e-7    1.60059e-6    2.96389e-6    5.28105e-6    9.0543e-6     1.49371e-5    2.37111e-5    3.62172e-5    5.32297e-5    7.52781e-5    0.000102438   0.00013413    0.000168994   0.000204875   0.000238993   0.000268261   0.000289738   0.000301113  0.000301113  0.000289738  0.000268261  0.000238993  0.000204875  0.000168994  0.00013413   0.000102438  7.52781e-5   5.32297e-5   3.62172e-5   2.37111e-5   1.49371e-5   9.0543e-6    5.28105e-6   2.96389e-6   1.60059e-6   8.31714e-7   4.15857e-7   2.00074e-7   9.26216e-8   4.12582e-8   1.76842e-8   7.29349e-9
  2.72708e-10   4.42105e-9    1.07195e-8    2.50092e-8    5.61438e-8    1.21277e-7    2.52077e-7    5.04154e-7    9.70218e-7    1.7966e-6     3.20118e-6    5.48838e-6    9.0543e-6     1.43728e-5    2.19535e-5    3.22659e-5    4.56308e-5    6.2094e-5     8.13049e-5    0.000102438   0.000124188   0.000144869   0.00016261    0.000175628   0.000182523  0.000182523  0.000175628  0.00016261   0.000144869  0.000124188  0.000102438  8.13049e-5   6.2094e-5    4.56308e-5   3.22659e-5   2.19535e-5   1.43728e-5   9.0543e-6    5.48838e-6   3.20118e-6   1.7966e-6    9.70218e-7   5.04154e-7   2.52077e-7   1.21277e-7   5.61438e-8   2.50092e-8   1.07195e-8   4.42105e-9
  2.92908e-10   2.57864e-9    6.2523e-9     1.4587e-8     3.27467e-8    7.07367e-8    1.47028e-7    2.94055e-7    5.65894e-7    1.04789e-6    1.86713e-6    3.20118e-6    5.28105e-6    8.38315e-6    1.28047e-5    1.88195e-5    2.66148e-5    3.62172e-5    4.74222e-5    5.97483e-5    7.24344e-5    8.44968e-5    9.48445e-5    0.000102438   0.000106459  0.000106459  0.000102438  9.48445e-5   8.44968e-5   7.24344e-5   5.97483e-5   4.74222e-5   3.62172e-5   2.66148e-5   1.88195e-5   1.28047e-5   8.38315e-6   5.28105e-6   3.20118e-6   1.86713e-6   1.04789e-6   5.65894e-7   2.94055e-7   1.47028e-7   7.07367e-8   3.27467e-8   1.4587e-8    6.2523e-9    2.57864e-9
  3.13109e-10   1.44721e-9    3.50899e-9    8.18667e-9    1.83784e-8    3.96996e-8    8.25164e-8    1.65033e-7    3.17597e-7    5.8811e-7     1.04789e-6    1.7966e-6     2.96389e-6    4.70488e-6    7.1864e-6     1.05621e-5    1.49371e-5    2.03262e-5    2.66148e-5    3.35326e-5    4.06524e-5    4.74222e-5    5.32297e-5    5.74912e-5    5.97483e-5   5.97483e-5   5.74912e-5   5.32297e-5   4.74222e-5   4.06524e-5   3.35326e-5   2.66148e-5   2.03262e-5   1.49371e-5   1.05621e-5   7.1864e-6    4.70488e-6   2.96389e-6   1.7966e-6    1.04789e-6   5.8811e-7    3.17597e-7   1.65033e-7   8.25164e-8   3.96996e-8   1.83784e-8   8.18667e-9   3.50899e-9   1.44721e-9
  3.33309e-10   7.81538e-10   1.89496e-9    4.42105e-9    9.92491e-9    2.1439e-8     4.45613e-8    8.91227e-8    1.71512e-7    3.17597e-7    5.65894e-7    9.70218e-7    1.60059e-6    2.54078e-6    3.88087e-6    5.70385e-6    8.06647e-6    1.09768e-5    1.43728e-5    1.81086e-5    2.19535e-5    2.56094e-5    2.87456e-5    3.1047e-5     3.22659e-5   3.22659e-5   3.1047e-5    2.87456e-5   2.56094e-5   2.19535e-5   1.81086e-5   1.43728e-5   1.09768e-5   8.06647e-6   5.70385e-6   3.88087e-6   2.54078e-6   1.60059e-6   9.70218e-7   5.65894e-7   3.17597e-7   1.71512e-7   8.91227e-8   4.45613e-8   2.1439e-8    9.92491e-9   4.42105e-9   1.89496e-9   7.81538e-10
  3.5351e-10    4.0611e-10    9.84676e-10   2.29731e-9    5.15728e-9    1.11403e-8    2.31554e-8    4.63108e-8    8.91227e-8    1.65033e-7    2.94055e-7    5.04154e-7    8.31714e-7    1.32026e-6    2.01662e-6    2.96389e-6    4.19157e-6    5.70385e-6    7.46854e-6    9.40977e-6    1.14077e-5    1.33074e-5    1.49371e-5    1.61329e-5    1.67663e-5   1.67663e-5   1.61329e-5   1.49371e-5   1.33074e-5   1.14077e-5   9.40977e-6   7.46854e-6   5.70385e-6   4.19157e-6   2.96389e-6   2.01662e-6   1.32026e-6   8.31714e-7   5.04154e-7   2.94055e-7   1.65033e-7   8.91227e-8   4.63108e-8   2.31554e-8   1.11403e-8   5.15728e-9   2.29731e-9   9.84676e-10  4.0611e-10
  3.73711e-10   2.03055e-10   4.92338e-10   1.14865e-9    2.57864e-9    5.57017e-9    1.15777e-8    2.31554e-8    4.45613e-8    8.25164e-8    1.47028e-7    2.52077e-7    4.15857e-7    6.60132e-7    1.00831e-6    1.48195e-6    2.09579e-6    2.85193e-6    3.73427e-6    4.70488e-6    5.70385e-6    6.65371e-6    7.46854e-6    8.06647e-6    8.38315e-6   8.38315e-6   8.06647e-6   7.46854e-6   6.65371e-6   5.70385e-6   4.70488e-6   3.73427e-6   2.85193e-6   2.09579e-6   1.48195e-6   1.00831e-6   6.60132e-7   4.15857e-7   2.52077e-7   1.47028e-7   8.25164e-8   4.45613e-8   2.31554e-8   1.15777e-8   5.57017e-9   2.57864e-9   1.14865e-9   4.92338e-10  2.03055e-10
  3.93911e-10   9.76922e-11   2.3687e-10    5.52631e-10   1.24061e-9    2.67987e-9    5.57017e-9    1.11403e-8    2.1439e-8     3.96996e-8    7.07367e-8    1.21277e-7    2.00074e-7    3.17597e-7    4.85109e-7    7.12982e-7    1.00831e-6    1.3721e-6     1.7966e-6     2.26358e-6    2.74419e-6    3.20118e-6    3.5932e-6     3.88087e-6    4.03323e-6   4.03323e-6   3.88087e-6   3.5932e-6    3.20118e-6   2.74419e-6   2.26358e-6   1.7966e-6    1.3721e-6    1.00831e-6   7.12982e-7   4.85109e-7   3.17597e-7   2.00074e-7   1.21277e-7   7.07367e-8   3.96996e-8   2.1439e-8    1.11403e-8   5.57017e-9   2.67987e-9   1.24061e-9   5.52631e-10  2.3687e-10   9.76922e-11
  4.14112e-10   0.0           1.09656e-10   2.55833e-10   5.74327e-10   1.24061e-9    2.57864e-9    5.15728e-9    9.92491e-9    1.83784e-8    3.27467e-8    5.61438e-8    9.26216e-8    1.47028e-7    2.24575e-7    3.30066e-7    4.66784e-7    6.35194e-7    8.31714e-7    1.04789e-6    1.27039e-6    1.48195e-6    1.66343e-6    1.7966e-6     1.86713e-6   1.86713e-6   1.7966e-6    1.66343e-6   1.48195e-6   1.27039e-6   1.04789e-6   8.31714e-7   6.35194e-7   4.66784e-7   3.30066e-7   2.24575e-7   1.47028e-7   9.26216e-8   5.61438e-8   3.27467e-8   1.83784e-8   9.92491e-9   5.15728e-9   2.57864e-9   1.24061e-9   5.74327e-10  2.55833e-10  1.09656e-10  0.0
  4.34312e-10   0.0           0.0           1.13961e-10   2.55833e-10   5.52631e-10   1.14865e-9    2.29731e-9    4.42105e-9    8.18667e-9    1.4587e-8     2.50092e-8    4.12582e-8    6.54933e-8    1.00037e-7    1.47028e-7    2.07928e-7    2.82947e-7    3.70486e-7    4.66784e-7    5.65894e-7    6.60132e-7    7.40973e-7    8.00295e-7    8.31714e-7   8.31714e-7   8.00295e-7   7.40973e-7   6.60132e-7   5.65894e-7   4.66784e-7   3.70486e-7   2.82947e-7   2.07928e-7   1.47028e-7   1.00037e-7   6.54933e-8   4.12582e-8   2.50092e-8   1.4587e-8    8.18667e-9   4.42105e-9   2.29731e-9   1.14865e-9   5.52631e-10  2.55833e-10  1.13961e-10  0.0          0.0
  4.54513e-10   0.0           0.0           0.0           1.09656e-10   2.3687e-10    4.92338e-10   9.84676e-10   1.89496e-9    3.50899e-9    6.2523e-9     1.07195e-8    1.76842e-8    2.80719e-8    4.2878e-8     6.30193e-8    8.91227e-8    1.21277e-7    1.58799e-7    2.00074e-7    2.42555e-7    2.82947e-7    3.17597e-7    3.43024e-7    3.56491e-7   3.56491e-7   3.43024e-7   3.17597e-7   2.82947e-7   2.42555e-7   2.00074e-7   1.58799e-7   1.21277e-7   8.91227e-8   6.30193e-8   4.2878e-8    2.80719e-8   1.76842e-8   1.07195e-8   6.2523e-9    3.50899e-9   1.89496e-9   9.84676e-10  4.92338e-10  2.3687e-10   1.09656e-10  0.0          0.0          0.0
  4.74713e-10   0.0           0.0           0.0           0.0           9.76922e-11   2.03055e-10   4.0611e-10    7.81538e-10   1.44721e-9    2.57864e-9    4.42105e-9    7.29349e-9    1.15777e-8    1.76842e-8    2.59911e-8    3.67569e-8    5.00184e-8    6.54933e-8    8.25164e-8    1.00037e-7    1.16696e-7    1.30987e-7    1.41473e-7    1.47028e-7   1.47028e-7   1.41473e-7   1.30987e-7   1.16696e-7   1.00037e-7   8.25164e-8   6.54933e-8   5.00184e-8   3.67569e-8   2.59911e-8   1.76842e-8   1.15777e-8   7.29349e-9   4.42105e-9   2.57864e-9   1.44721e-9   7.81538e-10  4.0611e-10   2.03055e-10  9.76922e-11  0.0          0.0          0.0          0.0

For the image metadata we specify the grid and the total flux of the image, which is 1.0. Note that we specify the total flux out front since it is degenerate with an overall shift in the gain amplitudes.

julia

skymeta = (; mimg = mimg ./ flux(mimg), ftot = 0.6);

We use again use a GMRF prior similar to the Imaging a Black Hole using only Closure Quantities tutorial for the log-ratio transformed image. We use the same correlated image prior for the inverse-logit transformed total polarization. The mean total polarization fraction p0 is centered at -2.0 with a standard deviation of 2.0 which logit transformed puts most of the prior mass < 0.8 fractional polarization. The standard deviation of the total polarization fraction pσ again uses a Half-normal process. The angular parameters of the polarizaton are given by a uniform prior on the sphere.

julia

cprior = corr_image_prior(grid, dvis; order = 2)
skyprior = (
    σs = ntuple(Returns(truncated(Normal(0.0, 0.5); lower = 0.0)), 4),
    as = ntuple(Returns(cprior), 4),
)

skym = SkyModel(sky, skyprior, grid; metadata = skymeta)

SkyModel
  with map: sky
   on grid: 
RectiGrid(
executor: ComradeBase.Serial()
Dimensions: 
(↓ X Sampled{Float64} LinRange{Float64}(-4.747133960864206e-10, 4.747133960864206e-10, 48) ForwardOrdered Regular Points,
→ Y Sampled{Float64} LinRange{Float64}(-4.747133960864206e-10, 4.747133960864206e-10, 48) ForwardOrdered Regular Points)
)
   )

Now we build the instrument model. Due to the complexity of VLBI the instrument model is critical to the success of imaging and getting reliable results. For this example we will use the standard instrument model used in polarized EHT analyses expressed in the RIME formalism. Our Jones decomposition will be given by GDR, where G are the complex gains, D are the d-terms, and R is what we call the ideal instrument response, which is how an ideal interferometer using the feed basis we observe relative to some reference basis.

Given the possible flexibility in different parameterizations of the individual Jones matrices each Jones matrix requires the user to specify a function that converts from parameters to specific parameterization f the jones matrices.

For the complex gain matrix, we used the JonesG jones matrix. The first argument is now a function that converts from the parameters to the complex gain matrix. In this case, we will use a amplitude and phase decomposition of the complex gain matrix. Note that since the gain matrix is a diagonal 2x2 matrix the function must return a 2-element tuple. The first element of the tuple is the gain for the first polarization feed (R) and the second is the gain for the second polarization feed (L).

julia

function fgain(x)
    gR = exp(x.lgR + 1im * x.gpR)
    gL = gR * exp(x.lgrat + 1im * x.gprat)
    return gR, gL
end
G = JonesG(fgain)

Comrade.JonesG{typeof(Main.var"##225".fgain)}(Main.var"##225".fgain)

Similarly we provide a JonesD function for the leakage terms. Since we assume that we are in the small leakage limit, we will use the decomposition 1 d1 d2 1 Therefore, there are 2 free parameters for the JonesD our parameterization function must return a 2-element tuple. For d-terms we will use a re-im parameterization.

julia

function fdterms(x)
    dR = complex(x.dRx, x.dRy)
    dL = complex(x.dLx, x.dLy)
    return dR, dL
end
D = JonesD(fdterms)

Comrade.JonesD{typeof(Main.var"##225".fdterms)}(Main.var"##225".fdterms)

Finally we define our response Jones matrix. This matrix is a basis transform matrix plus the feed rotation angle for each station. These are typically set by the telescope so there are no free parameters, so no parameterization is necessary.

julia

R = JonesR(; add_fr = true)

Comrade.JonesR{Nothing}(nothing, true)

Finally, we build our total Jones matrix by using the JonesSandwich function. The first argument is a function that specifies how to combine each Jones matrix. In this case we will use the standard decomposition J = adjoint(R)_G_D*R, where we need to apply the adjoint of the feed rotaion matrix R because the data has feed rotation calibration.

julia

js(g, d, r) = adjoint(r) * g * d * r
J = JonesSandwich(js, G, D, R)

Comrade.JonesSandwich{Base.Splat{typeof(Main.var"##225".js)}, Tuple{Comrade.JonesG{typeof(Main.var"##225".fgain)}, Comrade.JonesD{typeof(Main.var"##225".fdterms)}, Comrade.JonesR{Nothing}}}(splat(js), (Comrade.JonesG{typeof(Main.var"##225".fgain)}(Main.var"##225".fgain), Comrade.JonesD{typeof(Main.var"##225".fdterms)}(Main.var"##225".fdterms), Comrade.JonesR{Nothing}(nothing, true)))

Note

This is a general note that for arrays with non-zero leakage, feed rotation calibration does not remove the impact of feed rotations on the instrument model. That is, when modeling feed rotation must be taken into account. This is because the R and D matrices are not commutative. Therefore, to recover the correct instrumental terms we must include the feed rotation calibration in the instrument model. This is not ideal when doing polarized modeling, especially for interferometers using a mixture of linear and circular feeds. For linear feeds R does not commute with G or D and applying feed rotation calibration before solving for gains can mix gains and leakage with feed rotation calibration terms breaking many of the typical assumptions about the stabilty of different instrument effects.

For the instrument prior, we will use a simple IID prior for the complex gains and d-terms. The IIDSitePrior function specifies that each site has the same prior and each value is independent on some time segment. The current time segments are

ScanSeg() which specifies each scan has an independent value
TrackSeg() which says that the value is constant over the track.
IntegSeg() which says that the value changes each integration time

For the released EHT data, the calibration procedure makes gains stable over each scan so we use ScanSeg for those quantities. The d-terms are typically stable over the track so we use TrackSeg for those.

julia

intprior = (
    lgR = ArrayPrior(IIDSitePrior(ScanSeg(), Normal(0.0, 0.2)); LM = IIDSitePrior(ScanSeg(), Normal(0.0, 1.0))),
    lgrat = ArrayPrior(IIDSitePrior(ScanSeg(), Normal(0.0, 0.1))),
    gpR = ArrayPrior(IIDSitePrior(ScanSeg(), DiagonalVonMises(0.0, inv(π^2))); refant = SEFDReference(0.0), phase = true),
    gprat = ArrayPrior(IIDSitePrior(ScanSeg(), DiagonalVonMises(0.0, inv(0.1^2))); refant = SingleReference(:AA, 0.0), phase = true),
    dRx = ArrayPrior(IIDSitePrior(TrackSeg(), Normal(0.0, 0.2))),
    dRy = ArrayPrior(IIDSitePrior(TrackSeg(), Normal(0.0, 0.2))),
    dLx = ArrayPrior(IIDSitePrior(TrackSeg(), Normal(0.0, 0.2))),
    dLy = ArrayPrior(IIDSitePrior(TrackSeg(), Normal(0.0, 0.2))),
)

(lgR = Comrade.ArrayPrior{Comrade.IIDSitePrior{Comrade.ScanSeg, Distributions.Normal{Float64}}, Base.Pairs{Symbol, Comrade.IIDSitePrior{Comrade.ScanSeg, Distributions.Normal{Float64}}, Tuple{Symbol}, @NamedTuple{LM::Comrade.IIDSitePrior{Comrade.ScanSeg, Distributions.Normal{Float64}}}}, Comrade.NoReference, Nothing}(Comrade.IIDSitePrior{Comrade.ScanSeg, Distributions.Normal{Float64}}(Comrade.ScanSeg(), Distributions.Normal{Float64}(μ=0.0, σ=0.2)), Base.Pairs{Symbol, Comrade.IIDSitePrior{Comrade.ScanSeg, Distributions.Normal{Float64}}, Tuple{Symbol}, @NamedTuple{LM::Comrade.IIDSitePrior{Comrade.ScanSeg, Distributions.Normal{Float64}}}}(:LM => Comrade.IIDSitePrior{Comrade.ScanSeg, Distributions.Normal{Float64}}(Comrade.ScanSeg(), Distributions.Normal{Float64}(μ=0.0, σ=1.0))), Comrade.NoReference(), false, nothing), lgrat = Comrade.ArrayPrior{Comrade.IIDSitePrior{Comrade.ScanSeg, Distributions.Normal{Float64}}, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}, Comrade.NoReference, Nothing}(Comrade.IIDSitePrior{Comrade.ScanSeg, Distributions.Normal{Float64}}(Comrade.ScanSeg(), Distributions.Normal{Float64}(μ=0.0, σ=0.1)), Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}(), Comrade.NoReference(), false, nothing), gpR = Comrade.ArrayPrior{Comrade.IIDSitePrior{Comrade.ScanSeg, VLBIImagePriors.DiagonalVonMises{Float64, Float64, Float64}}, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}, Comrade.SEFDReference{Float64}, Nothing}(Comrade.IIDSitePrior{Comrade.ScanSeg, VLBIImagePriors.DiagonalVonMises{Float64, Float64, Float64}}(Comrade.ScanSeg(), VLBIImagePriors.DiagonalVonMises{Float64, Float64, Float64}(μ=0.0, κ=0.10132118364233778, lnorm=-1.739120733481688)), Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}(), Comrade.SEFDReference{Float64}(0.0, 0), true, nothing), gprat = Comrade.ArrayPrior{Comrade.IIDSitePrior{Comrade.ScanSeg, VLBIImagePriors.DiagonalVonMises{Float64, Float64, Float64}}, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}, Comrade.SingleReference{Float64}, Nothing}(Comrade.IIDSitePrior{Comrade.ScanSeg, VLBIImagePriors.DiagonalVonMises{Float64, Float64, Float64}}(Comrade.ScanSeg(), VLBIImagePriors.DiagonalVonMises{Float64, Float64, Float64}(μ=0.0, κ=99.99999999999999, lnorm=1.3823902436480708)), Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}(), Comrade.SingleReference{Float64}(:AA, 0.0), true, nothing), dRx = Comrade.ArrayPrior{Comrade.IIDSitePrior{Comrade.TrackSeg, Distributions.Normal{Float64}}, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}, Comrade.NoReference, Nothing}(Comrade.IIDSitePrior{Comrade.TrackSeg, Distributions.Normal{Float64}}(Comrade.TrackSeg(), Distributions.Normal{Float64}(μ=0.0, σ=0.2)), Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}(), Comrade.NoReference(), false, nothing), dRy = Comrade.ArrayPrior{Comrade.IIDSitePrior{Comrade.TrackSeg, Distributions.Normal{Float64}}, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}, Comrade.NoReference, Nothing}(Comrade.IIDSitePrior{Comrade.TrackSeg, Distributions.Normal{Float64}}(Comrade.TrackSeg(), Distributions.Normal{Float64}(μ=0.0, σ=0.2)), Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}(), Comrade.NoReference(), false, nothing), dLx = Comrade.ArrayPrior{Comrade.IIDSitePrior{Comrade.TrackSeg, Distributions.Normal{Float64}}, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}, Comrade.NoReference, Nothing}(Comrade.IIDSitePrior{Comrade.TrackSeg, Distributions.Normal{Float64}}(Comrade.TrackSeg(), Distributions.Normal{Float64}(μ=0.0, σ=0.2)), Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}(), Comrade.NoReference(), false, nothing), dLy = Comrade.ArrayPrior{Comrade.IIDSitePrior{Comrade.TrackSeg, Distributions.Normal{Float64}}, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}, Comrade.NoReference, Nothing}(Comrade.IIDSitePrior{Comrade.TrackSeg, Distributions.Normal{Float64}}(Comrade.TrackSeg(), Distributions.Normal{Float64}(μ=0.0, σ=0.2)), Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}(), Comrade.NoReference(), false, nothing))

Finally, we can build our instrument model which takes a model for the Jones matrix J and priors for each term in the Jones matrix.

julia

intmodel = InstrumentModel(J, intprior)

InstrumentModel
  with Jones: JonesSandwich
  with reference basis: PolarizedTypes.CirBasis()

intmodel = InstrumentModel(JonesR(;add_fr=true)) Putting it all together, we form our likelihood and posterior objects for optimization and sampling, and specifying to use Enzyme.Reverse with runtime activity for AD.

julia

using Enzyme
post = VLBIPosterior(skym, intmodel, dvis)

VLBIPosterior
ObservedSkyModel
  with map: sky
   on grid: 
FourierDualDomain(
Algorithm: VLBISkyModels.NFFTAlg{Float64, AbstractNFFTs.PrecomputeFlags, UInt32}(1, 1.0e-9, AbstractNFFTs.TENSOR, 0x00000000)
Image Domain: RectiGrid(
executor: ComradeBase.Serial()
Dimensions: 
(↓ X Sampled{Float64} LinRange{Float64}(-4.747133960864206e-10, 4.747133960864206e-10, 48) ForwardOrdered Regular Points,
→ Y Sampled{Float64} LinRange{Float64}(-4.747133960864206e-10, 4.747133960864206e-10, 48) ForwardOrdered Regular Points)
)
Visibility Domain: UnstructuredDomain(
executor: ComradeBase.Serial()
Dimensions: 
189-element StructArray(::Vector{Float64}, ::Vector{Float64}, ::Vector{Float64}, ::Vector{Float64}) with eltype @NamedTuple{U::Float64, V::Float64, Ti::Float64, Fr::Float64}:
 (U = -4.404687701333328e9, V = -4.521597269333328e9, Ti = 0.5833333432674408, Fr = 2.27070703125e11)
 (U = -4.427688319999995e9, V = -4.558917845333328e9, Ti = 0.7333333566784859, Fr = 2.27070703125e11)
 (U = -4.422283775999995e9, V = -4.545737898666661e9, Ti = 0.7333333566784859, Fr = 2.27070703125e11)
 (U = -4.443824298666661e9, V = -4.596403783111106e9, Ti = 0.8833333253860474, Fr = 2.27070703125e11)
 (U = -4.444612451555551e9, V = -4.594719701333328e9, Ti = 0.8833333253860474, Fr = 2.27070703125e11)
 (U = -4.452459235555551e9, V = -4.700912867555551e9, Ti = 1.300000011920929, Fr = 2.27070703125e11)
 (U = -4.453204522666661e9, V = -4.699246847999995e9, Ti = 1.300000011920929, Fr = 2.27070703125e11)
 (U = -4.442525923555551e9, V = -4.738497991111106e9, Ti = 1.4500000029802322, Fr = 2.27070703125e11)
 (U = -4.446617087999995e9, V = -4.727102591999995e9, Ti = 1.4500000029802322, Fr = 2.27070703125e11)
 (U = -4.373388259555551e9, V = -4.848290346666661e9, Ti = 1.8916667103767395, Fr = 2.27070703125e11)
 (U = -4.374057457777773e9, V = -4.846647935999995e9, Ti = 1.8916667103767395, Fr = 2.27070703125e11)
 (U = 1.854972024888887e9, V = -4.900536604444439e9, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = -4.33647849244444e9, V = -4.885093333333328e9, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = 1.8543247111111093e9, V = -4.898899640888884e9, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = -4.337125802666661e9, V = -4.883456426666661e9, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = -6.191450481777771e9, V = 1.544323338368054e7, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = -4.1988920319999957e9, V = -4.985362616888884e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 1.9771115377777758e9, V = -3.616703032888885e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 2.112877287111109e9, V = -4.853924366222218e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = -4.1994733297777734e9, V = -4.983740188444439e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 2.1122959964444423e9, V = -4.852301823999995e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 1.9765302328888867e9, V = -3.6150805831111073e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = -6.311769287111104e9, V = -1.3143835066666654e8, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = -1.3576575533333316e8, V = 1.2372212337777765e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = -6.176003569777771e9, V = -1.368659580444443e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 2.2020455187692285e9, V = -4.835182867692303e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = 2.023443446153844e9, V = -3.5993280459487143e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = 2.2014904845128183e9, V = -4.833565380923072e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = 2.0228883987692285e9, V = -3.5977105394871755e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = -1.7860208246153826e8, V = 1.2358548479999986e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = 2.439166364444442e9, V = -4.776837418666661e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = 2.1385755875555534e9, V = -3.547005681777774e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -3.9131562524444404e9, V = -5.122736583111106e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = 2.438692103111109e9, V = -4.775232839111106e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -3.913630471111107e9, V = -5.121131932444439e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = 2.1381013582222202e9, V = -3.545401116444441e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -6.352322559999993e9, V = -3.4589914133333296e8, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -3.005907564444441e8, V = 1.229831726222221e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -6.051731839999993e9, V = -1.575730865777776e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = 2.511586922666664e9, V = -4.755918350222218e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = 2.170796600888887e9, V = -3.528796735999996e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = 2.170351103999998e9, V = -3.5271960746666627e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = 2.5111413973333306e9, V = -4.754317681777773e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = -3.4079030488888854e8, V = 1.2271216071111097e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = -3.554185649777774e9, V = -5.242140615111105e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.691997553777775e9, V = -4.694789262222218e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.2425047537777753e9, V = -3.4769514666666627e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.2421424639999976e9, V = -3.4753602986666627e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = -3.5545479253333297e9, V = -5.24054941866666e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.6916352782222195e9, V = -4.693198023111106e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = -4.4949279733333284e8, V = 1.2178377671111097e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = -6.246183196444438e9, V = -5.47351347555555e8, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = -5.796690360888883e9, V = -1.7651891164444425e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.2622677727179465e9, V = -3.457387467487176e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = 2.7506836742564077e9, V = -4.671151025230764e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -3.442546884923073e9, V = -5.272523263999994e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -3.4428772102564063e9, V = -5.270935092512815e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = 2.2619374342564077e9, V = -3.455799302564099e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = 2.750353309538459e9, V = -4.66956284061538e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -6.193230559179481e9, V = -6.013722551794866e8, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -4.88415901538461e8, V = 1.2137635511794858e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -5.704814683897429e9, V = -1.8151358063589723e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = 5.063708287999995e9, V = -4.2083771519999957e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.298526215111109e9, V = -3.400051128888885e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -3.088728042666663e9, V = -5.354635448888883e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.8947912462222195e9, V = -4.600179484444439e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 5.063473251555551e9, V = -4.206796074666662e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.894556095999997e9, V = -4.598598385777773e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.298291107555553e9, V = -3.398470051555552e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -3.0889631217777743e9, V = -5.35305430755555e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.1689170879999976e9, V = 3.918022879999996e8, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -5.983519260444438e9, V = -7.544559466666658e8, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -5.962650044444438e8, V = 1.2001283235555544e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -2.7651820871111083e9, V = 8.08326024888888e8, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -8.152436351999991e9, V = -1.1462582471111097e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -5.38725424355555e9, V = -1.954584263111109e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 5.20314781866666e9, V = -4.164995278222218e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.303663210666664e9, V = -3.3806049066666627e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -2.959920895999997e9, V = -5.380193535999994e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.934449208888886e9, V = -4.575548401777773e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 5.202945521777772e9, V = -4.163416078222218e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -2.96012315733333e9, V = -5.378614286222217e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.9342469404444413e9, V = -4.573969180444439e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.3034609279999976e9, V = -3.379025671111108e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.2686985813333306e9, V = 4.105531208888885e8, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -5.894370119111105e9, V = -8.046451235555547e8, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -6.307860088888882e8, V = 1.1949434986666653e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -2.8994846222222195e9, V = 7.843903822222214e8, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -8.163068671999991e9, V = -1.2151982364444432e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -5.26358409955555e9, V = -1.9995886115555534e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 5.54752803555555e9, V = -4.038701703111107e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 2.299188743111109e9, V = -3.3265329137777743e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 3.020574414222219e9, V = -4.505591765333328e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -2.5786923022222195e9, V = -5.445258367999994e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 5.547500060444439e9, V = -4.0388189439999957e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 5.545354601411759e9, V = -4.037995941647054e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 2.299206753882351e9, V = -3.325316984470585e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 3.0200180856470556e9, V = -4.504489261176466e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -2.5814593882352915e9, V = -5.443281573647054e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 5.545326531764701e9, V = -4.0381131670588193e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 2.5269535999999976e9, V = 4.668900488888884e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -7.213856906666659e8, V = 1.179058869333332e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -5.59926673066666e9, V = -9.396666328888879e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 2.5269256533333306e9, V = 4.667728097777773e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -3.248339306666663e9, V = 7.121688159999993e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -8.126220359111103e9, V = -1.406556682666665e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -4.877881031111106e9, V = -2.1187254968888867e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 3.248311303111108e9, V = -7.122860568888881e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 8.126192398222214e9, V = 1.4064394311111097e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 5.658309684512815e9, V = -3.9900336836923037e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 5.658283887589737e9, V = -3.990151154871791e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 3.0433165062564073e9, V = -4.479256681025637e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 2.290543504410254e9, V = -3.3066006843076887e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -2.4295591712820487e9, V = -5.467004468512815e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 5.658234788102558e9, V = -3.9884589423589706e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 3.0432416295384583e9, V = -4.477681939692303e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 2.2904686145641003e9, V = -3.305025916717945e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 5.658209004307686e9, V = -3.9885764069743543e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -2.429634061128203e9, V = -5.465429700923072e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 2.614993171692305e9, V = 4.8922299733333284e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -7.527729985641018e8, V = 1.1726559999999988e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -5.472875690666661e9, V = -9.87747757948717e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 2.6149673616410227e9, V = 4.891055195897431e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -3.367766186666663e9, V = 6.834330141538454e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -8.087868875487172e9, V = -1.4769707651282036e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -4.720102662564097e9, V = -2.160403784205126e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 3.3677403569230733e9, V = -6.835504902564095e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 8.087843052307683e9, V = 1.47685327753846e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 6.037485539555549e9, V = -3.7629412693333297e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 2.206725866666664e9, V = -3.2192776817777743e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 3.0838075448888855e9, V = -4.360287900444439e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 6.037469781333326e9, V = -3.763059541333329e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 6.037566023111104e9, V = -3.761366407111107e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 3.083888028444441e9, V = -4.358713059555551e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 2.206806371555553e9, V = -3.217702819555552e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 6.037550279111104e9, V = -3.7614846791111073e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 2.9536779662222195e9, V = 5.973466417777772e8, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = -8.77081679999999e8, V = 1.141010222222221e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 2.953662200888886e9, V = 5.97228362666666e8, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = -3.830759658666662e9, V = 5.436635751111104e8, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 3.8307439288888845e9, V = -5.43781858666666e8, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 6.193776597333326e9, V = -3.584673976888885e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 6.193768718222216e9, V = -3.584792625777774e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 2.0963110399999979e9, V = -3.1565621119999967e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 3.04824456533333e9, V = -4.2709149368888845e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 6.193972479999993e9, V = -3.583095103999996e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 2.0965068515555534e9, V = -3.154983210666663e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 3.0484403768888855e9, V = -4.269336042666662e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 6.193964600888882e9, V = -3.5832137315555515e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 3.145532039111108e9, V = 6.862409528888881e8, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 3.145524195555552e9, V = 6.861223146666659e8, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = -9.519335111111101e8, V = 1.114352821333332e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = -4.0974655644444404e9, V = 4.2811187466666627e8, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 4.0974577137777734e9, V = -4.2823050222222173e8, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 6.234329756444438e9, V = -3.385946503111108e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 1.931031367111109e9, V = -3.0921642239999967e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 6.234330837333326e9, V = -3.3860652231111073e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 2.9449131591111083e9, V = -4.1750833208888845e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 6.234647921777771e9, V = -3.3843593599999967e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 6.234648903111104e9, V = -3.3844781297777743e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 1.931349447111109e9, V = -3.090577116444441e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 2.94523125333333e9, V = -4.1734962275555515e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 3.289416654222219e9, V = 7.89136849777777e8, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 3.2894176639999967e9, V = 7.890181191111102e8, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = -1.0138817973333323e9, V = 1.0829191111111097e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = -4.303298439111107e9, V = 2.937822586666663e8, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 4.30329948444444e9, V = -2.939009928888886e8, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 6.151253688888882e9, V = -3.205430023111108e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 1.7430493191111093e9, V = -3.038615523555552e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 2.7939210951111083e9, V = -4.091441422222218e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 6.151262791111104e9, V = -3.205548579555552e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 6.159540360533327e9, V = -3.2139407530666633e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 2.804326297599997e9, V = -4.0944362495999956e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 6.159549064533327e9, V = -3.214059332266663e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 1.7550084863999982e9, V = -3.039883980799997e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 3.35733262933333e9, V = 8.86011391999999e8, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = -1.0508717404444433e9, V = 1.0528258951111101e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 3.357341724444441e9, V = 8.858928017777768e8, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = -4.408204373333328e9, V = 1.6681450088888872e8, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 4.408213447111106e9, V = -1.6693308977777758e8, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 6.086775295999993e9, V = -3.1345589279999967e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 2.719461119999997e9, V = -4.0595089759999957e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 1.6591904159999983e9, V = -3.0189068799999967e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 6.086787583999993e9, V = -3.1346773919999967e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 3.367314207999996e9, V = 9.24950019999999e8, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = -1.0602706839999988e9, V = 1.0406020399999988e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 3.367326447999996e9, V = 9.248315599999989e8, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = -4.427584863999995e9, V = 1.1565201249999988e8, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 4.427597119999995e9, V = -1.1577047599999988e8, Ti = 7.438888907432556, Fr = 2.27070703125e11)
)
   )
ObservedInstrumentModel
  with Jones: JonesSandwich
  with reference basis: PolarizedTypes.CirBasis()Data Products: Comrade.EHTCoherencyDatum

Reconstructing the Image and Instrument Effects

To sample from this posterior, it is convenient to move from our constrained parameter space to an unconstrained one (i.e., the support of the transformed posterior is (-∞, ∞)). This transformation is done using the asflat function.

julia

tpost = asflat(post)

TransformedVLBIPosterior(
VLBIPosterior
ObservedSkyModel
  with map: sky
   on grid: 
FourierDualDomain(
Algorithm: VLBISkyModels.NFFTAlg{Float64, AbstractNFFTs.PrecomputeFlags, UInt32}(1, 1.0e-9, AbstractNFFTs.TENSOR, 0x00000000)
Image Domain: RectiGrid(
executor: ComradeBase.Serial()
Dimensions: 
(↓ X Sampled{Float64} LinRange{Float64}(-4.747133960864206e-10, 4.747133960864206e-10, 48) ForwardOrdered Regular Points,
→ Y Sampled{Float64} LinRange{Float64}(-4.747133960864206e-10, 4.747133960864206e-10, 48) ForwardOrdered Regular Points)
)
Visibility Domain: UnstructuredDomain(
executor: ComradeBase.Serial()
Dimensions: 
189-element StructArray(::Vector{Float64}, ::Vector{Float64}, ::Vector{Float64}, ::Vector{Float64}) with eltype @NamedTuple{U::Float64, V::Float64, Ti::Float64, Fr::Float64}:
 (U = -4.404687701333328e9, V = -4.521597269333328e9, Ti = 0.5833333432674408, Fr = 2.27070703125e11)
 (U = -4.427688319999995e9, V = -4.558917845333328e9, Ti = 0.7333333566784859, Fr = 2.27070703125e11)
 (U = -4.422283775999995e9, V = -4.545737898666661e9, Ti = 0.7333333566784859, Fr = 2.27070703125e11)
 (U = -4.443824298666661e9, V = -4.596403783111106e9, Ti = 0.8833333253860474, Fr = 2.27070703125e11)
 (U = -4.444612451555551e9, V = -4.594719701333328e9, Ti = 0.8833333253860474, Fr = 2.27070703125e11)
 (U = -4.452459235555551e9, V = -4.700912867555551e9, Ti = 1.300000011920929, Fr = 2.27070703125e11)
 (U = -4.453204522666661e9, V = -4.699246847999995e9, Ti = 1.300000011920929, Fr = 2.27070703125e11)
 (U = -4.442525923555551e9, V = -4.738497991111106e9, Ti = 1.4500000029802322, Fr = 2.27070703125e11)
 (U = -4.446617087999995e9, V = -4.727102591999995e9, Ti = 1.4500000029802322, Fr = 2.27070703125e11)
 (U = -4.373388259555551e9, V = -4.848290346666661e9, Ti = 1.8916667103767395, Fr = 2.27070703125e11)
 (U = -4.374057457777773e9, V = -4.846647935999995e9, Ti = 1.8916667103767395, Fr = 2.27070703125e11)
 (U = 1.854972024888887e9, V = -4.900536604444439e9, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = -4.33647849244444e9, V = -4.885093333333328e9, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = 1.8543247111111093e9, V = -4.898899640888884e9, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = -4.337125802666661e9, V = -4.883456426666661e9, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = -6.191450481777771e9, V = 1.544323338368054e7, Ti = 2.0416667461395264, Fr = 2.27070703125e11)
 (U = -4.1988920319999957e9, V = -4.985362616888884e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 1.9771115377777758e9, V = -3.616703032888885e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 2.112877287111109e9, V = -4.853924366222218e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = -4.1994733297777734e9, V = -4.983740188444439e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 2.1122959964444423e9, V = -4.852301823999995e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 1.9765302328888867e9, V = -3.6150805831111073e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = -6.311769287111104e9, V = -1.3143835066666654e8, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = -1.3576575533333316e8, V = 1.2372212337777765e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = -6.176003569777771e9, V = -1.368659580444443e9, Ti = 2.4583332538604736, Fr = 2.27070703125e11)
 (U = 2.2020455187692285e9, V = -4.835182867692303e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = 2.023443446153844e9, V = -3.5993280459487143e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = 2.2014904845128183e9, V = -4.833565380923072e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = 2.0228883987692285e9, V = -3.5977105394871755e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = -1.7860208246153826e8, V = 1.2358548479999986e9, Ti = 2.612500011920929, Fr = 2.27070703125e11)
 (U = 2.439166364444442e9, V = -4.776837418666661e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = 2.1385755875555534e9, V = -3.547005681777774e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -3.9131562524444404e9, V = -5.122736583111106e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = 2.438692103111109e9, V = -4.775232839111106e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -3.913630471111107e9, V = -5.121131932444439e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = 2.1381013582222202e9, V = -3.545401116444441e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -6.352322559999993e9, V = -3.4589914133333296e8, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -3.005907564444441e8, V = 1.229831726222221e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = -6.051731839999993e9, V = -1.575730865777776e9, Ti = 3.0583332180976868, Fr = 2.27070703125e11)
 (U = 2.511586922666664e9, V = -4.755918350222218e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = 2.170796600888887e9, V = -3.528796735999996e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = 2.170351103999998e9, V = -3.5271960746666627e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = 2.5111413973333306e9, V = -4.754317681777773e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = -3.4079030488888854e8, V = 1.2271216071111097e9, Ti = 3.208333432674408, Fr = 2.27070703125e11)
 (U = -3.554185649777774e9, V = -5.242140615111105e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.691997553777775e9, V = -4.694789262222218e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.2425047537777753e9, V = -3.4769514666666627e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.2421424639999976e9, V = -3.4753602986666627e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = -3.5545479253333297e9, V = -5.24054941866666e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.6916352782222195e9, V = -4.693198023111106e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = -4.4949279733333284e8, V = 1.2178377671111097e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = -6.246183196444438e9, V = -5.47351347555555e8, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = -5.796690360888883e9, V = -1.7651891164444425e9, Ti = 3.6249999403953552, Fr = 2.27070703125e11)
 (U = 2.2622677727179465e9, V = -3.457387467487176e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = 2.7506836742564077e9, V = -4.671151025230764e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -3.442546884923073e9, V = -5.272523263999994e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -3.4428772102564063e9, V = -5.270935092512815e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = 2.2619374342564077e9, V = -3.455799302564099e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = 2.750353309538459e9, V = -4.66956284061538e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -6.193230559179481e9, V = -6.013722551794866e8, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -4.88415901538461e8, V = 1.2137635511794858e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = -5.704814683897429e9, V = -1.8151358063589723e9, Ti = 3.7791666984558105, Fr = 2.27070703125e11)
 (U = 5.063708287999995e9, V = -4.2083771519999957e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.298526215111109e9, V = -3.400051128888885e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -3.088728042666663e9, V = -5.354635448888883e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.8947912462222195e9, V = -4.600179484444439e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 5.063473251555551e9, V = -4.206796074666662e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.894556095999997e9, V = -4.598598385777773e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.298291107555553e9, V = -3.398470051555552e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -3.0889631217777743e9, V = -5.35305430755555e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 2.1689170879999976e9, V = 3.918022879999996e8, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -5.983519260444438e9, V = -7.544559466666658e8, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -5.962650044444438e8, V = 1.2001283235555544e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -2.7651820871111083e9, V = 8.08326024888888e8, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -8.152436351999991e9, V = -1.1462582471111097e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = -5.38725424355555e9, V = -1.954584263111109e9, Ti = 4.225000083446503, Fr = 2.27070703125e11)
 (U = 5.20314781866666e9, V = -4.164995278222218e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.303663210666664e9, V = -3.3806049066666627e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -2.959920895999997e9, V = -5.380193535999994e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.934449208888886e9, V = -4.575548401777773e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 5.202945521777772e9, V = -4.163416078222218e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -2.96012315733333e9, V = -5.378614286222217e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.9342469404444413e9, V = -4.573969180444439e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.3034609279999976e9, V = -3.379025671111108e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 2.2686985813333306e9, V = 4.105531208888885e8, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -5.894370119111105e9, V = -8.046451235555547e8, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -6.307860088888882e8, V = 1.1949434986666653e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -2.8994846222222195e9, V = 7.843903822222214e8, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -8.163068671999991e9, V = -1.2151982364444432e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = -5.26358409955555e9, V = -1.9995886115555534e9, Ti = 4.374999940395355, Fr = 2.27070703125e11)
 (U = 5.54752803555555e9, V = -4.038701703111107e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 2.299188743111109e9, V = -3.3265329137777743e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 3.020574414222219e9, V = -4.505591765333328e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -2.5786923022222195e9, V = -5.445258367999994e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 5.547500060444439e9, V = -4.0388189439999957e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 5.545354601411759e9, V = -4.037995941647054e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 2.299206753882351e9, V = -3.325316984470585e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 3.0200180856470556e9, V = -4.504489261176466e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -2.5814593882352915e9, V = -5.443281573647054e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 5.545326531764701e9, V = -4.0381131670588193e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 2.5269535999999976e9, V = 4.668900488888884e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -7.213856906666659e8, V = 1.179058869333332e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -5.59926673066666e9, V = -9.396666328888879e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 2.5269256533333306e9, V = 4.667728097777773e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -3.248339306666663e9, V = 7.121688159999993e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -8.126220359111103e9, V = -1.406556682666665e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = -4.877881031111106e9, V = -2.1187254968888867e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 3.248311303111108e9, V = -7.122860568888881e8, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 8.126192398222214e9, V = 1.4064394311111097e9, Ti = 4.791666805744171, Fr = 2.27070703125e11)
 (U = 5.658309684512815e9, V = -3.9900336836923037e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 5.658283887589737e9, V = -3.990151154871791e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 3.0433165062564073e9, V = -4.479256681025637e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 2.290543504410254e9, V = -3.3066006843076887e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -2.4295591712820487e9, V = -5.467004468512815e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 5.658234788102558e9, V = -3.9884589423589706e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 3.0432416295384583e9, V = -4.477681939692303e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 2.2904686145641003e9, V = -3.305025916717945e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 5.658209004307686e9, V = -3.9885764069743543e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -2.429634061128203e9, V = -5.465429700923072e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 2.614993171692305e9, V = 4.8922299733333284e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -7.527729985641018e8, V = 1.1726559999999988e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -5.472875690666661e9, V = -9.87747757948717e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 2.6149673616410227e9, V = 4.891055195897431e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -3.367766186666663e9, V = 6.834330141538454e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -8.087868875487172e9, V = -1.4769707651282036e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = -4.720102662564097e9, V = -2.160403784205126e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 3.3677403569230733e9, V = -6.835504902564095e8, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 8.087843052307683e9, V = 1.47685327753846e9, Ti = 4.945833384990692, Fr = 2.27070703125e11)
 (U = 6.037485539555549e9, V = -3.7629412693333297e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 2.206725866666664e9, V = -3.2192776817777743e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 3.0838075448888855e9, V = -4.360287900444439e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 6.037469781333326e9, V = -3.763059541333329e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 6.037566023111104e9, V = -3.761366407111107e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 3.083888028444441e9, V = -4.358713059555551e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 2.206806371555553e9, V = -3.217702819555552e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 6.037550279111104e9, V = -3.7614846791111073e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 2.9536779662222195e9, V = 5.973466417777772e8, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = -8.77081679999999e8, V = 1.141010222222221e9, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 2.953662200888886e9, V = 5.97228362666666e8, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = -3.830759658666662e9, V = 5.436635751111104e8, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 3.8307439288888845e9, V = -5.43781858666666e8, Ti = 5.633333265781403, Fr = 2.27070703125e11)
 (U = 6.193776597333326e9, V = -3.584673976888885e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 6.193768718222216e9, V = -3.584792625777774e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 2.0963110399999979e9, V = -3.1565621119999967e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 3.04824456533333e9, V = -4.2709149368888845e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 6.193972479999993e9, V = -3.583095103999996e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 2.0965068515555534e9, V = -3.154983210666663e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 3.0484403768888855e9, V = -4.269336042666662e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 6.193964600888882e9, V = -3.5832137315555515e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 3.145532039111108e9, V = 6.862409528888881e8, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 3.145524195555552e9, V = 6.861223146666659e8, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = -9.519335111111101e8, V = 1.114352821333332e9, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = -4.0974655644444404e9, V = 4.2811187466666627e8, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 4.0974577137777734e9, V = -4.2823050222222173e8, Ti = 6.1499998569488525, Fr = 2.27070703125e11)
 (U = 6.234329756444438e9, V = -3.385946503111108e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 1.931031367111109e9, V = -3.0921642239999967e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 6.234330837333326e9, V = -3.3860652231111073e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 2.9449131591111083e9, V = -4.1750833208888845e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 6.234647921777771e9, V = -3.3843593599999967e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 6.234648903111104e9, V = -3.3844781297777743e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 1.931349447111109e9, V = -3.090577116444441e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 2.94523125333333e9, V = -4.1734962275555515e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 3.289416654222219e9, V = 7.89136849777777e8, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 3.2894176639999967e9, V = 7.890181191111102e8, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = -1.0138817973333323e9, V = 1.0829191111111097e9, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = -4.303298439111107e9, V = 2.937822586666663e8, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 4.30329948444444e9, V = -2.939009928888886e8, Ti = 6.716666579246521, Fr = 2.27070703125e11)
 (U = 6.151253688888882e9, V = -3.205430023111108e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 1.7430493191111093e9, V = -3.038615523555552e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 2.7939210951111083e9, V = -4.091441422222218e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 6.151262791111104e9, V = -3.205548579555552e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 6.159540360533327e9, V = -3.2139407530666633e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 2.804326297599997e9, V = -4.0944362495999956e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 6.159549064533327e9, V = -3.214059332266663e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 1.7550084863999982e9, V = -3.039883980799997e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 3.35733262933333e9, V = 8.86011391999999e8, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = -1.0508717404444433e9, V = 1.0528258951111101e9, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 3.357341724444441e9, V = 8.858928017777768e8, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = -4.408204373333328e9, V = 1.6681450088888872e8, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 4.408213447111106e9, V = -1.6693308977777758e8, Ti = 7.233333349227905, Fr = 2.27070703125e11)
 (U = 6.086775295999993e9, V = -3.1345589279999967e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 2.719461119999997e9, V = -4.0595089759999957e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 1.6591904159999983e9, V = -3.0189068799999967e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 6.086787583999993e9, V = -3.1346773919999967e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 3.367314207999996e9, V = 9.24950019999999e8, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = -1.0602706839999988e9, V = 1.0406020399999988e9, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 3.367326447999996e9, V = 9.248315599999989e8, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = -4.427584863999995e9, V = 1.1565201249999988e8, Ti = 7.438888907432556, Fr = 2.27070703125e11)
 (U = 4.427597119999995e9, V = -1.1577047599999988e8, Ti = 7.438888907432556, Fr = 2.27070703125e11)
)
   )
ObservedInstrumentModel
  with Jones: JonesSandwich
  with reference basis: PolarizedTypes.CirBasis()Data Products: Comrade.EHTCoherencyDatum
Transform: Params to ℝ^9788
)

We can also query the dimension of our posterior or the number of parameters we will sample.

Warning

This can often be different from what you would expect. This difference is especially true when using angular variables, where we often artificially increase the dimension of the parameter space to make sampling easier.

Now we optimize. Unlike other imaging examples, we move straight to gradient optimizers due to the higher dimension of the space. In addition the only AD package that can currently work with the polarized Comrade posterior is Enzyme.

julia

using Optimization, OptimizationLBFGSB
xopt, sol = comrade_opt(
    post, LBFGSB();
    initial_params = prior_sample(rng, post), maxiters = 2_000
)

((sky = (σs = (3.4883630420548557, 0.19395921725197157, 0.0827304065838507, 0.015938441793618956), as = ((params = [0.006965121540858039 0.014432824469917756 0.02150826470110013 0.028887192380432122 0.0391748299178757 0.05241183839609032 0.06592512433693179 0.07808189472391748 0.08793406043393062 0.09411159838821286 0.09442166406382835 0.08642357778209912 0.07157422458072914 0.05421540773269592 0.03769040156901786 0.02458147210110034 0.01668107337358237 0.015451294976972056 0.021135502645448646 0.031077176326085188 0.04160303213245424 0.048685439857156364 0.051384184241329595 0.05201050797292798 0.05439671864394901 0.06178271307288848 0.07418299920302764 0.08619198995802303 0.09094929912353515 0.08648584666859843 0.0760725992825777 0.06496687938370817 0.055957703401682296 0.047882690468777925 0.0394394917035164 0.032860995832359026 0.03272185180786724 0.04061341205271331 0.05319059692209448 0.06443858100329003 0.0714148507402758 0.07503990180724204 0.07529747571404045 0.07025776225784873 0.05820839068418109 0.04092504789760788 0.023828485810924824 0.010524026521625766; 0.01581694263135559 0.03103127199713078 0.04516256333213379 0.0594370231118243 0.07625965898006719 0.09680778178155575 0.12049738154131893 0.14479023487529175 0.16515097107014107 0.1756699089803913 0.17165750494551327 0.15513834378957825 0.13353643655196942 0.11181070633429177 0.09108841259191149 0.07219034360372507 0.05805894756724527 0.052729724819528326 0.05668078723923571 0.06744355780592293 0.08013273224785566 0.08898599769143997 0.09224829245427678 0.0922833255049301 0.09431028445748177 0.10277512389431821 0.1190844151294801 0.13666892673682252 0.14527525679060596 0.13990293092847317 0.12440317178848917 0.10647468401381525 0.09339670195803658 0.08577940366302488 0.07915991560375917 0.07210901693780082 0.06984393581044884 0.07834188159080338 0.09726869952238976 0.12096052209730078 0.14210772493593257 0.1538734093868815 0.15222449875266494 0.13762793476339713 0.11287996530649792 0.08177672993231665 0.050213405567694096 0.023074117435549636; 0.02390369821586987 0.044670327103820115 0.06360035689653584 0.0840697737851871 0.10816044563884812 0.13759274291230267 0.173257706152378 0.2110830863283754 0.24207018699706007 0.25623347598272184 0.25032958402906375 0.2329171051917569 0.21358834684303654 0.19408477793904694 0.17258475229872217 0.14894351229560618 0.12828772511256595 0.11491532174983726 0.1085639562700388 0.10830313619629302 0.11079468464315104 0.11276475727290168 0.11304980577217179 0.11408026522460907 0.11879089835106665 0.1293839090634548 0.14628236052062246 0.1650121282619636 0.17629801913727203 0.17301517240228892 0.15619594739909118 0.1332095946034372 0.11451081241355941 0.10608818678051533 0.10365674588928396 0.10169876286794738 0.10170540846806013 0.1110439336430747 0.13333288230916707 0.16543720185495006 0.199731083015544 0.22335767142802548 0.22467752006640782 0.20262832084584606 0.1648577655927122 0.11984704019757565 0.07475404437924231 0.03482741888735773; 0.027025297059447218 0.051118306426199474 0.07573126898350668 0.10511942672299304 0.14028701833874557 0.18264930482653965 0.2329347322826044 0.285387416899926 0.32827962775164615 0.35131847180086434 0.3540554395300044 0.34404234797891964 0.326848732779381 0.3043984815985692 0.2780766116643341 0.25088080402355367 0.2268733353048357 0.20581397745025165 0.18667138792702764 0.16911814618819576 0.1538078021005808 0.1419263938736237 0.13524821041808166 0.13845504703697725 0.15124548093544912 0.17054538801078614 0.19068860714104857 0.20655975976907837 0.21207612616361723 0.2034822635050828 0.1804732211458227 0.1493925166372989 0.12030634986967158 0.10351021377874015 0.09993726411625668 0.1047146272552462 0.11589124971849851 0.13502265408881506 0.16398683196493816 0.19976081851454747 0.2367042237773688 0.26614148647292785 0.27511974321779525 0.2554494556555845 0.21057833534146542 0.1521937581125785 0.09373449842872651 0.043365523576692516; 0.02823409862663277 0.058313391563027624 0.0934142478665728 0.1335959973038204 0.17828569634927668 0.2312932950918264 0.2946181588970854 0.3614874528478683 0.4191579614726725 0.4571500985921082 0.4725780659972054 0.4673655686583803 0.4470135466128601 0.420815562643215 0.39683747528060376 0.377388342381955 0.35702652173432087 0.33014083331235816 0.2971280685790435 0.2608618597468034 0.22721469871822791 0.20018266268518745 0.1850864978159918 0.18822243805749617 0.2097760549301807 0.24067340504558013 0.267893145280448 0.2789996264496017 0.2679179716456579 0.23817512967273996 0.19647111849678478 0.14966906166762994 0.10671192291962701 0.07793893813230206 0.06961371294257039 0.0792002916887578 0.10423119392297502 0.14047410863795237 0.1825422488991245 0.22473486874512857 0.2593556193038172 0.2821836073919334 0.28997913764433253 0.2750932410826109 0.23261424641925177 0.17042489700281135 0.10560612189347214 0.0492952002694859; 0.034258767397897946 0.07535010104436102 0.12265323613610032 0.1711637160905979 0.22205988380900565 0.28290545956098523 0.3568158708033918 0.4367526299794194 0.5081303087675313 0.5567950565579571 0.5757421060590628 0.567491126295934 0.5460978045454999 0.530401034869247 0.5298694802668792 0.5353981127383393 0.5270875298091783 0.4933398680692876 0.4372402768317044 0.3721737660652806 0.31188411679419037 0.2646998134554723 0.23749924308448606 0.23558054528511355 0.2608353799512184 0.30081854941393044 0.3372581025237761 0.3494275772777645 0.3256456902339769 0.2717185700400968 0.2056771276550829 0.13899637768112758 0.08054350078995283 0.0403100142080978 0.02706912064259459 0.03927139619855457 0.07199248392770607 0.12088997093299206 0.17637072970423964 0.22928268045053288 0.26773120818492535 0.2817816178338406 0.2754474306937536 0.2544995124448311 0.21587297376111256 0.16117396310567897 0.10267545062603754 0.04936157964539077; 0.04684133677805919 0.10087885732619885 0.1582316494378278 0.21370502999373245 0.2720637251029265 0.3423212562875388 0.42714283737650066 0.5173582288320604 0.5936802105243745 0.638324505975488 0.6462839284861978 0.6298826941275479 0.6156037940108118 0.6272729920917421 0.6679121437542117 0.7140380976248525 0.7305231504954688 0.6913009764812367 0.5976123252547011 0.4790807465873552 0.368066595177633 0.2845834041715552 0.23564366548482008 0.22313897630922713 0.24563751390001695 0.2899510623262152 0.33280136971011426 0.35072948759865236 0.32802978039946495 0.2673238296566445 0.18906093831752444 0.11042476144215145 0.04070583258328724 -0.00796201522698868 -0.023788750562203538 -0.006206826490019449 0.033832822336199234 0.08795814364210358 0.14715441311341743 0.20303396217897404 0.24655888476756804 0.2609977021906516 0.2424966989083158 0.20680310677822425 0.16507456977946014 0.11978788035000656 0.07586020775623288 0.03668670160170752; 0.06377856156779174 0.1302091704721758 0.1960179438198951 0.26093975742342257 0.33227417062269576 0.41699715192760106 0.513523547232455 0.6076767793837704 0.6768106176419159 0.7041770566594043 0.6923599686278118 0.6656744320934632 0.6583291303350978 0.6932652973531803 0.7702284802114966 0.8602389417261951 0.9096523279552732 0.8669146191863705 0.72646065188815 0.5356299376929623 0.3551747013414801 0.22357665463971385 0.14843224753677353 0.12467796633276158 0.14411481022984252 0.19132815177233906 0.23959842665128356 0.2639189523819364 0.24992079905226464 0.19997007857605595 0.1301245457849499 0.05590734475185427 -0.014260700690573239 -0.06791279167305093 -0.08867087853971006 -0.06809608474203273 -0.016938257283600915 0.0458718820487949 0.10509805693127663 0.1530579836139919 0.19016263559476138 0.20645811813201712 0.1877873477480315 0.14326319084378955 0.0948923457013221 0.054948921419788806 0.027124930738724205 0.010572014585912221; 0.08156690358406626 0.16121922536513494 0.23924823170249326 0.3207110654300206 0.41200305598933257 0.5142116265895446 0.6195843577225761 0.7113245688435471 0.7679389711069504 0.7764978832530562 0.7456178326697447 0.7044728581344312 0.6876475110321071 0.7201030996495993 0.8090234051854641 0.9254504476893625 0.9939741088380731 0.938906443908341 0.7546791767900465 0.5023295684913427 0.2633058903035922 0.0919206279423694 -0.004383962602173415 -0.0363124981707133 -0.016913925250876958 0.036264470239584186 0.0963514220433325 0.13539753295507148 0.13788636160890003 0.1058626690648912 0.0553179495286858 -0.001836876443175125 -0.06163513419957128 -0.11475382794468661 -0.1456330840502294 -0.13640728557616175 -0.08574631859736735 -0.016405714998278118 0.04476527071148565 0.08439221542781108 0.1080375774859962 0.11943682237059004 0.10631198147107714 0.06603751353433966 0.017682482339689637 -0.017859307807219886 -0.03064852182545963 -0.021613391512061406; 0.09825574425607536 0.19580885462492928 0.2956604761036165 0.40257343259856887 0.5186026233325053 0.638909208901221 0.7516340932312024 0.8405295936792196 0.8875666407735582 0.8823864061143042 0.8324731305960479 0.7651195628273203 0.7169062826569799 0.7213283749299543 0.7939131263392256 0.9018405361480513 0.9562045652905946 0.8777181399894228 0.6672739458541657 0.3884786310596397 0.12700022374793207 -0.060178012343678276 -0.16561866044265844 -0.20154393249439415 -0.18205509813356435 -0.12058504080763421 -0.04257937988197899 0.024031245650392812 0.05737704357101913 0.052698914928831955 0.02259624607742262 -0.018038838851305136 -0.06844754730446827 -0.12067756153139918 -0.16302123819882838 -0.17893313722572698 -0.15152452313072062 -0.09312387285975517 -0.03644849653669936 -0.004026475614951849 0.007546837178446885 0.012001941409362116 0.00560678518926598 -0.020904989091045167 -0.05813445348717686 -0.08427149124584613 -0.08260160221657906 -0.05061543355815171; 0.11733758072332266 0.23963230514748865 0.3701097891648245 0.5090317846165501 0.6526425294601634 0.7906357622406956 0.909711108144082 0.9973829252921148 1.0396520674305467 1.0241377695508087 0.9506634929051881 0.8443580092446337 0.7489143245836335 0.7077843248235899 0.739847132064647 0.8084990674005454 0.8286164195851144 0.7328124841367752 0.521333538617686 0.24935720260911892 -0.0068775462898381864 -0.19260991226792273 -0.29170989856073454 -0.3198647764768433 -0.29411013848519085 -0.22282988155633046 -0.12584003394073096 -0.02689208952505831 0.04760835870549021 0.08163211977416532 0.07499921791616031 0.04147890823548216 -0.014913128931069686 -0.08175068177077133 -0.13915987301862162 -0.18168495052481298 -0.19400072712119626 -0.16876633615225953 -0.12897383280976812 -0.10392911699300486 -0.10044371407870957 -0.10212680583362993 -0.10136258456370138 -0.10870835367415363 -0.12627659430518115 -0.13688674083851854 -0.12030580785343209 -0.07068210775648572; 0.14449663231692353 0.29769905133695057 0.46293421026954573 0.6353903053514257 0.8029964436697783 0.951021103005089 1.0699947780497545 1.1541175206807905 1.1935573572295592 1.1721816230732558 1.0782190851450382 0.9310593394194742 0.782038529687369 0.6847530265112564 0.6630918209177478 0.6877043884886244 0.6842939355641597 0.5907116554580428 0.40000379159596955 0.15145154099054614 -0.09541033316292274 -0.2795314163312707 -0.36682712652590227 -0.37420378282408706 -0.3286826165769965 -0.24365160330640676 -0.13172264662963268 -0.008136290964808475 0.10703450306428063 0.18646127739275573 0.20882983808687702 0.17316277891390397 0.09016004763683141 -0.017466754391993557 -0.10775500045320244 -0.17117018662703917 -0.21517895449131216 -0.2303179288342733 -0.21841101197926163 -0.2027189845251508 -0.20105724832931351 -0.2047208639617884 -0.1984669704562271 -0.18710688453119548 -0.1810676317926517 -0.172502636820561 -0.14204872349500483 -0.08113946632871226; 0.18014212716965497 0.3688737264422402 0.5680179155021103 0.7665775490767027 0.945290388740284 1.0897572172380756 1.197047304125172 1.2685947370759856 1.3021833619274719 1.281988918577435 1.1841173243857568 1.0147941511335357 0.8241343001838906 0.6719297939994351 0.5961895150009259 0.5874763116760863 0.5816654465056786 0.5089662242741404 0.34517499240499877 0.11778085638179528 -0.1187532640923688 -0.2966836258351205 -0.3715606455216919 -0.3577042341804591 -0.28675111928382635 -0.18552512441718597 -0.06760399777841362 0.058574942918491864 0.19040811015597123 0.3062414727054413 0.3618328324238314 0.3231965757903936 0.20285103631636733 0.04068973694018152 -0.10270378521053192 -0.19498258731287252 -0.2531590906714508 -0.2881538528341969 -0.29601808243493133 -0.28713974483648375 -0.2819773444214233 -0.28121797667710713 -0.26909833928519367 -0.24413772402817388 -0.21798831704481694 -0.19070723121312624 -0.1484418668498054 -0.08252027520603152; 0.2197614282568725 0.44384559184331107 0.6698995933539068 0.8823059883259995 1.0599049932827371 1.1916385572226322 1.2795510232565428 1.32994757274926 1.346547876008336 1.3201874693098534 1.230308691880194 1.0706950492588192 0.8699759541765014 0.6838344706576569 0.5659907941778837 0.528785409230195 0.5244144416466423 0.4734883399719531 0.33206156051940355 0.12644003948104046 -0.08787965421876824 -0.24750777236332405 -0.31155819210757757 -0.28764240578312356 -0.20006528717254524 -0.08710276123000842 0.03046306217677145 0.13764372394931962 0.24629715508086533 0.3568634227308657 0.42760056835680454 0.39144724213559684 0.24611258388378462 0.045210014805515064 -0.14204419652574238 -0.2672408903855634 -0.3362777747496205 -0.37046511560233053 -0.3751943279938487 -0.3577460897071783 -0.3383534700680166 -0.325968068972565 -0.3070171894395748 -0.27350486094606963 -0.23417612162015267 -0.19324803943009458 -0.14286057945678246 -0.07693561528047721; 0.2560893237156275 0.5106504326605328 0.7565357889289192 0.9760090001670512 1.1490439733466307 1.267772648637303 1.336423378219139 1.3595409524101578 1.3397121431960644 1.2817094729040996 1.1886667567584983 1.0554000461119504 0.8800268296086348 0.6935516678258904 0.5501744855372926 0.48251725445098675 0.4669807191599084 0.4282245959115313 0.3153604994177436 0.147124743975754 -0.0294311591346333 -0.1651367762984842 -0.22842019209224315 -0.21017068929380917 -0.12400108625301293 -0.006575526637234296 0.10473304482834164 0.17792178903079325 0.232623354911037 0.2883476458091534 0.3281236658290537 0.29017446438877903 0.15268930309009426 -0.04404712372420289 -0.23803801265218175 -0.3750419801247748 -0.44825330442017786 -0.47570778657125523 -0.46521016505228213 -0.42524843850103017 -0.3789274889235966 -0.3446966187502701 -0.31561142071215875 -0.2778168108562743 -0.23207849780731807 -0.18347968375951676 -0.12988773963317582 -0.06796921731391478; 0.2851210122048912 0.5651516050534273 0.8287426147171311 1.0556496241316882 1.2259090323641566 1.3335301802815285 1.3835827693966838 1.3770376136889038 1.3140346944629833 1.2126373523530556 1.0992079632060512 0.9794444529212181 0.8364247794882733 0.66789612363416 0.5098976919900002 0.4096898679799353 0.3707193380021158 0.33545084725340785 0.25527499641359175 0.13336491500942485 -0.002197026449277872 -0.11521416158323199 -0.17818980278461466 -0.17140755375706251 -0.09582689885044111 0.022412648865779525 0.11778234314141572 0.14556026536013705 0.13013074896635232 0.11200216909510653 0.09031614025016035 0.035087988007043866 -0.07526724632200851 -0.22752962172688965 -0.38507866482077274 -0.5002818814897283 -0.5585529412753935 -0.5733182820820745 -0.5492252372540583 -0.4884944871770026 -0.413358209633215 -0.35190506504937696 -0.30698363893481 -0.2640246352211216 -0.2167904906118187 -0.16725436391976556 -0.11533099482817741 -0.05928838807421922; 0.30920490835549314 0.6124297990442311 0.8955101657753658 1.1340693896443383 1.3043917619385703 1.3982900034199015 1.4218385653527696 1.3804911346572524 1.2796678744059062 1.1451900411114706 1.0123321905040221 0.8891749876588769 0.7546227856094307 0.593816534064271 0.4258320111617323 0.2984093128014248 0.23463803666380478 0.20007940527393994 0.1544409669950372 0.07744150620658918 -0.028646751151671535 -0.12884522903506251 -0.18634063649375013 -0.17161775425935172 -0.07917516931273948 0.045263365364481424 0.11845042753945728 0.09572257855046629 -0.0022228223513209786 -0.10185729792976392 -0.18731135468632315 -0.27186474505599706 -0.3641751743281558 -0.4672579256275421 -0.5695436921261108 -0.6363319113153392 -0.6552608743886238 -0.6416736134964369 -0.6007798678768532 -0.5278169073898679 -0.4355905186189831 -0.3533857511760049 -0.2929751661258701 -0.2431612258489367 -0.19525275101765477 -0.14914173219489604 -0.1032090962721869 -0.053593529554551815; 0.3341991202944086 0.6626866601863568 0.968773680529262 1.2223143911535375 1.3916974841186895 1.4608008324787327 1.4368521882325453 1.3422511614847898 1.2038897335013443 1.0554526736462662 0.9224790670040346 0.7977726669328132 0.6549007400364653 0.4820361647873613 0.29603213481902096 0.14661861175053617 0.07149254271861792 0.053084615936201576 0.05395239767195917 0.02722317845597929 -0.053669287164799934 -0.1481064535473218 -0.19457113688021074 -0.1451054958545283 -0.003866222607002805 0.14019007342813944 0.197316175867519 0.1360809026347283 -0.04694010099517897 -0.24786929540424635 -0.4055256868863167 -0.5283119369691552 -0.621154509908587 -0.6927104942679847 -0.7523616598770222 -0.7752572791202951 -0.7475061846617078 -0.6903313606400333 -0.6194194730815392 -0.5313977105815277 -0.430645813135756 -0.3395606677473937 -0.2710983607365754 -0.2177186039681662 -0.17157937624413216 -0.13138642520482757 -0.09307813177750493 -0.04969373383231921; 0.3635766629760484 0.7211941064183324 1.0527672077767292 1.3213985353623643 1.4852890649288706 1.51736038037577 1.4285423746144483 1.2650758511203268 1.0830829778357098 0.9292304023394846 0.8156075871702984 0.7083393238159583 0.5614769314411107 0.3624024072791845 0.1439962794471939 -0.029484948299154396 -0.11440576002189246 -0.11293724534965797 -0.0503092139128224 -0.0028554326413236008 -0.04316980796212087 -0.12029991321722536 -0.1431475587323422 -0.055933173768887304 0.13168502879277216 0.3086771770412408 0.37456061567976395 0.3023396156106483 0.06082185085673055 -0.2477982102619598 -0.4984817596851938 -0.6761720377354934 -0.7853805569779108 -0.8408861277284723 -0.8734312853772553 -0.8732006220903109 -0.8197899972651076 -0.7285465432896627 -0.6246326730321138 -0.5151781471390271 -0.4032866318256747 -0.3054762323654039 -0.233553424042788 -0.1814999257401465 -0.14167678876815484 -0.11108619801134878 -0.08248324278651774 -0.04592208988885551; 0.39424006796513394 0.7827957123689088 1.1411730932262731 1.4228909459401897 1.5722923689511383 1.5554500260993807 1.3998651149837913 1.175070095814568 0.9553802507349977 0.8010531273684225 0.7193356732522588 0.6487446126929014 0.5090853858299581 0.27835711027984295 0.015426785290587356 -0.1952691516818363 -0.30599906018709827 -0.29617606748055497 -0.17435378699519666 -0.04286881132187788 -0.012538701998766133 -0.04388235054032232 -0.03385272664608907 0.06381991364768662 0.24611958304872755 0.4256150200386239 0.5140881618293264 0.4626426476716007 0.21533762766051465 -0.14584723544402203 -0.46300194558589575 -0.6918829434652237 -0.8240596152710332 -0.8741367388824223 -0.8919942968328829 -0.88701287229241 -0.8348043133669738 -0.7372938947730997 -0.6193674973178911 -0.49571721935067653 -0.3724174295601917 -0.26463583092128273 -0.18533028267469678 -0.1332892687686249 -0.1023837535581219 -0.08524482808025477 -0.06904429162019328 -0.04090408770773173; 0.41898590995138196 0.8337240367453137 1.2147724948135834 1.5029445601999691 1.6275456324328308 1.5559749395286757 1.3424888906203525 1.0796656201346932 0.8491623957751863 0.7120157270147044 0.6691959878646015 0.6395722262644336 0.5129525067245928 0.251210974604628 -0.06333946807157319 -0.31995099085695217 -0.4584963556904392 -0.44504855091445866 -0.2847397394318616 -0.07803736085514515 0.05185976232412962 0.10024275446043777 0.12097146875394733 0.14929278752342015 0.2078997343442294 0.27414189064739797 0.3295958970440168 0.3411368366691661 0.18673240379951983 -0.09371948184778854 -0.37049442514073344 -0.5953097411086848 -0.7334242696894099 -0.7828165506173999 -0.7989500153471801 -0.8056166533031581 -0.7768667438940579 -0.6986662558225952 -0.5903932397813556 -0.47116478309192944 -0.34739725846362257 -0.23286856677626938 -0.14361686104219318 -0.08562741692790234 -0.05850989045047352 -0.05341981745116194 -0.05098065513438916 -0.03350167606467012; 0.42935194076352656 0.8569976155040284 1.2496574269501117 1.5356033326627596 1.631660016362128 1.5139270538790035 1.263379376775983 0.9910009133785191 0.7769861188875291 0.670202576829544 0.6647860879379449 0.6709108760102609 0.5556071678513829 0.2623119327482132 -0.10520811879716167 -0.40850056628491954 -0.5717020085712898 -0.5605261769546307 -0.37443102295304015 -0.08952089154162991 0.15046251615349263 0.28883895880638416 0.27360407518976315 0.15461025641865248 0.04028495135142799 -0.00742831674137122 0.02003441668944799 0.07361912178260005 0.03945580294875403 -0.09454375765643544 -0.26117706804974045 -0.42205814451917045 -0.5320639405871007 -0.5782379263354843 -0.6095120586767608 -0.6475192631695648 -0.6611200208982342 -0.6218902671288324 -0.5410042857485038 -0.4408096957507948 -0.32969914252470106 -0.21825983109553126 -0.12206487340288974 -0.054241779530520264 -0.023130308073780786 -0.022382471181028134 -0.02957388066446396 -0.02309045806683019; 0.4213944903026805 0.8425055544820889 1.2286517211354124 1.5045998526632962 1.5851065091308831 1.4519182847778522 1.1970230551870835 0.9395374293183174 0.7552343909686446 0.6774882841848034 0.6909820510773764 0.7074785513672621 0.5916799134985525 0.27525181241671065 -0.13482709292566306 -0.4815767523202871 -0.6663824101821665 -0.6547536362139378 -0.4466973055466813 -0.10106871866246524 0.2327360024035678 0.44036612196278674 0.34671521987662623 0.05930729048319607 -0.1756704483907843 -0.2787850083463834 -0.24472146930356495 -0.14018049282541992 -0.06871519837546464 -0.06946155133692 -0.12553448598279376 -0.209981464859601 -0.27384096712456674 -0.3090933690023397 -0.3609536207231597 -0.4396783211806941 -0.5076072409854283 -0.5243373685878061 -0.4868133713235043 -0.41577346000092796 -0.32424792117261353 -0.22311639745118958 -0.12616033258340326 -0.049187449389184984 -0.007944123203306439 -0.0023876057789390843 -0.011878620829104224 -0.013044630318917585; 0.3960398457084189 0.7930227693728252 1.1560674845379002 1.4160024425650806 1.4993400709950013 1.3895301655660812 1.1688207420224253 0.948565500081672 0.7955915641480574 0.7284373091162851 0.7241015731822977 0.705672837870781 0.5597524576553305 0.2295038324668612 -0.1966085515183373 -0.5629155906514381 -0.7492436813505468 -0.7232059134758252 -0.5025064166354396 -0.13276793481557553 0.2623193108912749 0.4898602751112333 0.3058847919125198 -0.08431490306542196 -0.3969459354987486 -0.5306192598757017 -0.48447046069425587 -0.3203865407135638 -0.1499831953361791 -0.03704068606144963 -0.0032748731723839875 -0.0262209019983451 -0.049968328248115576 -0.07616370936143085 -0.14354415373187057 -0.24794207909657381 -0.3520707987072561 -0.4181336168234153 -0.43156331314182284 -0.3994816864633805 -0.3334167531053162 -0.24687862067507452 -0.15343708060070146 -0.07032622653145171 -0.017608643180069307 -0.0006791318640572332 -0.004259299119607143 -0.006909541345178872; 0.3557689605285917 0.717880652284158 1.053622809486851 1.3011716936762354 1.40208165016838 1.34127818867364 1.1798802490017934 1.0089352501277347 0.881837456989239 0.8011811358823443 0.7397156632793873 0.644893154551765 0.4424874963361898 0.09848657605821982 -0.31953242082514205 -0.6723672759957704 -0.8410739339099125 -0.7951413196980298 -0.5618333616481884 -0.18993258635518137 0.2203408396290169 0.4503139241908563 0.23625019424862015 -0.18537260229377892 -0.5408072119338688 -0.6964573110468343 -0.6511256165807126 -0.46609303132118396 -0.2407655202448797 -0.04699796341251317 0.06716966413833064 0.10188681961665688 0.097103799157686 0.05741713303299034 -0.022237993490129022 -0.12533476908746355 -0.2344743694758084 -0.3277202122081954 -0.38218481142897803 -0.3886608276870031 -0.3516121470749606 -0.28377516359230776 -0.1982926932950459 -0.11234877559963642 -0.04782612460302697 -0.015580134760591401 -0.007573211284761714 -0.005973117468003795; 0.306771515004272 0.6283482724201102 0.940256223297298 1.1869731012626337 1.3169270453137463 1.3138680006532801 1.2185096902114927 1.0975518128365445 0.9864764694308417 0.875468441471155 0.7424305947546683 0.5688797052758718 0.3202753816377802 -0.02958673765516306 -0.43281067222805975 -0.7665278126786415 -0.9211747591544878 -0.8678856763844499 -0.6342376335768138 -0.27435380296133405 0.11776320645317814 0.36479101440901546 0.2094518430306457 -0.19210474355055698 -0.5463056168094161 -0.7108490259739404 -0.6920479930020444 -0.5401935925186853 -0.31830033058021306 -0.08543382785463097 0.09094558592493443 0.1701131081514503 0.16381461534432576 0.10338769833305071 0.02358097683975217 -0.06051005561786618 -0.15686560933539145 -0.25914258123435985 -0.34101026968703974 -0.38058594284535147 -0.37324695966531984 -0.3267400471893939 -0.25147737763397776 -0.16500202496425373 -0.09055264144517126 -0.042501317207833685 -0.019767122104407096 -0.009556132096210188; 0.25866767743908725 0.5390473996121528 0.8291550359962652 1.0803625043982248 1.2400383895434688 1.288803787688056 1.2544562529911545 1.1807292992925018 1.0803633959524879 0.9373976953858091 0.749129296212796 0.5277341293251318 0.2611350199045618 -0.07813027571109195 -0.4594198411204153 -0.7763750845954481 -0.928282900758375 -0.882668441965241 -0.6659087679512401 -0.33657696483761707 0.018591905832012954 0.2678542628398529 0.2170281716322968 -0.091126051473889 -0.40141738462670457 -0.5704773102738825 -0.5878179591530146 -0.48618242909872517 -0.30348659250792653 -0.08473914631355085 0.09822563117714012 0.18374368944346645 0.17342352603344122 0.11543558939746267 0.05087898829875857 -0.0144943406832697 -0.09985890098918776 -0.20559444323635268 -0.3040204337686708 -0.36886556912712093 -0.3894273822046187 -0.3646901466212181 -0.3011381581919347 -0.2171222122640477 -0.13619294197085038 -0.0750655225371515 -0.03832536052500799 -0.017316676659901165; 0.21455301784392336 0.4573702140966943 0.7276109938766113 0.9823327032291691 1.1636004468170644 1.2456779536569151 1.2505475801098076 1.2109060910184877 1.1235604980926444 0.9665732239722233 0.7550949780425726 0.5248127567852755 0.27108434779634744 -0.0426181726695816 -0.3955500589727299 -0.6878047042443284 -0.8274200554951837 -0.7837331371252331 -0.5835440136245947 -0.29870596348899187 -0.0067781741588478816 0.21266590831051324 0.25074831638103723 0.09094769064927166 -0.118105029967957 -0.25085062273036646 -0.28057762000331754 -0.22953834724798639 -0.1129943746571791 0.036304404570915334 0.15846040960995214 0.2016887507362382 0.1808753230640368 0.1375203030501147 0.09273296044579687 0.039304305872493325 -0.04526671412398119 -0.15713992908277383 -0.2677146391077079 -0.35275058908221274 -0.39686329458454034 -0.3904185787835418 -0.33700096350164954 -0.25689476831147084 -0.17414045655052715 -0.10545353796138988 -0.05795009518349285 -0.026395226899456167; 0.17057902411746548 0.3798225476120571 0.6338135130795304 0.8910920821343122 1.0872856546739214 1.185682598274862 1.2001874855091785 1.1638270830915562 1.0811721012468596 0.93510884864848 0.7405357854558563 0.5374260495875638 0.3230245417241148 0.05298197069111977 -0.2602910369238476 -0.5193822601612971 -0.6345564190062273 -0.5806476232991237 -0.3895969675657066 -0.1479641967525628 0.06281072818658659 0.2159341673367784 0.2857898579575852 0.26626971779066055 0.21068146086698414 0.17364708053724537 0.15365189465526669 0.1454183347003815 0.16915424400932128 0.21559686538383901 0.24142209582425322 0.22483726020413808 0.19247644958949578 0.16334676587981278 0.13671908706427524 0.090552149879886 0.0048421121587351405 -0.11067576759723971 -0.23159635361212247 -0.3349181011838987 -0.3973892936530589 -0.4020632264602672 -0.35434503606226814 -0.27842789636422 -0.19714720424868493 -0.12561777188592765 -0.07208916596594415 -0.03336946216040282; 0.12964599895067305 0.3069748350492629 0.542850602063195 0.7985364414434318 1.00656423095385 1.1152932417090058 1.122205072959333 1.062537941058248 0.9654716206300699 0.8351168866532092 0.6799024829984319 0.5241523199311479 0.36354896905732803 0.1546642586504798 -0.10323999070450283 -0.32615821280964047 -0.42226234130345386 -0.35987988485003763 -0.17631896074450384 0.02811530620765053 0.162766560341503 0.231624781319349 0.2760402172219539 0.31736030883430594 0.3755426730749698 0.4434613003357724 0.46477346410731624 0.41715978901245004 0.3423343687672981 0.2790821753255744 0.2249867559771903 0.18007136477124022 0.15720101664085503 0.15588023252329303 0.15606166783772493 0.12304549850227696 0.0413066340810278 -0.07718332084198957 -0.20876320815836058 -0.3241753259800826 -0.39199199932456824 -0.39657002805531394 -0.35041018866290835 -0.27903652037409593 -0.20236192788634338 -0.13341443446446732 -0.07921718688219066 -0.037217427193238166; 0.10054921336887998 0.24813699960129934 0.45776321053984675 0.7001991208638215 0.9135319135705966 1.034399948901627 1.0372694442315515 0.9497586483957055 0.8232505941805793 0.6917858695369198 0.565562125562579 0.4490121666099349 0.33194751764705915 0.17883906246815004 -0.019585346627395063 -0.20186092117287902 -0.2828182600562915 -0.22102250125301445 -0.05262143180793329 0.11867277086705731 0.2014172297539626 0.21143570001963194 0.21885932512653955 0.25350746206908337 0.3151745337963639 0.37527351817742755 0.38449394895081784 0.31653215275668445 0.20639902182716854 0.10786574354781063 0.040519820887250375 0.014786623687697625 0.03364486977382265 0.08049410288655114 0.1175343119275915 0.1058623981227445 0.03509206571008919 -0.08073604506794033 -0.21272388406302573 -0.3221596766783107 -0.3770997661858416 -0.3716990686696072 -0.32477859803128206 -0.25959276401017695 -0.19154761694012246 -0.13023378322994117 -0.080023006843108 -0.03833597617031121; 0.08509636501687327 0.2086025393041703 0.38770811166960517 0.6056339150138613 0.8130101961359727 0.9454751476570349 0.9594344419649771 0.8642356542255688 0.712481351460229 0.558623616189547 0.4294866608125911 0.3246689670154795 0.22382074179389114 0.09442597249109229 -0.06678397171652188 -0.2098673390133675 -0.27020444584443437 -0.21063678266384064 -0.0609900257247539 0.08470441996709555 0.14650740410535865 0.13761920614538617 0.12034910071980831 0.12303603992291377 0.13836390044161545 0.13871953591606448 0.09634558315345808 0.0007359464635001882 -0.1146811358281299 -0.2056951782785625 -0.24925650233128552 -0.23583466879494835 -0.17176237801103023 -0.08100040405027013 -0.007645729756680293 0.009823110570708284 -0.03832287745563277 -0.13561309178487227 -0.24478413922626413 -0.3243153252978953 -0.35119505217681 -0.33084703642674124 -0.28376642570371013 -0.22644290433598943 -0.16910904137078211 -0.11855527235372157 -0.07559638981147136 -0.03694428850826347; 0.08173534414862176 0.19054454387925693 0.3413165512001781 0.5277054092539666 0.7177715873404059 0.857850840128026 0.8968650094873926 0.8232197879543441 0.6724408424698193 0.4973269886998388 0.3390722372020565 0.21211060039711707 0.09856099952810118 -0.03663732094943436 -0.1942940118008222 -0.32150974612293154 -0.3689849364123777 -0.31894106085819446 -0.19163996291958074 -0.05832218279955758 0.01183393319626859 0.014094428887436814 -0.015073851669352796 -0.05509181164954624 -0.10504724778243585 -0.1708470394415909 -0.26000158179072225 -0.37475225239951077 -0.48751332854952156 -0.5601751375805686 -0.571919951742787 -0.5254236784620874 -0.4323836557878321 -0.3160392299572979 -0.21666836735630116 -0.1665872527137933 -0.1757155090219612 -0.2280657315050375 -0.2882157308517815 -0.32103948954661327 -0.3145490024613997 -0.2818571073834463 -0.23776866436293878 -0.18934157630184492 -0.14336905809203013 -0.10378477131619551 -0.0679679378075872 -0.0333589852198614; 0.09114475100715515 0.19590624996446698 0.32309349469687215 0.4736869794127061 0.6359779948122758 0.7765291280505762 0.8468741075864517 0.8170621688063714 0.6986594878002966 0.5287310119271604 0.34674417123166223 0.18134834664930008 0.03424299148240471 -0.12086212864403728 -0.2935375912048952 -0.4362355546798724 -0.4980970304675973 -0.47526601258732165 -0.38851894736169346 -0.28191376665686635 -0.20898441042096036 -0.19288214956700686 -0.22445430713083067 -0.2929987240459017 -0.39167445086935604 -0.5083575893676803 -0.6336744564526162 -0.7606896193956408 -0.8656010303455957 -0.9177976013554014 -0.905696502003329 -0.8399803316385603 -0.7307789125533642 -0.5990176258341481 -0.4758044257293005 -0.38638917200020584 -0.34061110701306235 -0.32885405512313043 -0.32483057017935496 -0.30460905233543756 -0.26935712078608365 -0.2319488005029934 -0.19463452906454437 -0.15635933720211706 -0.12107683519033553 -0.09002184434073622 -0.059771695628415514 -0.02934888503293671; 0.11361373417176773 0.2226800823275253 0.3301639936928437 0.44519532904481196 0.5749860204256584 0.7078950972768878 0.8045095604487398 0.8235258110098876 0.7556156872288744 0.6204938135738816 0.44589823549550694 0.2597700734453696 0.07903078665067488 -0.10259846668924011 -0.2952954656759652 -0.4690600027420218 -0.5720844002775551 -0.5931592028492857 -0.5553107370724025 -0.4927954693386755 -0.4468683145992632 -0.445913026125938 -0.49371242711441343 -0.5815988468340273 -0.7011596854810622 -0.8399819245886245 -0.9858065730159421 -1.1217433291612873 -1.2241711777180868 -1.2662342614021935 -1.2420534104321381 -1.1602695980864026 -1.0324725477391714 -0.8801997930133065 -0.7283113720166915 -0.5954940446851275 -0.4901946039420126 -0.4098391435884059 -0.34073316843110785 -0.2766700857435379 -0.22576648449220144 -0.189793095592401 -0.15983714418927458 -0.13098819127111425 -0.10440861530923583 -0.07914372833165592 -0.05263066262453199 -0.025697190663112487; 0.1436656792376954 0.26248858309657164 0.3550686838534696 0.440114726873128 0.5394772857490141 0.6580472533086138 0.7681456955287161 0.8259206759795731 0.8085196241091678 0.7220427463008504 0.5819120607746332 0.40680840740374424 0.21604767654721313 0.017150091517620362 -0.1913824859343886 -0.39233778879578934 -0.54372847252156 -0.6211481635808376 -0.6359642709091071 -0.6199744418957898 -0.6131247324540164 -0.6453013329607842 -0.724792176812919 -0.841412322612209 -0.9829323886852613 -1.1384141511169923 -1.29495350596717 -1.4322636898393626 -1.525746307404042 -1.5530293026762032 -1.5123961187062012 -1.4112038762411527 -1.265294422334882 -1.095111296871653 -0.9190775274692365 -0.7489280097153842 -0.593181111868346 -0.4561938988323119 -0.33982609187301427 -0.25138817090608395 -0.1951364671773387 -0.1618285096208894 -0.13797982744373766 -0.11703468889545775 -0.09606779745922125 -0.07217720848156585 -0.04617516026888773 -0.021784780282547617; 0.16842270135367454 0.2995480567257664 0.3871941539736309 0.45348116754255363 0.5274887427094087 0.6249810861925448 0.7322605984357442 0.8120433191594943 0.8347803066300303 0.7959407507711225 0.7014615801960304 0.5595311263559849 0.385579405756068 0.19339443751136595 -0.011791408251018938 -0.21949604015251895 -0.401212403619789 -0.5289565886055876 -0.5984971480053988 -0.6310138981607157 -0.66303321425524 -0.7246997963299658 -0.8289734623891699 -0.970884724563181 -1.1363390973255396 -1.3102616399812226 -1.4733370805392414 -1.6048670244828571 -1.6828519709397223 -1.6956429948515603 -1.6443330069058175 -1.536847640565984 -1.388427364996085 -1.2138799486080176 -1.0242608592211773 -0.828904915056222 -0.6397211443063401 -0.46899292443514734 -0.3307712554295513 -0.23621711134864348 -0.18216340089323352 -0.15238002872055728 -0.1327871462939792 -0.11610010078089412 -0.09556500929838806 -0.06861491563345376 -0.04099499396992274 -0.01839947936576653; 0.17600794844089637 0.3161983526897639 0.4108695636726765 0.47510848394960387 0.5331652113053649 0.6048586642697235 0.6930376166451467 0.7770696101726848 0.8269834002971226 0.8272490688373966 0.7770782177482078 0.6782497946550139 0.5397590640422564 0.3772823803584684 0.20103625176513132 0.017365316891699248 -0.1592516295652773 -0.30801886625556824 -0.4184881881923161 -0.4975319045629466 -0.5667732132999089 -0.6502125178309379 -0.7635829978211993 -0.9112878964470466 -1.0850327770158767 -1.2678944972447883 -1.4363454628300532 -1.5687974211394151 -1.647884640669006 -1.667138853654969 -1.6259872792733627 -1.5315949332352214 -1.3951436682918161 -1.2259111816710826 -1.0323936324385976 -0.8279689907100117 -0.6302599789490898 -0.4572062319992992 -0.3250467621409203 -0.23967654664405455 -0.1906960591044154 -0.16133976538793268 -0.14123557484074103 -0.12305995818540588 -0.09893515137064596 -0.06854172334594405 -0.03973923534485649 -0.017593339765569642; 0.1655043580213595 0.3065660377985985 0.41375850370078976 0.4909643805762027 0.5480541701663012 0.5985824575664327 0.6569407818557574 0.7255896876326964 0.7861726631342174 0.8157791134962354 0.805050769065936 0.7522294736660724 0.6603761544143759 0.5425739743848162 0.4121702396918492 0.2752598283835378 0.13645516827860116 0.004263377423339819 -0.11521446895343032 -0.22254766463994274 -0.3224698277186135 -0.42526054730352386 -0.5431744650618361 -0.685834260723179 -0.8536044235852898 -1.0337544146575028 -1.205210187907447 -1.3472816778963732 -1.4444706460211778 -1.4874260776449548 -1.4724752985874725 -1.4037562355800726 -1.288413201944469 -1.1344743351798314 -0.9542930272881325 -0.766863412492881 -0.5920647376512184 -0.44555556444059546 -0.33651043647787726 -0.2636216904581171 -0.21668879179487785 -0.18486218919445166 -0.16011422738721276 -0.13523997315574104 -0.10552528931283105 -0.07292935089197478 -0.04364514374016919 -0.020218835832658526; 0.14587544256938423 0.28040581337657455 0.39645583103655624 0.4905447016368727 0.5594876457879944 0.603961797089725 0.6370708419488456 0.6770792821744857 0.725871403160662 0.7675916752906167 0.7881268808780687 0.7807201026479919 0.7425202235594661 0.6802237181499439 0.6060934640973773 0.526931193778576 0.4435825955124973 0.35482313763802653 0.25812933655162984 0.15055524930704625 0.03396901468739044 -0.08862823711738728 -0.21917629735511046 -0.36338594112442807 -0.524673175028552 -0.6967957618765108 -0.8663507748640923 -1.01760093208902 -1.1358802997705446 -1.2087915158201783 -1.2296216199190142 -1.1968670316965482 -1.1138319328232984 -0.9907233327789989 -0.8447558659901633 -0.6956976106650087 -0.5599812233212491 -0.4475785463472235 -0.36143134942638677 -0.2985856315547413 -0.253687517994529 -0.21905536971960463 -0.18620238737038353 -0.15124035217991041 -0.11484425946775645 -0.07987182009149957 -0.04967059099157782 -0.02407044548838247; 0.12604942575933967 0.25055542276916226 0.3683911663088858 0.47290201456084285 0.5553260435409116 0.6073014008428659 0.6329282629743518 0.6509836174642516 0.6768108756628481 0.7101922753458557 0.7436271272823947 0.7694794452042429 0.7806591346245487 0.7766416833297433 0.7645146653703008 0.7496110894676463 0.7306696754112008 0.7001920394092065 0.6463324929301081 0.5596220744615665 0.44070468513472966 0.2999941023038902 0.14815748020869204 -0.010344405533343709 -0.17551129959374587 -0.3453992336508129 -0.5149507235993762 -0.6753703343383718 -0.814456416228998 -0.9196155680604917 -0.9810098588479097 -0.9904430301735216 -0.9476451200276671 -0.8647923098609099 -0.7603114108786028 -0.6505427090500426 -0.5480937355093888 -0.4610607712491113 -0.3913591425579014 -0.3367263824641819 -0.29329946244767485 -0.25340387124536906 -0.21039135818561364 -0.16553143255351685 -0.12289660476501649 -0.08478369732619169 -0.05276049066937879 -0.025621266447655174; 0.10866221020903608 0.22225751520339393 0.337037646740507 0.4433017614888372 0.531456507212767 0.5937604159181038 0.6279855729333698 0.6426005795878931 0.6530754799803088 0.6711070516251787 0.7011243930914303 0.7416918524805687 0.7862433914740891 0.8290375192823465 0.8702939459799 0.9119339147298914 0.9512850987820477 0.9773331519533343 0.9713310614941215 0.9161005893319476 0.8076063741599968 0.6576095790844219 0.48519931858716964 0.3048027140740791 0.12276195407777772 -0.05851417800948782 -0.23786461675641754 -0.41163487830311585 -0.5708455508128674 -0.7043452854712579 -0.8003817091369737 -0.8463588019298582 -0.8393482370570002 -0.7911005474993442 -0.7182187344265794 -0.63385738738869 -0.5499220799078083 -0.4764782837995869 -0.416483803599306 -0.36695616323156716 -0.32270314136951894 -0.27627302225985756 -0.2244291409320293 -0.17243158342807094 -0.1253882589708264 -0.08439906019498113 -0.05060810219988146 -0.023623201735654287; 0.09262810410732054 0.1946004785961522 0.3031342616047077 0.40547117234991414 0.49163635930552146 0.5591001275728371 0.6067129434178287 0.6326767899794304 0.6421952260311982 0.6498396508887772 0.6705603729428009 0.7120911887276742 0.7730442035364847 0.8454041886187823 0.9221195453448392 0.9999197343607619 1.0750469325420595 1.1366316002045873 1.1650330630152252 1.140212149604562 1.0525897124536359 0.9089971681428399 0.7285480198055614 0.5307045479095664 0.3280668241984667 0.12794287247903938 -0.06703511468192586 -0.25508201573706635 -0.4296544791155203 -0.5810843273021536 -0.6976827688799704 -0.7657911960785102 -0.7805934112308685 -0.7517960516027328 -0.6942934030989543 -0.6209496975870041 -0.5454138001469927 -0.4791924818178728 -0.42450550182259267 -0.37715262168891994 -0.33144443960290687 -0.2806753547189648 -0.22411243807049178 -0.1689746282882985 -0.12005768597667507 -0.07783963524278888 -0.04420117827058665 -0.01957142822059729; 0.07775017114279797 0.16626838723176535 0.26421971969671676 0.3592906775715199 0.4408809003915226 0.5078263614567026 0.5628215333715353 0.6030043759421411 0.6236726012225636 0.6315733438779491 0.644481126607102 0.6777311746936462 0.737228020971366 0.818076378287839 0.9093608142317061 1.0025553725404535 1.091169996379502 1.1651641146582428 1.2081192098691158 1.2027451031105696 1.1376486856892853 1.0131778678747339 0.8426478910086939 0.6441152985757831 0.4332250579149989 0.22229009516092582 0.01778817678355907 -0.17770625171357876 -0.3581809163347614 -0.5145344523266234 -0.6362675378301094 -0.7107394246392237 -0.7323409913938423 -0.7093542383243922 -0.6566761612657904 -0.5888054758819778 -0.5202257928514522 -0.45989402560956266 -0.4074664419653249 -0.35986133573728163 -0.3137193610393826 -0.26345843365039334 -0.2084879078128638 -0.15499047333767932 -0.1068279491175574 -0.06561754641339691 -0.03489416367673993 -0.01476247148951922; 0.06477455419021344 0.13782575117581514 0.21988850994631967 0.3034238271874228 0.378961820125746 0.4425800766375915 0.49669808658615977 0.5422771151898249 0.5745371916855245 0.5916575675436438 0.6040737758172094 0.6276668123416559 0.6730229803079042 0.7414519149620478 0.8247494352049773 0.9128025054171 0.9968702865780786 1.0661191732836512 1.107439017639325 1.1080920886323835 1.05859848433363 0.9563117186692461 0.8090786857848857 0.6298374494891078 0.4322718635381986 0.23016911260137787 0.033238397916135816 -0.15369112478315103 -0.32397635853121487 -0.4689307731597571 -0.5796019867187139 -0.6455277452844038 -0.662397328302374 -0.6385888323476544 -0.588710379148209 -0.5272642467123695 -0.46674734688000435 -0.41206040296369245 -0.36164208281546106 -0.31528992122725197 -0.27248173910987333 -0.2281524331354609 -0.18022532582470777 -0.13253135253940218 -0.08804848650541325 -0.0501226295147772 -0.0241069281446535 -0.009562283384033888; 0.05297961787444163 0.10979127459608436 0.17253889437768125 0.23905572951724285 0.3032568192947459 0.3599003514586622 0.4080784274289902 0.4487083831733067 0.48107211918986215 0.5033980948714829 0.518868529969746 0.5376580524506639 0.5695207080326158 0.6185265505756148 0.6813320844076944 0.7500436202532661 0.8162834042361492 0.8693756739632061 0.8986392373929839 0.8957385532209897 0.8543712989110229 0.7722474931071531 0.6540762095159083 0.5080916352037848 0.34368650328399736 0.17291512185781457 0.006210149191466668 -0.1503716928955276 -0.29081455622820757 -0.4078270431429915 -0.4941063435298682 -0.5419262833677918 -0.5496736439720846 -0.5256401111497242 -0.4818045714107471 -0.4297702899476773 -0.379141696794543 -0.33312924357302115 -0.2904430193211589 -0.2516620238747425 -0.21661554275692024 -0.18080345702370806 -0.1423746556955223 -0.10386386819932406 -0.06684084241805786 -0.03490433702564488 -0.014388067438330597 -0.004981172497829307; 0.039392464571378086 0.07944308613896545 0.12227644735645721 0.1681164896643823 0.21409080564879163 0.25685131375160575 0.2941881819248078 0.32439792254966604 0.3470204604612881 0.36335987085845717 0.3761303200723833 0.39081263939529026 0.41343140660294636 0.4464735714380679 0.4885518346498676 0.5351292752643451 0.5798763491712207 0.6144272325767303 0.6307747352667458 0.6239755557648786 0.5904870773061509 0.5293585310947758 0.4440259628706307 0.33995406374204035 0.22305960326579902 0.10193209354615784 -0.01525518314313442 -0.12397984236280879 -0.22072060361711057 -0.30061722168219335 -0.3580038850445556 -0.3875464542020051 -0.38947485747767085 -0.37034816999569514 -0.3380455669894274 -0.30012879465804143 -0.2636636709163838 -0.23163752947024427 -0.20281511831701488 -0.17633042500455645 -0.15119962899820558 -0.12484347308735984 -0.09742214411740685 -0.07083083271479777 -0.044894314019976546 -0.022018084865523497 -0.007807133532954638 -0.0022684512912463377; 0.021450550187885834 0.04269812293704475 0.06498305838329932 0.08850477057251774 0.11210439809304444 0.1347644378501691 0.1553213903994518 0.17174639512441517 0.18262957043226 0.18932657450180232 0.19495680162977927 0.20263781392739516 0.2150824326873778 0.23287373573992795 0.2548699712326381 0.27919963342389253 0.30248802550973486 0.3200714437512785 0.3274790863439058 0.32224897075499215 0.3028503934144161 0.2691059727296685 0.22329831956563698 0.16860472115485273 0.10821841038111525 0.04648399153684146 -0.012414957762169863 -0.06661571093120032 -0.11503248027033262 -0.15541701853365272 -0.18434262153367545 -0.19881757993632376 -0.19927561425221882 -0.18926465879148838 -0.17260856820117937 -0.15296463734548202 -0.1342911453969469 -0.11854319669928277 -0.10471686792999885 -0.09146633217002835 -0.07790749695835095 -0.063407476328123 -0.04898734641343615 -0.03564210099155827 -0.022592966921991524 -0.010871114770803565 -0.00366395014273333 -0.0010245916721617094], hyperparams = 95.63865982042415), (params = [-0.008550693633955336 -0.018427443287720342 -0.030403964046368876 -0.04403587525101972 -0.05824868799844914 -0.07247876847951172 -0.08548125342424949 -0.0932709601700671 -0.09065016430373231 -0.07500913939390569 -0.047211665346719806 -0.010378753631655791 0.030102851922307255 0.06754358311490401 0.09702065138008377 0.11708716195453044 0.12749925027543235 0.12820103211752829 0.12069677132001022 0.1079304653213965 0.09293569612674475 0.07779447142464259 0.06356102356027035 0.04929134328193271 0.03213061759033511 0.00872927743207696 -0.022531935501674066 -0.05980652800823544 -0.09783271493799639 -0.13121530619312755 -0.1570188907746798 -0.1753940296986536 -0.18753475865982155 -0.19310319992968383 -0.19160662209165882 -0.18489455423216067 -0.174238326495042 -0.15783595712936418 -0.13380912692536454 -0.10339653527439654 -0.0690693192667095 -0.033334941314564034 -0.00048335647055859334 0.024901137463346767 0.039963517506881104 0.043146220365219055 0.03512920651755234 0.01931883663852062; -0.01657631114988028 -0.03568619066328946 -0.059291314022477656 -0.08687366183540463 -0.11546654788685098 -0.14174501147282928 -0.16167300220460237 -0.16881966119470088 -0.15655940601996846 -0.12235362391763105 -0.06882936390160188 -0.002308160531197377 0.06810727639067146 0.13221757506495463 0.18256361664347345 0.21637234124626037 0.2330469285717392 0.23303498883630308 0.21931710989716008 0.19720564698462292 0.1716394350682112 0.14575326167780434 0.12080841642762206 0.0944079578945803 0.06131915131478178 0.015766385504798183 -0.04466888958025447 -0.116312477915788 -0.18945210935662354 -0.2534058095445775 -0.3017836000271594 -0.33454258519154934 -0.3551736182544797 -0.3651179358903908 -0.36333131682659503 -0.3505018430396639 -0.3279572249133986 -0.2941233810182549 -0.2473388257713465 -0.1892000552600284 -0.12336599186292596 -0.055409968877382774 0.00593362122234621 0.05220038678515038 0.07879784984258137 0.0837796544277603 0.0682126096758165 0.03767067983754794; -0.022696191391277945 -0.04972568810156402 -0.0843713620493913 -0.12537158334235057 -0.16660782430474042 -0.20046803601209642 -0.2196135933165868 -0.21745569581150073 -0.18975414255657638 -0.13612194044109785 -0.06107276657489179 0.026122452717293826 0.11384118959508739 0.19058058026664898 0.2478069564095273 0.2823672868879254 0.29521034613812897 0.28924689801012926 0.2696199946438411 0.2428979070927709 0.21347219586130162 0.18371594674168656 0.15363564270460572 0.11950794628357767 0.07487020339429587 0.013323087982029816 -0.06747445995332983 -0.16274426887648027 -0.26068893164889134 -0.3475914292434757 -0.4143155758037706 -0.45950252671856584 -0.4878077014415517 -0.5023355327132814 -0.500898484546959 -0.48122834497664846 -0.44423785832169366 -0.39122688033619735 -0.32310467345305277 -0.24166189593362514 -0.150346208901888 -0.05690449273031084 0.026216289966160506 0.08719947062349752 0.11990168661132099 0.12304447116197247 0.0990306223505097 0.0546969886655027; -0.02548634808172982 -0.057514628962021475 -0.10020834277808571 -0.15076234421641108 -0.19967889235299843 -0.23538993786409065 -0.24826696681012106 -0.23341758359027093 -0.19040771444399693 -0.12135629694618913 -0.032825105372575464 0.0631989236960799 0.15342999684224004 0.22602132257089425 0.2730656320999658 0.2941913757000105 0.2947084727817422 0.2812101540742483 0.26069532854658556 0.23791875488519304 0.21377266871413278 0.1875221838519109 0.15673120816848532 0.11782224704947353 0.06529488931357967 -0.005577076002880108 -0.09599085467071936 -0.2008413321411153 -0.3087291231343534 -0.40635057241804556 -0.48410264418921467 -0.539085916027718 -0.5743328412633727 -0.5926609029904624 -0.5906851642131474 -0.5635835485694655 -0.5112912937873155 -0.43800286592498316 -0.348758345302588 -0.24740382169569347 -0.13803311862183054 -0.028821984319540122 0.06717533365147203 0.13629800577547893 0.16983558685112932 0.16640555112995428 0.13077792734969235 0.07159787759436673; -0.024758046264675225 -0.057384384237104714 -0.10222341276094807 -0.15527195179882763 -0.20474377926132376 -0.23666010906659582 -0.2407497931220116 -0.21438051009992887 -0.16060833819265402 -0.08508029638166813 0.0024669019313459726 0.08888459767281208 0.16190231062528324 0.21244138416408861 0.23760729246679194 0.24267128898365217 0.23633543434825774 0.2266137853313513 0.2188432351191099 0.2123556876660173 0.2032168582157665 0.18562065659710578 0.1548810432599032 0.1094631303580129 0.047811545118216704 -0.031198749231872634 -0.12667888364081292 -0.23286205176004354 -0.33996939856186187 -0.4370059347254492 -0.5160735195986778 -0.5737399736514872 -0.6101724069604072 -0.626435906479561 -0.6198356159500952 -0.584959587745486 -0.5202968615140554 -0.42965865257849994 -0.32093029471466306 -0.2019171245687779 -0.07978085279063749 0.035939256195756275 0.1341640057726722 0.20308940308935922 0.2321416932952479 0.21810535957137986 0.16723128250450292 0.09041351133625915; -0.02131408336684581 -0.05057730377395434 -0.09195445213276536 -0.14066263597472276 -0.18385264541520646 -0.2072881953681611 -0.20173132565740734 -0.16674029147667677 -0.10938734610200627 -0.04029958823993126 0.02892999829780274 0.08789774202884962 0.1297339892494426 0.15297597542293512 0.16238286964386517 0.16602961357751136 0.1711121434528837 0.18259992505363729 0.19958998108681444 0.21621040575719283 0.224526009448312 0.21393495104414842 0.17883637291198806 0.12031989880914676 0.04336593282066078 -0.04804666159154808 -0.15004063865550257 -0.2557078705557128 -0.35700702086375674 -0.4460544229297716 -0.5177309436270714 -0.5692805042705046 -0.5988880769707392 -0.6050615100682397 -0.5869291259007974 -0.5416268137610957 -0.46751430561359164 -0.3663415389995347 -0.2447556537923025 -0.11312934694462569 0.01775801550284207 0.135129572390171 0.22772008527282803 0.287503143910003 0.30572809290220576 0.27756333757796897 0.20880841949775578 0.11176676410967169; -0.016148169224333837 -0.03969796861830501 -0.07408075777120011 -0.11353667305420406 -0.1451170782869293 -0.15625439766590693 -0.14039995037082234 -0.10053844052499387 -0.04820479113145155 0.00352496300746083 0.0455522939435839 0.07395407751784112 0.09082155604177151 0.10335165755036531 0.11953704780965063 0.1434599939083865 0.17667121207578027 0.21809690942928245 0.260633502206129 0.29569403651754245 0.3123120251287191 0.2984168991703433 0.24836342137457404 0.16608041847290786 0.06341097653319573 -0.04921201351248878 -0.16316750807193553 -0.270755698530371 -0.36504879901576637 -0.4419920130792529 -0.49968796241819324 -0.5374832903265895 -0.5529347156710355 -0.5426304092980605 -0.5062538677374295 -0.44521901684005916 -0.36031556069532056 -0.2533227748994779 -0.12780347244841764 0.007586851478600292 0.14070693966201442 0.2566118453273334 0.3408334040807915 0.3858535098535694 0.38717801287255027 0.3414743325926623 0.25319306261261615 0.13448423419064306; -0.010744102281530459 -0.027417670015723677 -0.05195947536354493 -0.0778904490787481 -0.09350830098738182 -0.08965562439548101 -0.06414958794250165 -0.02357761072383095 0.01935070894298958 0.053506887606530454 0.07513846161082373 0.08891692690463565 0.10526156445094918 0.13446386476392141 0.18040998654604568 0.23898679003147408 0.3045032065360822 0.3716806980879808 0.43171690195327056 0.47237581040588317 0.48071217149495865 0.44729470343267574 0.3682550470461538 0.25140140968466695 0.11257482160053266 -0.030878354183112723 -0.164588738669978 -0.27948291537149067 -0.36980007297344625 -0.43442533697863206 -0.47508677169334984 -0.4943057923481468 -0.490819342527678 -0.46025070196724127 -0.40205731630250324 -0.3204869732176126 -0.2199081008608503 -0.10505068755929936 0.020574678382913672 0.15178332450495807 0.27865417808658133 0.38733109230851503 0.4614278594634119 0.4901874263176443 0.47129112696116277 0.4055774107029997 0.29735122949583914 0.15716052540826958; -0.005884984731223331 -0.014523518001325003 -0.026011132276259858 -0.03445371069276905 -0.03130383647956818 -0.01216776464467406 0.02115784157339477 0.061569562042559534 0.09865440908387428 0.12513753335683062 0.1441731151720033 0.16796234735937066 0.20975340138332096 0.27699769718540035 0.3653296268701237 0.46111084536490043 0.5526604334801003 0.6345117927549903 0.6980829424713294 0.7268716306769739 0.7081752293775422 0.6375939884998857 0.5180190060143132 0.36126898406775587 0.18352125579784706 0.0053348118012320825 -0.15456764824951533 -0.28373836524010143 -0.3764672062373124 -0.43212168979085314 -0.45584407725381076 -0.45392855579110764 -0.4286644638361255 -0.37649968966474373 -0.29671472642274965 -0.19493167175138032 -0.07642329931559347 0.051808048134155085 0.1821986757218053 0.30870712879750845 0.42401913368104027 0.5187864156698788 0.5790913766941048 0.5916013309836331 0.5528562278903254 0.46677426453153475 0.3389720942592667 0.1785292204683099; 0.0011831198156515151 0.0032204060613001354 0.007647554410978299 0.018762414605275043 0.040824855235091446 0.07384515812961907 0.11465882869669423 0.1578159691735421 0.19561433760196575 0.22583680505207934 0.25822171664423366 0.308598004323181 0.39019307111667373 0.5053833840888993 0.6388827293182061 0.7681353659258445 0.8781139783941767 0.9620906198127247 1.0107828638347076 1.0093015982869884 0.9485764474440898 0.8307850860269227 0.6680592696802162 0.4751302703399263 0.26655861651157314 0.05921337317261196 -0.12817797578394685 -0.2800701030668541 -0.38669353717858684 -0.44367310494699286 -0.455816579746151 -0.43324855300797144 -0.3830707736787194 -0.3070095947543642 -0.20542359660984055 -0.08560716182576056 0.04764418907339828 0.19039938107932838 0.33217717072075786 0.4611751597975481 0.5675546329144866 0.6460057362817365 0.6895186921156903 0.6859623267140093 0.6296207165069327 0.5247372768734577 0.3780261561393355 0.19831867086964655; 0.014027312503264337 0.031035323025199044 0.05328490293150656 0.08333633525710882 0.1222419885486233 0.16822594870137692 0.2185259111185694 0.2681936040241616 0.31101374404813065 0.34896957615962765 0.3959451667101256 0.47173689367185967 0.5913875756746757 0.7506512905340946 0.9241546215030731 1.082002294753238 1.2031896113529499 1.276820592844262 1.295633621000552 1.2529291548013106 1.1469346697229115 0.9871842208199194 0.7921163821775111 0.5781210248867551 0.35626550753991126 0.135571879421287 -0.07147712712859187 -0.24942831732398554 -0.38326213303719875 -0.4605387659131315 -0.47771285885982434 -0.4438734941030344 -0.3703194338214461 -0.2675228423628091 -0.14154057237621664 -0.0014020720336009435 0.14531448071838735 0.299167558945845 0.45365660201535374 0.5923610828386826 0.6982030472414326 0.7644308995313033 0.7912730661072951 0.7723521475656316 0.7007328072927558 0.5790287096646645 0.4145407908651096 0.21666577314716984; 0.03203724713369691 0.06745229558756295 0.1082369123040308 0.1555795099409223 0.20956026030010624 0.26946663574344326 0.33306860497738233 0.39310783804195454 0.44113698615097274 0.47965006568777 0.5272246495179465 0.6109552775324496 0.7478109300421112 0.929819054659247 1.1276972793518312 1.3040947141055486 1.4283383199154795 1.4846536198223323 1.4704054434207616 1.3889770427083976 1.2474804996297673 1.0629125198825307 0.8573551315481226 0.6471249088807481 0.43718838206087224 0.22634097656058388 0.016065519622104858 -0.18191648515694725 -0.3484612520090899 -0.4633357710609119 -0.5085696206773714 -0.4821545443675549 -0.3957606995327958 -0.2686205119988593 -0.11696392146199114 0.047477975282237066 0.2129204521172434 0.3778110562186029 0.5422391356592026 0.6927228341127236 0.8057395570498835 0.8675268592609892 0.8810496073217167 0.8479191206729098 0.7632021597989777 0.6272053621763654 0.4468635457806213 0.23273292406666768; 0.05211912182205603 0.10715314167167482 0.1665717847151644 0.2305243228108093 0.29962189154648694 0.37614381282561793 0.45836492995293265 0.5329606943465791 0.5831746945958501 0.6090866396652576 0.6358339861487672 0.6980032909963033 0.8162573652324174 0.9866710169561288 1.1814448179471095 1.3599515727444333 1.4837604908313735 1.5280796591896384 1.4900333221276167 1.3812660566975015 1.221691928451275 1.0378854285779193 0.8523742801853577 0.6758453074480252 0.504139234398254 0.32559486517311814 0.12932743076893427 -0.07993985695904138 -0.27877920454539884 -0.4396725565310267 -0.5315765924295476 -0.534531190737079 -0.45368638877448264 -0.3129556318491094 -0.1389286216561243 0.05083452583782341 0.24107102063315675 0.42377415708038485 0.5986609203083512 0.7589955134394155 0.8822530685064331 0.9470420160543299 0.953510009931636 0.9093100709074854 0.8138001077497922 0.6663600444698974 0.4731618749418718 0.24574964709648273; 0.07367377760373708 0.14857457114174374 0.22559206705727344 0.30463739566689746 0.3883968029458324 0.4839437664346685 0.5897741820371274 0.6827106929886071 0.733268711913509 0.7363733894614511 0.7199107176532344 0.726223348130044 0.7882405890860572 0.9132467998561096 1.0796572528725772 1.248610069859226 1.3733230610352252 1.4163069025052357 1.368535135739921 1.249438324352161 1.096515942060931 0.9459206930760623 0.8153052772063427 0.6998255485124524 0.5822154935272383 0.4442635825592008 0.26863976011877766 0.05378390479452199 -0.17433684775163052 -0.3791071604320146 -0.5228473456077982 -0.5724904512062388 -0.5221667644658718 -0.39117980855428325 -0.20817696458346927 0.0027754930953239197 0.22009030682219652 0.4282957402820485 0.6207679386461217 0.7920101845975018 0.9250139194828396 0.9967890982085206 1.0028192982342083 0.9527090067772385 0.8496822959213457 0.6935908085702401 0.49091083379091593 0.254343213402917; 0.09621454880283346 0.18951362523547502 0.2796861709748322 0.36805049841065907 0.4618143617110849 0.5745084586560315 0.7051783974322096 0.8205209325484143 0.8767409894474512 0.8581363018630259 0.787980565779812 0.7171767727003817 0.6988082481078385 0.7558821538482771 0.8760822510664525 1.0234324269102046 1.1447087062593033 1.193972841978908 1.156438309256671 1.056370500632173 0.942640541426729 0.8545432531049364 0.7990897359810596 0.7513697820078156 0.6813419749630633 0.5690223813935184 0.40293609757580945 0.18105507886189767 -0.06867308565040782 -0.3024642437938146 -0.4820609528661868 -0.5761281990363397 -0.5713911811117452 -0.4754824349985941 -0.30794541926383784 -0.09130976453384397 0.14755127847365712 0.3839185905060825 0.6013276167249213 0.7898501562775337 0.9353061371435741 1.0162641631942944 1.0257009668918138 0.9734809216940336 0.8658360704960757 0.704306434426144 0.49658877953480574 0.2565298863926259; 0.11522407798527873 0.2217382499449443 0.3168928002755305 0.4040608280688506 0.49696549365201936 0.6172454045473403 0.7668155793963373 0.9055408006766823 0.9767546243797585 0.9517395789613764 0.8451674385604568 0.7110157113984308 0.6158381548791345 0.5964814106514659 0.6529083678764293 0.7568045865348131 0.8585180936048672 0.9162235218160362 0.913360542337921 0.8681049745805235 0.8248361001751067 0.8157933256237014 0.8344203917250065 0.8368374278845858 0.786747272871221 0.6719108981537688 0.49058380184167705 0.25025848089070957 -0.018580658810486494 -0.2690442676590296 -0.46328858390442934 -0.5820633652373363 -0.6142519799321148 -0.5552877931108349 -0.4136592917563148 -0.2066969058596417 0.03991343589788462 0.2974419242629895 0.5400271824970111 0.7498460870046189 0.912739845563789 1.0074047784966804 1.0233184275180793 0.9707778778022637 0.8602529856044686 0.6964564535760328 0.4888554737751433 0.25179389079542985; 0.12561503989765826 0.23689774501125274 0.3271599464543697 0.4005411137119863 0.4770261779350252 0.586326446227298 0.7359092502100929 0.8867778860939949 0.9778455290215263 0.9698690215785092 0.8662670967136139 0.7136244095117722 0.5745008607112133 0.4903977784113356 0.47588202505124577 0.5164976354049455 0.5784454004629155 0.6377151621185063 0.6801968873861886 0.71172401819489 0.7571859890498367 0.8332816391183199 0.915940925766748 0.9470110455896472 0.8932945127852433 0.7538574807596037 0.5304056923815241 0.25840561495642483 -0.03322382342841796 -0.3046464829945958 -0.5116406361095945 -0.6402360794487428 -0.6923641035201085 -0.6572671412418819 -0.5308158504897207 -0.32836876749260974 -0.07759067236427164 0.19293958313754536 0.45443193961517037 0.6830132277065994 0.8634381287973648 0.9744873381961281 1.0005833257892542 0.9499565186878297 0.8380187701791331 0.67457613497834 0.4710599668288106 0.24179450868963945; 0.12473507681142931 0.23161666189599006 0.309120649294118 0.3592096538264049 0.403833300156743 0.4775938110335341 0.5974283252821376 0.7360714143282427 0.838220075707825 0.8608733100871192 0.798172178931662 0.6797903748281878 0.5451922521409757 0.4271375650748225 0.35300240974235847 0.32815288114766183 0.3424493289968388 0.3920175939229849 0.46965861366784883 0.5734982591741504 0.7075777286321011 0.8668872245327762 1.0028327977342404 1.052783998618044 0.9882668936812784 0.8028554043231778 0.5133528156634816 0.19943653271945178 -0.10659483055151825 -0.39486426387467316 -0.6227389648472887 -0.761444676496841 -0.8216916625552253 -0.7984177759813335 -0.6756391448529002 -0.463812761957156 -0.19806181149991647 0.08856635477620303 0.367235875083968 0.6116392064263584 0.8060075594490532 0.9306573756218455 0.9672181275642551 0.920827902680411 0.8093536740282171 0.6474252639858212 0.4493216071235785 0.22965330706372164; 0.1130377125162856 0.2081589087238865 0.26991963818150916 0.29491187281782366 0.3005643685863784 0.32168303423935407 0.3861441685023998 0.4834645239181242 0.5723473813466967 0.6177854779065305 0.6111238949641494 0.5602033787669778 0.4702263544455214 0.3544606409356526 0.24795759456765015 0.17650096555956038 0.15130213784353796 0.18251920685792156 0.27328805616978213 0.4242212485722997 0.6296993894120082 0.8631518250482197 1.0521380068935382 1.1211607599360363 1.0379304880933256 0.7857677598614179 0.4212915244447912 0.05825392137275614 -0.25382578294619546 -0.5349775018733516 -0.7700158513440233 -0.9188344115733599 -0.9843140795792323 -0.9660550774255785 -0.8411356064629925 -0.6124909121308412 -0.32173807189467135 -0.010884471119015391 0.28921679357611957 0.551466531040479 0.7591759140456747 0.8942334252952069 0.9387772918639401 0.896773398321894 0.7869386307893298 0.6266512368748498 0.4325628870239699 0.22013818584079287; 0.09290946775896103 0.17198115180550283 0.22103175005603484 0.23056404667406563 0.2074583984690922 0.17878319437017184 0.17849970055691056 0.21351994346978756 0.26141264887731647 0.3032994446275031 0.3368365184859819 0.3547306395229837 0.32762459841690056 0.24114978561638675 0.129550937703356 0.033636727181501375 -0.020057335746055418 -0.011806204090630467 0.07235388145400466 0.240092889086315 0.4842703180091718 0.7712405249388926 1.0097035594978159 1.0993589643313366 1.0055241463130387 0.7167155172230897 0.3113195306660658 -0.08617078562812144 -0.41703776678924687 -0.692357310614588 -0.9178492132593767 -1.0660499424426313 -1.1354946157465047 -1.122042425113484 -0.9965658508700679 -0.7540093888059141 -0.43821800085476986 -0.09954324556767016 0.22591533141774636 0.5085679487385923 0.73120762301182 0.876888518515275 0.9288891459990404 0.8914830919833456 0.7836491768632468 0.6239201144532354 0.43030745279326277 0.21882132127666937; 0.06664213067080987 0.1273665324052858 0.16982159581013193 0.18069442826717128 0.15359283132802662 0.09941777266749822 0.04804007877430283 0.018806796289807963 0.00895125110994108 0.01844354640997839 0.058138668959675205 0.11730952646691303 0.1414210951889232 0.08930833165760046 -0.012955544114864648 -0.11727124219304774 -0.18622338042039077 -0.19732170801783142 -0.13513905714272034 0.011571744390493527 0.24712409473279193 0.5465350547479833 0.8134146351263978 0.9314147035254984 0.8662145832251817 0.6134940762344325 0.2295135852942136 -0.16269867756246756 -0.502482653860265 -0.7845036210135943 -1.003195918179283 -1.146524485811099 -1.2211824673914888 -1.2172648482152806 -1.098838789601923 -0.8549439958438266 -0.5266120488334464 -0.16693859750971285 0.1824688879760629 0.4865450853113983 0.7251027953227951 0.8820272293229092 0.9423649228015114 0.9106238080902644 0.8052155608159944 0.6445318779059233 0.4466761374487947 0.22796536951099394; 0.03441341339998833 0.07318265586701181 0.11165041601618833 0.13647620620819284 0.12973136164286073 0.08322566283154077 0.014007530351396598 -0.05649910085458943 -0.11729306772012241 -0.15326843627791864 -0.14125711978389915 -0.08609577485044208 -0.0478616115789334 -0.08097876040905007 -0.16998533101770516 -0.2678364561800298 -0.3375461371880098 -0.36583034910145584 -0.3454225582247941 -0.2575844904542562 -0.07517249551447099 0.18922915288933273 0.4653614106923835 0.629649522781259 0.6280534874903136 0.46310981145516217 0.16037934680495597 -0.18488880075089092 -0.5065130417863681 -0.7776935795463034 -0.9821651204336396 -1.1182675292676687 -1.1994835967684594 -1.210082723176582 -1.1087177964894186 -0.8804446825054948 -0.5599360752770353 -0.19631139809998047 0.16569962635981408 0.48549144469182187 0.739101956842201 0.9081606089574238 0.9775204599320486 0.9519191223310729 0.8486664080501374 0.6849420882862165 0.47832176874712806 0.24549428792440994; -0.003378427598677342 0.006542824593309567 0.03427513460876773 0.07111909170450319 0.09422583637408466 0.08145145557606549 0.034053853899901995 -0.035661931678126015 -0.11600874165337952 -0.18707285387461145 -0.21941243089560916 -0.20677342750508085 -0.19482569366894417 -0.23218099299224457 -0.3114136528020901 -0.39573607891157647 -0.4595457968779009 -0.5080641651415231 -0.5425158636944061 -0.5273505780851446 -0.4250822634412461 -0.22535019756428107 0.054622708661457416 0.2935935191038431 0.3896550020434692 0.33482150067228394 0.13724058664694486 -0.13505175307279138 -0.4126727927411973 -0.6575641717304562 -0.8456439292771938 -0.9755633471932538 -1.0623094614263642 -1.0862160362487683 -1.0066575471805495 -0.8096111271823287 -0.5191057809590215 -0.17294018901024555 0.1843683121422822 0.50811455118303 0.7706126858647794 0.9496926619087749 1.027827211186594 1.0082374169917725 0.9063546353337832 0.737575025166341 0.518689057529841 0.2673795017480763; -0.045163544626725026 -0.07216969216370117 -0.06877520503853328 -0.0355398334329543 0.009225466684026599 0.03952313061485927 0.04264348642269747 0.014959607967323827 -0.044159455116573966 -0.12241901744380176 -0.19168710531130437 -0.2351478239854198 -0.2737065331087137 -0.33563831072386957 -0.41494142517225174 -0.486324566600526 -0.5390956122607382 -0.5988273209126569 -0.6767695169027577 -0.7273667800619362 -0.7057724029571318 -0.5683988613552583 -0.2872109456433431 0.023917445467426808 0.22295337184155084 0.27768583650191186 0.18945622986974112 0.0010366648891969735 -0.2188045254865672 -0.42976312437608305 -0.602731166440638 -0.7306261207224943 -0.8211072124387323 -0.853944862706362 -0.7970512099476005 -0.6411458052632187 -0.3989524046248342 -0.09169226359903297 0.24151780413520985 0.5550364448328703 0.8180769396716453 1.002120815373431 1.0854250536819046 1.0696652942508986 0.9677803537699083 0.7925922764605402 0.5601377393311273 0.2895329475232899; -0.0887448451010573 -0.15955731587402308 -0.19476368468087196 -0.18492357760538528 -0.1371080934131536 -0.0716771539768484 -0.009204749199093087 0.029861506994370447 0.024094597077347745 -0.03188662536693633 -0.11730033757443209 -0.20869273493066953 -0.3025633332215206 -0.39929348713193735 -0.4869294963980234 -0.5495812475465051 -0.5852727305633919 -0.6311996768230386 -0.7160657229927228 -0.7972579725813866 -0.8210590624087445 -0.7302848246964244 -0.46339945495086915 -0.12877353318527865 0.13412980895470555 0.2748166564407746 0.28350815223733467 0.17955486624128716 0.018995682145852896 -0.15819776350298717 -0.31468887649108296 -0.43198935508194414 -0.5117895818145756 -0.5433497734041799 -0.5078587465173519 -0.3983781270991431 -0.21359369585282476 0.041719623073022995 0.33577221122321715 0.626107941520474 0.8795098998356309 1.0603928989019238 1.1429303579913546 1.126840948738897 1.022349474054431 0.8399829502185225 0.5950366920330492 0.307880535565878; -0.13140033077622126 -0.2488766656667406 -0.33257707008165444 -0.36302021744399154 -0.3328933499354012 -0.2517142879640717 -0.1416348072580119 -0.03535666233920693 0.025116641806792395 0.011404369100714113 -0.0694581974768172 -0.19159421232704676 -0.33168750063053676 -0.4628314706001619 -0.559979627680771 -0.611630072474087 -0.6204025936706006 -0.6245110833759624 -0.6688688633473228 -0.7313792876519668 -0.7519167926808925 -0.6827811469316701 -0.4619883769641651 -0.1627899552543877 0.10990483038578616 0.29636570055964473 0.36923153689027743 0.33106052346735415 0.22371957855048302 0.08465975110623405 -0.044251498663130384 -0.13373363805666985 -0.1880882836133082 -0.21061319613917193 -0.19230323549941006 -0.1246534424939407 0.005997516325989193 0.20739886661406 0.45610918131412453 0.715718761336069 0.9509857972496529 1.1197229635125214 1.1939693545117671 1.1724289163645738 1.0622400181715967 0.8721317257581952 0.6175186155953226 0.3194166488174252; -0.17112449086344617 -0.3322459495708232 -0.4655890339299664 -0.5453322198206112 -0.5501464218097756 -0.4774096579426828 -0.34698158932730777 -0.1975894316466977 -0.0836262875177493 -0.052892645571917626 -0.11585600142411848 -0.25000874253891814 -0.41802847243453556 -0.5702140910104911 -0.6679627684767947 -0.702354050771647 -0.6760851113935752 -0.6179097856009509 -0.5804983025603413 -0.5760858208865863 -0.565374515270359 -0.5026549320214456 -0.34382736623350396 -0.11171747206000619 0.1286769813769802 0.3231767438140777 0.4279563386150484 0.43382854557439016 0.3726856061027058 0.2748729792038553 0.18096562459525836 0.12300322773437063 0.09375767102285718 0.08257306835741508 0.09245022699554134 0.13186372815139746 0.22245067108099054 0.37913399247999896 0.5855585134795215 0.8130290101705929 1.0243950608226426 1.1731164079232572 1.2325022107350057 1.2005287034028682 1.0813381274345855 0.8836155215350946 0.623737235161935 0.3221626007073573; -0.20771611812001362 -0.4065084805207693 -0.5830631739320088 -0.7108893776114624 -0.7591932980730142 -0.7155304533326196 -0.5962518061315382 -0.44083466392481807 -0.3056840569462396 -0.24763908049711977 -0.29178953172585786 -0.4229860839611146 -0.5985035220713405 -0.7558734739311296 -0.8454606201092928 -0.8563728230029545 -0.7904387783760973 -0.6657637068886473 -0.5315982222876661 -0.4266348907761619 -0.35673145524104144 -0.2919346439810908 -0.1888552178771777 -0.031082864190727037 0.15693039238124104 0.33905519739072176 0.4644605444079615 0.5075510021031646 0.4850900665775249 0.4200706991798075 0.35087572696389446 0.3094826317711672 0.29253416593357695 0.29158861468176484 0.30263900780648234 0.3321504547123986 0.40415988065297603 0.532533635305912 0.7070339583599257 0.9060499023923759 1.0902355482632313 1.2131929285287113 1.2526357533752628 1.2060521824610209 1.075575331896722 0.8715429028827486 0.6119370743405529 0.3153648673907629; -0.23921188029802323 -0.47015323833746014 -0.6829548493056249 -0.8524952128647414 -0.9443722510737431 -0.9416639497424034 -0.8578065030320126 -0.7288503956989114 -0.6055671501399587 -0.5439572960002773 -0.5774566445739695 -0.6980457292470691 -0.8640158111059507 -1.01293584407606 -1.0927224984879298 -1.085764591018419 -0.986182650805011 -0.8024645198629639 -0.5816496352073747 -0.3764208487222501 -0.22854880341644285 -0.14339168010555067 -0.07683167812382756 0.01679739013032318 0.1558479163843099 0.324347637550602 0.4671488558969476 0.5440950831148933 0.554860723672407 0.5107052975678394 0.4496752809791091 0.40801393684558906 0.39374461143752404 0.4010693918504309 0.4208107436232507 0.4586542389198448 0.5321367358966993 0.6491971619116018 0.8048712426926092 0.9816002349544266 1.1384129815931372 1.2332994463520515 1.2502784616553615 1.1866563287650125 1.0445019282668757 0.8374334457473896 0.5842556938841443 0.3003265434546142; -0.2613148643560218 -0.5180382617288581 -0.7618457638532663 -0.9677162756407252 -1.101341540643582 -1.1455666696963203 -1.1112077583640945 -1.0282290562328182 -0.9376189156338246 -0.8874148369126728 -0.9141837743557364 -1.0186289359646323 -1.165046471349473 -1.2976025878543151 -1.3673039077781899 -1.3519908748543397 -1.239424966616259 -1.0255006180324038 -0.748663371651217 -0.4726442141141544 -0.2574471301421206 -0.13819002441744224 -0.08060838046815914 -0.02145859746870406 0.08789882844894381 0.24800891227284505 0.4061100958978206 0.5082899812819069 0.5369967725765105 0.5014390954479508 0.4433912018332701 0.40331668520912106 0.3974916394605653 0.4183871969275456 0.4555583462666019 0.5127211858259141 0.5994330582006497 0.7192089134988653 0.8689432006873652 1.0293735097394903 1.1594395311936225 1.2267939617462222 1.2220245682077404 1.14212612192336 0.9912461889756314 0.7861240003123396 0.5446873337217593 0.2790014952162897; -0.2739220964382158 -0.5484730174144434 -0.8159556990612798 -1.0517159988552227 -1.2245139190139995 -1.3183226439601747 -1.339419820322623 -1.3096309355576181 -1.2595654449205025 -1.2260107124346231 -1.243528714016112 -1.3235407733674003 -1.4427600721875546 -1.5559926963624877 -1.6198204342609468 -1.609151060041222 -1.5100076425430289 -1.3114457067125984 -1.0321354446360593 -0.7329048366166785 -0.48203592158241937 -0.32511842894418846 -0.24782060509220963 -0.1910499814468077 -0.09918545990686016 0.043726257711461484 0.1977183675777175 0.3092617156980683 0.35398629152547684 0.34229645579807283 0.3115160477247676 0.2986327919696271 0.3186601198474939 0.3630495626969473 0.42402853894216364 0.5053720962583004 0.6125582860784616 0.7449364894933848 0.8954217040248168 1.0408858808917765 1.1461726345397245 1.1901650142582845 1.1667150678166334 1.0736266259863207 0.919155526303351 0.7214728212324931 0.496122041714835 0.2527965260541944; -0.28135184095778437 -0.5657600700180038 -0.8463013587122378 -1.1014116298128986 -1.3056666796635172 -1.4444689298215867 -1.5181898449525844 -1.5398375493757566 -1.530038432230222 -1.5130407862899455 -1.5176303900562131 -1.5661019226081634 -1.6521426896648443 -1.7432240971804196 -1.8054251011529696 -1.8161269453634847 -1.7590971615469773 -1.61927292849726 -1.3959931226586277 -1.1295769937781095 -0.8847929894056432 -0.7062285086018101 -0.594290651696095 -0.5080731707712729 -0.4077956749870811 -0.278598003176551 -0.1427512234347841 -0.03348867197005856 0.032096439992613336 0.0636561914029001 0.0847907161763524 0.1195945565344733 0.17863005173155924 0.2553997838697836 0.34625197811535674 0.4564992204248801 0.5882020176199577 0.7347829353818998 0.8843480459875488 1.0140604009566685 1.0978013762712981 1.1228339640148153 1.0844423581833995 0.9833291849182455 0.8319674591713601 0.6471977478752362 0.4412530852394925 0.22310682515769328; -0.285099352021112 -0.571666415631114 -0.8537321585090645 -1.1148497818908185 -1.3370303252672897 -1.5084705545350925 -1.6241397570770237 -1.6886538471540216 -1.7141981837002909 -1.7130339934412913 -1.704500567795189 -1.7187111013849454 -1.7693108053902864 -1.8376118004135895 -1.8980802343288556 -1.9359935312458911 -1.935833775154145 -1.8773489796808223 -1.7468675152413733 -1.558319872820933 -1.3577108429701115 -1.1853052444211853 -1.0520479833897227 -0.93772981248208 -0.8192996974136995 -0.6892254369283951 -0.5581198430640947 -0.4407009712786485 -0.3424462457972376 -0.25815252798657357 -0.1786033963114531 -0.09006194101929081 0.012943739667945937 0.12589023112397438 0.250457543125735 0.3915772812346548 0.544529318816118 0.698079597737726 0.8404534837249725 0.9528611856827669 1.0180544436748378 1.027895076103087 0.9785689668047413 0.8757693820271624 0.734398630749553 0.5673012735781824 0.3836237421160985 0.192432522022922; -0.281798162840915 -0.5623031198928918 -0.835900790558941 -1.0903720073421916 -1.3147131786166943 -1.5023770583329532 -1.6463235621164556 -1.743230751306497 -1.7974106681938566 -1.8127810436592813 -1.7984093524908729 -1.7834672693999836 -1.7985394319972743 -1.8440959412343345 -1.9020421770878546 -1.9620963376555143 -2.01233005982091 -2.028967405968055 -1.9913403528716958 -1.8951743428437866 -1.762103485843811 -1.6218074275048142 -1.491168190570137 -1.3679893750287815 -1.241843102201753 -1.1081381708507334 -0.9692441775904709 -0.8301910359365101 -0.6938052102932906 -0.5608817762434849 -0.4281364865195551 -0.2887758606586972 -0.1436614798714194 0.005675811807009066 0.1635807531731641 0.32938211945789625 0.49231675503003663 0.6435012170440109 0.7740427138706273 0.8688477582531997 0.9164407313585048 0.9112653904255646 0.8545739174469293 0.7572603590997438 0.6314558772844386 0.48503616013908213 0.32583945071441156 0.16257636957149235; -0.26921750451235127 -0.5346367586887806 -0.7903678852617128 -1.0275696028163162 -1.241020961221207 -1.4297547154919312 -1.5879377994600827 -1.7067078000751477 -1.7834545775834603 -1.8179524441876829 -1.8119561211289046 -1.7848236979303214 -1.7705484197989778 -1.7890901620779984 -1.837322388696021 -1.9074442570555479 -1.9896340239674344 -2.06024801482678 -2.09399221921868 -2.077331087972083 -2.014430314882374 -1.9233650279829015 -1.8195788710609757 -1.7077263478134674 -1.584509140099262 -1.4478979926709195 -1.2980279713702545 -1.1380639364967637 -0.9727570563625926 -0.804573749848276 -0.630524933103579 -0.44976100269103864 -0.26732038435160055 -0.08465831954403066 0.09915642731112823 0.2772033373017258 0.4401080334293313 0.5837046244633369 0.6987012396827504 0.7723231839567444 0.7982804365122684 0.7781633934938738 0.7208477907059814 0.6357912862214666 0.5278340943867763 0.40253228680824804 0.2685978021489784 0.1335198548657718; -0.24857409700139863 -0.48969528326645456 -0.7172900484186598 -0.9273620240465069 -1.1206680010417995 -1.300120042408282 -1.461272920102921 -1.5923463485973315 -1.6856140717787704 -1.7402237756314907 -1.755708858569179 -1.7390342466382585 -1.7140570490466651 -1.7086822153415144 -1.7368059357305776 -1.7984498268483116 -1.8861064733034174 -1.980644584668366 -2.056156429930622 -2.094321987074671 -2.0900673294983525 -2.052169931052469 -1.9901255554618644 -1.9059392650762448 -1.7970312958215673 -1.6639703716321637 -1.5096410330914138 -1.3391556545259222 -1.15822240176583 -0.9679782628861076 -0.7657002017075955 -0.5548547814538279 -0.34407590094624646 -0.1381474212093088 0.05887435828474486 0.23844361693459346 0.39556015887532686 0.5259310409822944 0.618604867743495 0.6651028885669862 0.6678393215711149 0.6384226513817806 0.5879396650986936 0.5180106828643603 0.42745696571131225 0.3225746909134947 0.21316376062394732 0.1052704868797587; -0.21982185804972448 -0.4281951699549347 -0.6195949961137446 -0.7957314374680692 -0.9629526914540764 -1.1262976632027308 -1.2825258870485101 -1.4194660682386737 -1.525133893516338 -1.5973943148092482 -1.6380574295985944 -1.6465392060124016 -1.6323075139376453 -1.61933975714207 -1.6296291060528123 -1.671940201737811 -1.7437324166304835 -1.832639986962998 -1.9175875240151583 -1.9802044513416401 -2.012753113904946 -2.0175589905883338 -1.9967703066205882 -1.9465958276312652 -1.8624949576139649 -1.7455917754838424 -1.6004999498523953 -1.433042706548638 -1.2482055921828095 -1.046682088916821 -0.8284065089291909 -0.6007636917598731 -0.3755777024543414 -0.16055420024263783 0.037275454771505165 0.2107398990035724 0.3558701240596112 0.46567559654818813 0.530523554110999 0.5498907862978979 0.5364828013217499 0.5063153694680361 0.465379357501503 0.4088294583443283 0.3345152665735043 0.24944198325477457 0.16247350418325898 0.07903894535844808; -0.18048585592126654 -0.3489395772713302 -0.5018280006597479 -0.6443749487225237 -0.7846302689799285 -0.9275097414360638 -1.0720186561021998 -1.2097720584059162 -1.3268689652505166 -1.4153922548819697 -1.4774401301815046 -1.5124102354092228 -1.5203823824262588 -1.5162503103820495 -1.5210102205943543 -1.5472924302784932 -1.597934741073934 -1.6669136561008044 -1.739752743629917 -1.8019811066291325 -1.8471717585484937 -1.8745162843787213 -1.8811323824962587 -1.8592404172313861 -1.8024443006637565 -1.7100623352877071 -1.5854598442689463 -1.4327359240939435 -1.255145289858316 -1.0544325380463173 -0.8342586415500343 -0.6050619644530252 -0.37968193127064387 -0.1678743444823234 0.021889833774275197 0.18294323751431907 0.30970824017613785 0.3946251042809745 0.4338632878714894 0.43646139331890293 0.4194685138827873 0.39420437846942846 0.3606487935143865 0.31408404214320496 0.2545308390006257 0.1874518275299167 0.11951590403055258 0.05663991020488699; -0.13081369661212242 -0.25419338810766295 -0.37003403592400685 -0.4839001133259761 -0.601088280067467 -0.7235095030790087 -0.8515816584027618 -0.9835510344919897 -1.109351064502025 -1.2155105489311966 -1.2976960222798977 -1.3555099125558898 -1.386944992027 -1.399335212874086 -1.4084341432157155 -1.4263857465233485 -1.4591575177649176 -1.5055797687458683 -1.5571394760944892 -1.6052387126475627 -1.6465251859954788 -1.6789370755138802 -1.697556849523135 -1.6938350357229115 -1.6601362103414403 -1.5933006083429537 -1.4944726276537654 -1.365235408878664 -1.2066240847407668 -1.020664031962382 -0.813357378961328 -0.595788988287479 -0.3806230803775884 -0.17973270461634608 -0.0030117593014295095 0.14192335466931796 0.24857457647014602 0.31256120788459624 0.3379052454559164 0.3381919465818175 0.32640859403540384 0.3072038262367402 0.2792020767931438 0.24086378443667328 0.1932941791102151 0.14008336288328008 0.08697867328308947 0.040047638192783966; -0.07738632574666274 -0.15440678684029893 -0.23442198707700643 -0.32220835376667434 -0.42000794667388114 -0.5260819003846255 -0.6388964857825018 -0.760047557669054 -0.8864368215778469 -1.0062904889740574 -1.1089995415905411 -1.1891449396200995 -1.2434383796055095 -1.2753656949512548 -1.2954498690040854 -1.313228091254224 -1.3346458826842076 -1.3606850490927391 -1.3876498287142205 -1.4136909251407632 -1.4402973228112226 -1.4665440394207534 -1.4873839824631638 -1.494927861956516 -1.480345674643825 -1.4381990390374235 -1.3675386525932345 -1.2676411466353261 -1.1369243663326691 -0.9763971728437434 -0.7924340102577897 -0.5950426544166542 -0.3967112082171783 -0.2107736262243248 -0.04854813909750574 0.0814980490098526 0.1738394253110725 0.22877799343125232 0.2544883424803313 0.2617346000622728 0.2575279733679579 0.24428192398902365 0.22225460545873102 0.19149983313487673 0.15286006681732414 0.10951713793115786 0.06716307026453966 0.030725362050584612; -0.029923405893668525 -0.0647952794952474 -0.11026365661360464 -0.17137968148182187 -0.2500666210364678 -0.34276089044347496 -0.4442979344453125 -0.5545607917808634 -0.674175169639443 -0.7973619188434465 -0.9139855866637288 -1.0134849763964247 -1.0886698269484754 -1.1405976541825829 -1.176278823285535 -1.2023355348858378 -1.2228109907860698 -1.2380426599879102 -1.2465627332017135 -1.2516503376405868 -1.2601122073201207 -1.274724469625786 -1.2925762814905708 -1.3070169010477 -1.308506585438684 -1.289381053106752 -1.2461634045982852 -1.175858077093667 -1.0747485346128458 -0.9429716086107793 -0.78609127949347 -0.6124289938080022 -0.4334095096970562 -0.26266320142830996 -0.11250560095922105 0.008227988339530423 0.09555506328839358 0.15283766607227303 0.18740138327893036 0.20441081342114717 0.20716927951754835 0.1989436447153631 0.18236982840404714 0.1585976796139601 0.1281686335600236 0.09337832201101333 0.058695320561815395 0.027642931842916645; 0.005268761127894516 0.0033308417621209225 -0.012256555210306951 -0.047388100646746006 -0.10554877086844391 -0.1834795362973982 -0.2739804870153955 -0.3740627590318417 -0.48415642625755906 -0.6024211823387227 -0.7225311933299524 -0.8330575247481707 -0.9232911633797415 -0.9916192765153332 -1.0423524316919217 -1.0794396274968028 -1.1056349954916376 -1.1208358189005139 -1.1239097961969648 -1.1195461528320334 -1.1172882848643455 -1.1233517040662562 -1.1380006126009425 -1.1565903413800733 -1.1702285556929881 -1.1696552711025954 -1.148598088315663 -1.1020029061980585 -1.0256139949711094 -0.919652339406254 -0.788430064406665 -0.6379176315460153 -0.4773853487970316 -0.3200663159687985 -0.1787918967275132 -0.06257583063895937 0.025534899109909814 0.0894727488193576 0.1337135518010872 0.15887448747849248 0.16622990233149865 0.16063074618321685 0.14776854656247373 0.13075594521797432 0.10949534387745136 0.08355129009455262 0.05503658757142498 0.026917485861513685; 0.027816925812918305 0.047587196562240267 0.05337283265000287 0.03984626927662452 0.002819174107964653 -0.05633263356030447 -0.13232269582652753 -0.22153815090855616 -0.32200479476501276 -0.4315943624310473 -0.5465478638150127 -0.6578918865262786 -0.754977763823514 -0.8340542356257848 -0.8963258909306004 -0.9427403339699806 -0.9753254684641908 -0.9952290127243104 -1.002125961929681 -1.0000288681217917 -0.9978207163723293 -1.0026687073682166 -1.0167940718977426 -1.0377483781665782 -1.0583309436492907 -1.069013974965704 -1.061510010564026 -1.029826545814602 -0.970896762287039 -0.8857218074006962 -0.7772441240368595 -0.6487292520873448 -0.5070239491570699 -0.3641026280973481 -0.23209932689660853 -0.11968794454879046 -0.03004705897489837 0.038973354830617646 0.08869969716051267 0.11735414892638757 0.12597152044382068 0.12127334593153712 0.11148476475799313 0.1010646222826715 0.08882823506471525 0.07155918607866754 0.04928236516174745 0.02482256358704042; 0.04035178184943164 0.07207913330186556 0.09043919522054 0.09196344068181017 0.07357530258878008 0.035248383202960594 -0.022309134780622786 -0.09886016117260761 -0.19039467147097056 -0.2908622984736167 -0.39575251680726387 -0.49869044821438796 -0.592090516222511 -0.6726227472480089 -0.7395729772003284 -0.7918058247398534 -0.8304470513320822 -0.8576155510949734 -0.8736773333913567 -0.881265625252169 -0.8868280025652675 -0.8963378824147505 -0.9123649148752151 -0.9339853733141649 -0.9559931734117988 -0.9697647978291702 -0.9667331239375156 -0.9416999616869155 -0.893684123959543 -0.8245463151259979 -0.7359243254335264 -0.6288606840535326 -0.5079166518457237 -0.38274581979713607 -0.2635983105733586 -0.1581930917206971 -0.0705201481681664 -0.0013077929134475586 0.0481404628005962 0.07556879797953206 0.08325444887312723 0.07939388329448081 0.07288976268724019 0.06817384591208119 0.06336092227746648 0.05392424412042569 0.038662346190099554 0.019958795528361148; 0.044894131795133636 0.08140637063645838 0.10605666555497047 0.11670405110736444 0.11133433820070905 0.09021047515112439 0.05156204487354362 -0.009000746780621021 -0.08911369884799916 -0.17981034841095908 -0.2736165387911234 -0.36411514358671554 -0.44558466808724123 -0.516461904084524 -0.5767501969579565 -0.6260748733004612 -0.6660527909293802 -0.6990993533047692 -0.7253567376543716 -0.745251926291251 -0.7619077853126496 -0.7789241105050326 -0.7983265360214382 -0.8198771399644967 -0.8399495803132221 -0.8514337770316304 -0.8473018560828602 -0.8244924536469188 -0.7839435485119143 -0.727792467568365 -0.6567959461626769 -0.5706825955762342 -0.4720380378642862 -0.3679605094612207 -0.2667515580542076 -0.17485617454850733 -0.09618878203632261 -0.032964594373316156 0.011971800699356126 0.03612513886903863 0.04244886568001246 0.03946999318559719 0.03554673961079114 0.034702253163400316 0.03522608918860664 0.03243395963681916 0.02443830597184102 0.01296196664401296; 0.0419398708584622 0.07721545715807425 0.10347926525480085 0.1188245355364047 0.12094664602229123 0.11033086551927411 0.08601966512025039 0.04277871531753082 -0.020138470114086832 -0.0956723411090536 -0.17562453780684326 -0.2524144519543314 -0.31962060524691527 -0.3756975288088562 -0.4219032147021958 -0.45973539662209206 -0.4922426672703028 -0.5226865637179986 -0.5516671692003129 -0.5781046233184879 -0.6018796701904545 -0.6238272629022907 -0.645020100229572 -0.6654528601971637 -0.682454695838294 -0.6906312924284808 -0.6852739435927767 -0.6654508264494787 -0.6330072383817564 -0.5898208769600469 -0.5363688734469403 -0.4719404780893172 -0.3974447374118206 -0.3176869531494309 -0.23935317362196806 -0.1675211494572739 -0.10470886359376541 -0.05257683991455991 -0.014559064262820016 0.005967444774210831 0.011244620971932576 0.00884740923731301 0.006175734262604882 0.007166941353324869 0.010768561410498994 0.012651136387072676 0.010615777743799137 0.005866911069672442; 0.0320978640525614 0.060176345938323356 0.08284966560088404 0.09829568512739882 0.10370556885076737 0.09874917379950518 0.08350953597607076 0.055355592108074704 0.013108178269937295 -0.03996607721382118 -0.09858529849214619 -0.15633627935168606 -0.20679426243712573 -0.2474157118233349 -0.2792542020597825 -0.30407095895643366 -0.3248548580530691 -0.3452618276254781 -0.367108682812653 -0.38969202146221854 -0.41132957931775127 -0.43104435858803397 -0.44905743050649594 -0.46544354878174293 -0.4783393109497952 -0.4840203662373184 -0.47973447701157346 -0.46564480838960887 -0.44338066422446964 -0.4144394171897582 -0.3794046571573794 -0.3376697639274105 -0.28888576858690007 -0.23569268456115253 -0.1829968217242212 -0.13451491223996598 -0.09130786598400292 -0.0539863361285237 -0.025680596829924584 -0.009931621882180122 -0.005594657059190657 -0.007217007423775382 -0.009088166710189896 -0.007597948192065441 -0.0032184132312600942 0.0005295885595437582 0.0016786411438374483 0.0011124468868017462; 0.017262355161718857 0.032875118739464505 0.04623025435494817 0.05612477767629532 0.06054028537871604 0.05877070723272341 0.05087444715873544 0.036369508319271666 0.015167278364857912 -0.011653622904380613 -0.042175653030629125 -0.07323181714758252 -0.10094671860529847 -0.12323247018191466 -0.14036433123153355 -0.15316677838505355 -0.16310320970449307 -0.17254140237967516 -0.18327567354865454 -0.195378154261045 -0.20757129749938963 -0.2187597785636212 -0.22883478410142702 -0.23792563716530069 -0.24505367297865113 -0.24823411205155668 -0.24616964413512496 -0.23913616335374543 -0.2280042470368561 -0.21363568892080742 -0.19659853892934026 -0.1766225066402925 -0.15299818628372658 -0.12667841676050628 -0.10030268347874532 -0.07596858751392885 -0.054002600404003544 -0.03446301687217896 -0.01922830151577826 -0.01048328877251538 -0.007790956175873022 -0.00844025967598499 -0.00933449220837003 -0.00821578445451553 -0.005249699839086967 -0.002482544256361462 -0.001062793980924478 -0.0004516377590053124], hyperparams = 95.6458523223912), (params = [0.007279414516608228 0.010551482504638247 0.008579049658241177 0.0013355714886213528 -0.01100101941924366 -0.02749839484865126 -0.04784111683114872 -0.07222346013855345 -0.0990857935730954 -0.12586374805728498 -0.15017172674574442 -0.16948184481409637 -0.18281762052800196 -0.19101358198030852 -0.19607460794281106 -0.20096654715552612 -0.20779492376216904 -0.21759145956839118 -0.229673726866963 -0.24001580956583726 -0.24467373763623038 -0.24233414734178985 -0.23368944288757254 -0.2212430230839096 -0.2086222076077434 -0.1982233504109826 -0.19036367273717542 -0.18401354985982998 -0.17598071018873226 -0.16311251866231025 -0.14573531465609954 -0.1268532492093506 -0.10885708128098437 -0.09223483121772458 -0.07752180778530936 -0.0671829050406794 -0.06419118815100455 -0.06846062810616416 -0.0764855745854308 -0.08487197134148547 -0.0921329049444279 -0.09822947022896533 -0.10371843292567662 -0.1075676920534544 -0.10599001017655275 -0.09447857743727585 -0.07105235621764437 -0.037951471967316394; 0.01576046073618965 0.025345297465624358 0.025680779452170573 0.01426773795934628 -0.010326566233278095 -0.04632092155799066 -0.09105900437883842 -0.1415378909363332 -0.19321039477672777 -0.24205423709185908 -0.28571335952348204 -0.32229237830530116 -0.35009934208387744 -0.3686907520719008 -0.3815846322702772 -0.3950746614473373 -0.4134801818615664 -0.4383994829880242 -0.4667258218839572 -0.4898450973103569 -0.5001003209332119 -0.4953258577513529 -0.4773467921722661 -0.45098197906508386 -0.42328456685326515 -0.3987805911723369 -0.3784819066939549 -0.3607648921608035 -0.3408454876121129 -0.31385521544630446 -0.2803615851598911 -0.24498897984964926 -0.21189282653449631 -0.18247750437565585 -0.15695329017029852 -0.13762174880842773 -0.12853928606371728 -0.13108602820020446 -0.1418857725658651 -0.1563417371241633 -0.1712490015450831 -0.18473794380806852 -0.1959999296696074 -0.20257430423979544 -0.1980500577175008 -0.17506011777600428 -0.13082832208692122 -0.06967627931050242; 0.02754238609139368 0.04746318071898408 0.05407863683867781 0.04141568231095983 0.0059937678985881844 -0.04965378367794063 -0.11954826563508625 -0.19585696937908562 -0.270522378219461 -0.3388348890413045 -0.3994496278093461 -0.451447913783275 -0.4925038322969914 -0.5223090539690619 -0.5474117450524455 -0.5770726246501239 -0.6161734332143433 -0.6637814867841308 -0.7120935021522624 -0.7483708485557968 -0.762773564820941 -0.7539331506406171 -0.7254603319080335 -0.6842886249874374 -0.639408592104436 -0.596610470355423 -0.557454672812599 -0.5207284935352162 -0.4822975957043896 -0.43837258440616755 -0.39017071871379294 -0.34240522912447924 -0.29919426112974123 -0.2629211262525165 -0.23325354348553168 -0.21005458244806652 -0.1957967273450474 -0.19259540216799348 -0.19936151127546994 -0.21297431398937108 -0.23070859222283316 -0.2500687500358799 -0.26728363958837315 -0.2758654078186644 -0.26698447037799566 -0.23311687367056633 -0.17269112925485497 -0.09160709659736065; 0.043227066089402126 0.07679541874646993 0.09174342006997195 0.07957168704617681 0.036388835659091 -0.03449317022561987 -0.12482137535654617 -0.22327135589718833 -0.31963361168172716 -0.4085972078363972 -0.4873850152736737 -0.5535521591245144 -0.6067262339354665 -0.651672961089468 -0.6981514381409437 -0.7547326493494141 -0.8223404755407787 -0.8940925685830603 -0.9584059489747405 -1.0016096531941354 -1.0151220991514438 -1.0000837337355626 -0.9623499962138629 -0.909970218409264 -0.8513015716588832 -0.7911394574959891 -0.7303726738395274 -0.6686426595218093 -0.6043817859293007 -0.5378266065862393 -0.4725966764339215 -0.41329938001512057 -0.36267743418009885 -0.322981314982973 -0.2944341155491393 -0.27473193312295874 -0.2629708700523488 -0.2583331187223633 -0.25948729822387223 -0.2655402028208873 -0.277090397702021 -0.2951130470521729 -0.3149605700270558 -0.3245925269181256 -0.3113861992024307 -0.26873844371313094 -0.19743104445966717 -0.10437356177350472; 0.06019830428707712 0.10869656032819232 0.1331850048769516 0.12356286056766248 0.07655792731182012 -0.004011075647593341 -0.10854599539799184 -0.22375827824556926 -0.33919828679874675 -0.4486438642418129 -0.5456209786604259 -0.6270055632628487 -0.6987434642353826 -0.7711120750946834 -0.8513184500910649 -0.9406756941573672 -1.0327643076131334 -1.1168762423743843 -1.183324227200774 -1.2230685726151869 -1.231749622588448 -1.2129901426977747 -1.174243601630266 -1.1225987970658327 -1.0631128418225193 -0.9961501228401768 -0.9200484835432674 -0.8341949776861176 -0.7402874321889013 -0.6437172579250485 -0.5529991897480571 -0.47454554376028824 -0.4111464475912724 -0.36395148474046407 -0.3344669583559029 -0.32070685951588196 -0.3184209712604408 -0.3214169443947396 -0.3235135064292013 -0.32330753299312176 -0.324221661539021 -0.3320617119107919 -0.3459278194981688 -0.3523583756897912 -0.3350775625428965 -0.28670551348333867 -0.209291531378948 -0.11032055220774517; 0.07559444751785674 0.13826462898264627 0.17289509106008008 0.1678141647535028 0.12014690550847965 0.03431407861947877 -0.07892125731855981 -0.20548632008930684 -0.335583227361403 -0.4621250545289139 -0.5769487927535196 -0.6802569815976198 -0.7840863682601027 -0.8969087560334673 -1.0148757360684304 -1.128618774768626 -1.2273935969074745 -1.3031989719415045 -1.354659379582798 -1.3821249068728283 -1.3863955262245737 -1.372625209849702 -1.3477786106561338 -1.3159876773668668 -1.2764130080371348 -1.2224941767198347 -1.1475576756456123 -1.0487832377327355 -0.9297787126604996 -0.8001465748529641 -0.6739279150628145 -0.5624776609423913 -0.47208597151122855 -0.4051220141350384 -0.3641817235126848 -0.34967472064262567 -0.35524143127649743 -0.36981521082551944 -0.38113706918967216 -0.3829986133002652 -0.3775944043788554 -0.3725110876813336 -0.3722637616801856 -0.36854399695991963 -0.34537960195880524 -0.29306617213324687 -0.21253730900392112 -0.11148564747237556; 0.08951276350744551 0.16492062444296118 0.20867026113402742 0.20806940681775943 0.1614541271723232 0.07441987560196485 -0.04227782301809864 -0.17551240993967385 -0.31643964342372305 -0.45839963999617434 -0.5952980587929876 -0.7316215929993404 -0.8789641786503966 -1.0345015315311041 -1.1797908737792875 -1.2991255991767572 -1.3834885453471262 -1.4314140154205346 -1.4527074466241277 -1.4596768166190142 -1.460036605407422 -1.459905489681899 -1.46358373696598 -1.470437149649441 -1.4721538607908164 -1.4548207586304174 -1.4044164875781682 -1.3135924286906364 -1.1848227396322273 -1.0297484559488195 -0.8657659802155242 -0.7106624653026689 -0.5772839387920475 -0.4738382106358736 -0.4059527004188185 -0.3770662378477945 -0.3807085164658563 -0.4018804893852553 -0.42417670004156155 -0.43557245017129237 -0.4326807611534665 -0.4200954291838236 -0.4047577651999499 -0.3861372637330806 -0.3537139676402354 -0.2967679041388411 -0.2135972082073573 -0.11134596238693613; 0.10294249056460968 0.18957345199368833 0.2404503126559972 0.24345461186568135 0.199599011657102 0.11549425889140684 -0.000295378645340025 -0.13744539655599844 -0.28862880260939955 -0.44922598878059417 -0.6169566481384297 -0.7970795308237445 -0.9914458420624285 -1.1801258197514897 -1.3351127746525866 -1.44219890098342 -1.4962239239996649 -1.5017297379981485 -1.4800618753528847 -1.4578578973150513 -1.4524084805992872 -1.47030467446418 -1.5107650376204371 -1.5662429646203482 -1.6221015539841566 -1.6587326086359573 -1.6550133512659388 -1.5965445679357928 -1.481346934529784 -1.3198574218383035 -1.1297929568093636 -0.9330425016706583 -0.7496694844406983 -0.5963572485671915 -0.48570582795688344 -0.4255586378878923 -0.41218444150708544 -0.4289159870504006 -0.4561115936992948 -0.4778212079565376 -0.4843667909881887 -0.4732036603007206 -0.4483030694885056 -0.41472888221919796 -0.3703496259913204 -0.3067637718983051 -0.2197060982818436 -0.11427964591576308; 0.11548824980731547 0.21234587788444634 0.2701031907028381 0.2781077016257307 0.23986787674837395 0.1617278333402159 0.048913234637297374 -0.09156021138467912 -0.25504329629618827 -0.44109134002463224 -0.6506820329978821 -0.8826039766045127 -1.1202222926960248 -1.3278374109434636 -1.4769380259341731 -1.5587844296646223 -1.5713330986393632 -1.5252393732701834 -1.4551117502039772 -1.402143316735075 -1.391371283319658 -1.4278954012100202 -1.50360791702822 -1.6036894361546263 -1.7100425766613012 -1.8018141726604833 -1.8541789686444543 -1.846172499026385 -1.7688449605774184 -1.627321445632191 -1.4356456830803948 -1.215500584387008 -0.9910130162938432 -0.7867660466054273 -0.6245852896409454 -0.5188852326077295 -0.4714589188796244 -0.46869487457137826 -0.4894005364228368 -0.5143866893702937 -0.5301332864467335 -0.5268684943282185 -0.5006195097209792 -0.45648854251944165 -0.39993988432345867 -0.327833608433876 -0.2347717408048235 -0.1226463168496043; 0.12689374517986923 0.23361301185557568 0.29974768984404815 0.3161395652122169 0.2867745173856929 0.2162290012769477 0.1069922426095009 -0.037402204733738995 -0.21774979763641364 -0.4392991030827511 -0.7017000621709815 -0.9885225672415988 -1.2613634823511466 -1.4749745879139724 -1.6057743328133314 -1.650990624541621 -1.6141205860665127 -1.5166681360367777 -1.407104929026135 -1.3344188887766306 -1.3233645423597298 -1.3738461617466349 -1.4718588573979348 -1.597780250038176 -1.733783306184653 -1.8628296089406158 -1.9618527213167027 -2.0082479830123647 -1.9866083255307174 -1.8928971758486535 -1.7319639605299142 -1.5197744294054332 -1.2791051259073776 -1.0378077384288762 -0.8269461814625987 -0.6695090003055999 -0.5750319252223569 -0.5372349654890848 -0.5374082865021138 -0.5541544107912387 -0.5717330693745103 -0.5766292554376088 -0.5562111685847467 -0.509188209734131 -0.44347232695041694 -0.36150232120404807 -0.25914598668676153 -0.13606112128574105; 0.13714196184793925 0.2528935605538267 0.32821149347851525 0.35541540256721516 0.33694883184043545 0.2750138220517946 0.16992557231802416 0.01975447777919742 -0.18425039086081502 -0.4507287862142407 -0.771287773124286 -1.1101395532615523 -1.4101510487208533 -1.621492611553205 -1.725869254865797 -1.7272077994500623 -1.6410690992168402 -1.505306116803158 -1.3772707404339195 -1.3021760703547243 -1.294893493896111 -1.349104598050125 -1.448254527317827 -1.5713059131042522 -1.7051467163530274 -1.8396714216797576 -1.9603657194531754 -2.049068295536288 -2.088793469926382 -2.064367061613973 -1.9669820741391844 -1.7998610106952972 -1.5787378969051904 -1.327369955864301 -1.0816566623986759 -0.8749170522007259 -0.7268489464149748 -0.6421124342256782 -0.6088014728517666 -0.6058389148269032 -0.6159025469731391 -0.6241415202226319 -0.6120050028062655 -0.5687292016481976 -0.4981582056950935 -0.40563044419022404 -0.2903827348367224 -0.15256283124054426; 0.14544857644713108 0.2682568713593173 0.3514457959653432 0.38898654217314643 0.38157410142212106 0.3290940205481874 0.22841027178094198 0.0698075851119161 -0.16261424466541832 -0.47627462506903256 -0.851680127182186 -1.2364609714596284 -1.5601894163959398 -1.7694470334380434 -1.8483895746656613 -1.8087583287536193 -1.683219850195988 -1.526929658344872 -1.3997588913223131 -1.334218382142611 -1.3314770943089493 -1.3789512849043786 -1.456188975894787 -1.5444629865758535 -1.6391459425300614 -1.7412855328255528 -1.850921672455836 -1.9600382530936493 -2.054813991577096 -2.1105202385131325 -2.1021970932654686 -2.014506986310325 -1.8500297382477997 -1.62336258144586 -1.3670088175011168 -1.1226390296492677 -0.9221399772868974 -0.7836113725882364 -0.707005101633663 -0.675217309438376 -0.6697290545683369 -0.6746196519579936 -0.6676898346233253 -0.6295574522622375 -0.5566557003927045 -0.4537608296090468 -0.32376343729636736 -0.16955882574133319; 0.1502216999457052 0.2765739950320156 0.3643562389875444 0.40949634202968666 0.4113429636951138 0.36700836656117825 0.26840709340183905 0.0985311585405707 -0.1619267689760956 -0.5161734547527312 -0.9363696389254165 -1.3600053021434229 -1.7070442059158655 -1.918846103774835 -1.9800492701737642 -1.9105916699458159 -1.7598000126223778 -1.5967051699340638 -1.4795756856421172 -1.4286062106946862 -1.431664158557183 -1.4627851747617058 -1.4943004237060382 -1.5141229539824752 -1.5308355231507842 -1.5632898221221374 -1.6305929859921355 -1.7393496788996679 -1.8801865064174013 -2.020470743518029 -2.1181176733883507 -2.1355670618337355 -2.05746048570708 -1.888212128047311 -1.6520491682965854 -1.3917989748546473 -1.15010770536485 -0.9589083152946737 -0.8331555363108161 -0.765504158824181 -0.7379878556967086 -0.7324844426292038 -0.7243135419384347 -0.6877977332690812 -0.6119839125243302 -0.49919966550315015 -0.35483773211044417 -0.18501490143420307; 0.14991942579027154 0.27499031810914054 0.36226615598747725 0.4092183410291541 0.414196582813631 0.37177087425852423 0.2698515527336289 0.08769285594130914 -0.19375554401286668 -0.5746973004233072 -1.0249794812770139 -1.4767298394150663 -1.84208181354408 -2.059147500443257 -2.1143948520791556 -2.0336266901010958 -1.8766930882956134 -1.7194513205705662 -1.6180396663792056 -1.583340111324714 -1.5865035405088386 -1.5834793085809444 -1.5415741047629157 -1.4588237294171886 -1.3616777026306506 -1.2928150683105555 -1.2949269680239477 -1.3912215146315683 -1.5753317285572581 -1.8039453206067375 -2.0168427275404697 -2.154261392864251 -2.180851402991313 -2.0918803529732655 -1.9041695375604015 -1.6559832761632798 -1.3942900908960068 -1.1619676601445477 -0.988579520841854 -0.88029601367554 -0.824423828122845 -0.8014246237540209 -0.7843670049769953 -0.7434607639259055 -0.6616904995435439 -0.5384711434570882 -0.3808513735770388 -0.19762613631500184; 0.14406928502503563 0.2618081159869725 0.3406312411388748 0.37928189826471254 0.37656621308634347 0.3266420735792169 0.2166939657689447 0.026326868834317625 -0.26192995012761033 -0.6490745051029518 -1.1075564110681093 -1.568164949609399 -1.9415815494870816 -2.169765521973778 -2.240954013471999 -2.179546662100219 -2.045644549984254 -1.913412591926024 -1.8330102355734168 -1.8038079342674447 -1.7828497647703672 -1.71687696933641 -1.5744156314141269 -1.3624604169888461 -1.126008105103365 -0.9358103531890523 -0.8613704060187 -0.9438103317267105 -1.17419853204385 -1.4939787988677855 -1.8220642930051816 -2.081077136152666 -2.2191357776322547 -2.2223250579389457 -2.101436307702288 -1.8891067759669036 -1.6320483158558379 -1.3782879396784606 -1.1679655453192532 -1.0203987689370264 -0.9312850164120254 -0.8834072027268793 -0.8496779358125227 -0.7977167275704726 -0.7057806891045232 -0.5706467582715836 -0.4006576384507056 -0.20668863598023232; 0.132430024391535 0.23576620722087532 0.29637133243418484 0.31445307301362646 0.2914390443758141 0.22398907334613133 0.10247291466869217 -0.08887804043920186 -0.36469553400621757 -0.7295122146068846 -1.1628257721681472 -1.6029928623489815 -1.9726040834796057 -2.2238328073602798 -2.341490857961106 -2.33906808500215 -2.266563583981556 -2.1843351036273937 -2.125901930195044 -2.080083989573912 -2.0016790774327333 -1.8418616773796364 -1.5747051224963118 -1.214577416428628 -0.82570744570404 -0.5070791563441623 -0.35703137026449755 -0.43385072381720524 -0.7160979167206839 -1.1258456346715362 -1.5637294641964141 -1.9381895587709002 -2.18580696278159 -2.2844127365845464 -2.239137900333125 -2.077152504518098 -1.8433320710804024 -1.5873458001859269 -1.3545948967268404 -1.1747816221699328 -1.0529389843468906 -0.9761197391727963 -0.9195938721389527 -0.8509777700808165 -0.7452305823700707 -0.5969055262247539 -0.41543039727304737 -0.21297070585630234; 0.11545868860090895 0.19816936316093514 0.23243803207800048 0.2195294068958375 0.16434953746240538 0.06838694174300858 -0.0701084868255921 -0.2565390599701158 -0.4999760517475512 -0.8099514504518563 -1.1787330063631778 -1.5643909359287 -1.9149938124979125 -2.19628463613515 -2.38418641916294 -2.4750576069630466 -2.4999819653876183 -2.4926148620671476 -2.461984971450207 -2.387801999051271 -2.2301577067142406 -1.9535645843728873 -1.5423209228230206 -1.0241048979952494 -0.4804079551844047 -0.034865174682986104 0.1809824649331646 0.09810563442407698 -0.2419882113161446 -0.7346511654656411 -1.2706138333588466 -1.7506463627261375 -2.1001863016868234 -2.289705288732265 -2.3206945686489395 -2.216079855329806 -2.0175384439567585 -1.7732878051120458 -1.5306314186128172 -1.3271670093208183 -1.17725915484989 -1.0730195100408288 -0.9922661187180942 -0.9040483395807085 -0.7823815525099057 -0.6205467631342971 -0.42838115677304783 -0.21843055099997746; 0.09496080937022253 0.15446496885289432 0.16005755200308971 0.11196194761481783 0.01706281647289004 -0.11690921136735613 -0.27921879870555133 -0.45965551830576934 -0.6587441252627235 -0.8901780024980164 -1.1623372623592263 -1.4626890487147437 -1.7729690112697118 -2.0739898859029995 -2.3341828026353095 -2.534013531637926 -2.6790187582935934 -2.766952656148501 -2.779367776567513 -2.685468725921095 -2.451369400643058 -2.057365102767867 -1.50422597727545 -0.8381249538816166 -0.15347475554271775 0.4015995774966862 0.6658112344923455 0.5699924643108948 0.1741375875932973 -0.38626912947806635 -0.9950164208234533 -1.5564015657123726 -1.9892713457549032 -2.255745955957408 -2.3544563960871807 -2.3059536407529246 -2.1481813437890755 -1.9249043500376541 -1.6819527439775144 -1.4633488302825164 -1.2925081396647176 -1.165989414127373 -1.0634634707608661 -0.9558161403333306 -0.8178372986590742 -0.6428091446955878 -0.4407120819259999 -0.22378533444139706; 0.07306355785091138 0.11099981438161227 0.09257591928160651 0.013935548162900383 -0.11925525498799162 -0.29351359825175427 -0.48375496566202836 -0.6624116976559208 -0.8196564608922708 -0.9696432952588061 -1.1340952630484367 -1.3305493113105222 -1.5754219334707424 -1.8681895033228724 -2.1793130512308148 -2.4784829825258257 -2.74010849677186 -2.925230797624728 -2.9924085156160656 -2.899667215638932 -2.616561381934929 -2.1370112506685857 -1.4807969711595448 -0.7130535027123377 0.059087757455437276 0.672272916351622 0.9559520885592825 0.8523902701598294 0.42810147935544884 -0.16420657095348112 -0.8036959288262095 -1.4027862541558336 -1.883189491896076 -2.201902158392876 -2.3520945930926764 -2.3508452929034394 -2.2320545993124097 -2.0335460532148444 -1.7972502942297945 -1.5707853170492634 -1.3857279386269516 -1.2432843764426684 -1.1238401556146216 -0.9994361010664172 -0.8466618725207089 -0.659872574750666 -0.44947132365442566 -0.22731257946748717; 0.05067543637941472 0.070994936146034 0.03817506080595195 -0.05808577433066605 -0.21694825903121873 -0.4225615465565477 -0.6390254249887032 -0.8245672854135979 -0.9574233743762108 -1.0455155112823358 -1.1157320792754748 -1.207349864163052 -1.3663856621643253 -1.6161470456959022 -1.9398092539559872 -2.3003900921810083 -2.6438101911982432 -2.904384946118834 -3.023308939563443 -2.950231651654398 -2.6587490837817636 -2.1521525877398853 -1.4728130905112526 -0.7022218400136376 0.047462146967070316 0.6281548319314597 0.8935984804501023 0.8005369064887227 0.4074140971437206 -0.14713164772046264 -0.7510491911419538 -1.3262073647204824 -1.8027881783316408 -2.138458531957123 -2.3187709602929676 -2.3522096307190186 -2.2666519424020946 -2.093493965102792 -1.8688013509749226 -1.6407550454820354 -1.4469858550578765 -1.2936692323751577 -1.162672630930289 -1.0262957527452694 -0.8622379756749916 -0.6665680676949912 -0.4509024520517794 -0.22698739355605363; 0.0275775923203267 0.0339194327557979 -0.0027941126665145593 -0.09971515407570936 -0.2640657800397227 -0.4833946098583219 -0.7185051153440304 -0.919189694728062 -1.0509817711443696 -1.109192076417005 -1.1160253145474566 -1.1198527938470955 -1.1872320706012722 -1.3661628880373282 -1.6583275515690519 -2.026646142012306 -2.399379615793388 -2.694479920020672 -2.8409049177977233 -2.7881507990725547 -2.51884781802942 -2.0501854264596604 -1.4493488911049173 -0.8001030644218313 -0.20233836285987553 0.23800074531749385 0.4334190701057233 0.36379234288602164 0.0659814969646263 -0.3707005975099768 -0.861147595933643 -1.3398927700439904 -1.752641613427466 -2.0641549568288697 -2.250778279901817 -2.3066853876833995 -2.2488040592132963 -2.100618476000928 -1.892097707275962 -1.6691661529058779 -1.4725506208909696 -1.3132312454923052 -1.1754026950606136 -1.0318096136414026 -0.8610905813860363 -0.6609096430479022 -0.44413194759978597 -0.2225519236521291; 0.00217720217792809 -0.004946151342560594 -0.03925543534454304 -0.1230294736079732 -0.2731972652579516 -0.48652292217443754 -0.7283342286150947 -0.9457450342775463 -1.0937029498201947 -1.1528209516017869 -1.1338125676123447 -1.0817778413314405 -1.0705025988686292 -1.1669366102622096 -1.393131709577334 -1.7169612810504045 -2.0593045267021037 -2.3326513513975886 -2.4627512162734093 -2.4052825341778084 -2.1575627854448927 -1.768108731451622 -1.3260363740255035 -0.8949148262874193 -0.5304450717166667 -0.29326164476396516 -0.22134538058899264 -0.3001429440546772 -0.4961080621479225 -0.7744014350359997 -1.096556432284815 -1.4222492594562508 -1.721279825308266 -1.9718598003943755 -2.142176061912694 -2.2094145162659484 -2.1755215016640337 -2.0529641695873 -1.8649116823019214 -1.654411778375531 -1.462533267170287 -1.3029767553603053 -1.1626102218466707 -1.0157957800943007 -0.8429752801297341 -0.6434714996101101 -0.43049372946707787 -0.21512464298702869; -0.02657198953920521 -0.050681367755038224 -0.08446596362968406 -0.15210495398772422 -0.2783647917142491 -0.4711844488394114 -0.7055571672552724 -0.9314148391608639 -1.0988487751899323 -1.1775481888442436 -1.1648307253286871 -1.093176463440693 -1.030027685462403 -1.0506554557735486 -1.1944657626043742 -1.4366019142593602 -1.6978056921259461 -1.8942639968646167 -1.9573126706745592 -1.8493448134546748 -1.5904755542623383 -1.2794184465379608 -1.0257700899405824 -0.848911218196474 -0.7462501531941352 -0.7342136127383384 -0.817191000112094 -0.9486216985615045 -1.0846029692560246 -1.2217103018664233 -1.3665156105033807 -1.5161883356974974 -1.6774455881603114 -1.8467290229729811 -1.9856135172946616 -2.0566328039685864 -2.045564313763454 -1.9509483533845846 -1.7888107964408064 -1.5985392885605372 -1.4194436967715927 -1.26632877239839 -1.1281839963852585 -0.9820782105261702 -0.8117410716525807 -0.6180042162333664 -0.413013810541572 -0.20635587552832127; -0.05734665077129361 -0.10394854252698629 -0.14642990076010035 -0.20743494434773416 -0.3142762028463892 -0.4826410820342969 -0.6984880952114118 -0.9193992418212763 -1.0968717504948795 -1.1957466334622584 -1.203588323497339 -1.1385961692055189 -1.052497580606794 -1.0166356450682927 -1.081211269032466 -1.2283438100051358 -1.3827103908961915 -1.4695079010817549 -1.4299912116887867 -1.235648940422018 -0.9302299808768256 -0.6613482369249435 -0.5678557792557803 -0.6262906634852237 -0.7708781885855255 -0.9731450226438818 -1.2110874300565417 -1.42015500229485 -1.544500804931077 -1.5880480433769442 -1.582771816156181 -1.5680959404554675 -1.595208712734609 -1.678813303200242 -1.7778735661955993 -1.846918486257884 -1.8585017943342326 -1.7961356810528577 -1.6669697921917142 -1.505935770964325 -1.3487175171025407 -1.2093933033014757 -1.0792748776818242 -0.9388965594934433 -0.7753682822117104 -0.590745080197934 -0.39564101102923455 -0.19805147262921471; -0.08856111013522146 -0.1633321985939394 -0.2272798264735861 -0.29875629756085703 -0.4013461914583095 -0.552402737635331 -0.7469205664234239 -0.9524710295985769 -1.125463351354555 -1.2302685344232345 -1.2510952402677757 -1.1986116015336035 -1.1091907651677853 -1.0402215856208048 -1.041694591132244 -1.1023748304261383 -1.153933128455293 -1.1318200966281242 -0.9914405506532227 -0.7149928110868058 -0.3578372735044735 -0.09705695905547711 -0.09893511134453742 -0.3245177145188128 -0.6511520034822533 -1.0146690793301427 -1.3748161001623638 -1.6562817844985664 -1.797267072274561 -1.7987722772036183 -1.6976872427869922 -1.5625908906358932 -1.4795687074536523 -1.4799610169958377 -1.5312750766061198 -1.5913681276550977 -1.622992292233212 -1.5948491663772775 -1.5050941769476018 -1.3819008808226887 -1.2550694054850478 -1.1374501726813788 -1.022226942596446 -0.8929707242422295 -0.7399697074887654 -0.5661685269291062 -0.38079836514633475 -0.19112852165980088; -0.12072322331712218 -0.22897748855738376 -0.32638690029191514 -0.4256992277463845 -0.5425295675088033 -0.690400940966004 -0.8693962268583945 -1.0563048348092783 -1.2127814722674066 -1.3044189983415044 -1.31864648522444 -1.2688186492723965 -1.181847468270745 -1.0956036178553226 -1.050885818234254 -1.0429697596645349 -1.0135968575203504 -0.9094041594800422 -0.7022336972319522 -0.38731873393951705 -0.015622433574000021 0.24438829065333678 0.2178489467112414 -0.06970565119836052 -0.47423934664070794 -0.9136624974780986 -1.335098374115707 -1.6599145952961418 -1.8270280060090602 -1.8322118491519406 -1.7020598477726885 -1.507986879125811 -1.3491698132698564 -1.2737090797205854 -1.2714478762068 -1.3127820423369567 -1.3560120339930626 -1.3599941646181892 -1.3137308385852073 -1.235101882228747 -1.1454988100190624 -1.055533901169824 -0.9605989804814034 -0.8472627967415969 -0.707906575655623 -0.5458679514588353 -0.36959587262898924 -0.18629243464605266; -0.1548616759004495 -0.30044500633709803 -0.43866364691513565 -0.5771644198997901 -0.7225442236793824 -0.8813430292772211 -1.054147222495913 -1.2241803379286673 -1.3581229428324653 -1.4237608618084725 -1.414724413094179 -1.3527604494101735 -1.2619698011081626 -1.162025275475454 -1.080158293465674 -1.0185319343788928 -0.9326126013174735 -0.7806368696687519 -0.5507151986943689 -0.2531849197633555 0.07572675540933543 0.3166765202252 0.3183095068008251 0.07455186835914529 -0.2992005246194049 -0.721317661452909 -1.134656620527884 -1.4671912777552516 -1.6627480269822024 -1.705689215387197 -1.6007649154915153 -1.4026218335859515 -1.2047922693165052 -1.070343362335293 -1.0165313802674578 -1.0325817877959689 -1.0799200730972964 -1.1121189449460998 -1.109545632732466 -1.0779168238638301 -1.028721725042726 -0.9700414135619917 -0.8990130042913611 -0.8046599135323147 -0.6810227560002962 -0.5314156353726069 -0.3634318872389831 -0.1843793398287231; -0.18986087876971106 -0.3741052087171557 -0.5547712041282512 -0.7350490706583563 -0.9141906766067572 -1.091866708225018 -1.265598593830296 -1.421239573492332 -1.5311363072200732 -1.567448538527494 -1.5287516456496821 -1.443892964776583 -1.338520820556279 -1.2204108618372846 -1.1035018330320583 -0.9960196378569379 -0.870953952006899 -0.6997984519453456 -0.48278402417191696 -0.24083090298557722 0.002999625362978545 0.19439259469390766 0.2347305858999582 0.09642033904749739 -0.16332025548114368 -0.4857357794654562 -0.8293165883375795 -1.139807866841511 -1.3644760482275347 -1.463005691039741 -1.4110536827032494 -1.2407021790292794 -1.034379806263575 -0.8642142617524506 -0.7713233626849426 -0.7648184779250229 -0.8132777124503587 -0.8702892711506425 -0.9087293279739469 -0.9218850001749962 -0.9127064486960542 -0.886400144898103 -0.8408381845786791 -0.7673829851020058 -0.6608747668629389 -0.5236351831725785 -0.3625171305289042 -0.18538122177819055; -0.22270412761015038 -0.4436321695608286 -0.6640004410005061 -0.8821303303631782 -1.0918218033921077 -1.2880640035213087 -1.4646647794694883 -1.60753132942722 -1.69488192740128 -1.7051664551636248 -1.6384175360682445 -1.5254283013172207 -1.3965307500647004 -1.2557128513864022 -1.1045903270902233 -0.9535399899086611 -0.7949393221349015 -0.6172375474058933 -0.4314389422337945 -0.261441959814873 -0.11919404347313982 -0.006255983217171145 0.04603350617619486 0.01718912757792874 -0.0845883898870629 -0.25118240614750215 -0.4823852507129198 -0.7519710509601361 -1.0010912196968949 -1.1535258825245427 -1.1549771765320784 -1.0222137951734542 -0.8274548021542087 -0.6444604187951936 -0.531993443500024 -0.5138481932287925 -0.5669781799580039 -0.6475074354865548 -0.7214111036247915 -0.7729641532770791 -0.799992045143042 -0.8050549188284704 -0.7856193056294315 -0.7343494896824424 -0.6460971078998388 -0.5213525750870354 -0.3658952249962141 -0.1886407478427701; -0.24965912514467611 -0.5014326263028659 -0.7554483479919412 -1.0047842954456192 -1.2383232787227054 -1.448003190684079 -1.6254115930202768 -1.75663903009714 -1.8252807744668305 -1.815959900964176 -1.7276353213722622 -1.5880710333333397 -1.4320111247889125 -1.266129370347195 -1.0822290826878669 -0.8869102241545861 -0.6901312995933705 -0.5007480515895045 -0.34081283779204935 -0.23523432910008724 -0.18531189179254948 -0.15952464574028694 -0.13332639469982388 -0.10200971114538235 -0.07734971806634941 -0.095820013452067 -0.20640254334935368 -0.4174387172137044 -0.6597460480390143 -0.8279651506746233 -0.8543789030392845 -0.751131139771175 -0.5773145441405273 -0.402900854833902 -0.29365642233716643 -0.27976346570891125 -0.3446557869875327 -0.44679925300023854 -0.5488229916779785 -0.6313557497704746 -0.6900125408253859 -0.7243718411903921 -0.7307033546065272 -0.7029558038321452 -0.6350292017217627 -0.5238672665451517 -0.37338129582532603 -0.19410262934769434; -0.2690528953279944 -0.5434638267924625 -0.8228450195822506 -1.0958840576174445 -1.3466471880228095 -1.5642834298862733 -1.73995305845242 -1.8614773022935245 -1.9166251310678928 -1.8946253965965536 -1.7928005653493564 -1.632948411981453 -1.451295974637442 -1.2606511862488343 -1.048025655808192 -0.8118819812638586 -0.5719769911295884 -0.35621609322489817 -0.19694287290050566 -0.12113043547116882 -0.12540582911357956 -0.16410634519172268 -0.18388050474845039 -0.15632620414349543 -0.09309824922483785 -0.04540161503879427 -0.07974495379006136 -0.2174736315999417 -0.39686312629247666 -0.5208960274284489 -0.5325996674709602 -0.44173967592858565 -0.29145669363363763 -0.14267509228600328 -0.05725339946537988 -0.06283772471404896 -0.14431630101589232 -0.26424361283250253 -0.3878048262497428 -0.49594640631838083 -0.5823256752040767 -0.6436052697896137 -0.6758554023668152 -0.6734425008575105 -0.6275128197189452 -0.530727752380745 -0.38470187712131576 -0.2017117914299837; -0.2838360238428966 -0.5741935707800042 -0.8704381929874753 -1.1591208081565803 -1.4206964016833834 -1.6415628017590083 -1.8136794743163935 -1.927999297828645 -1.9752382501310144 -1.9470912714285518 -1.83950798360943 -1.6666335281219324 -1.4614741602533825 -1.2452345762000692 -1.0098220734278722 -0.7466222690974684 -0.47266243675751146 -0.22397515488376887 -0.03980158531788436 0.05020411416353849 0.04589839827352392 -0.009884719618127742 -0.06007479830220324 -0.0673666345556717 -0.03328660489623351 0.005312586920688812 -0.001680926201410789 -0.07238540796730857 -0.16703739178587407 -0.22097887469774155 -0.19973557146750967 -0.11156076928570755 0.013612443699922771 0.12494370738390854 0.1719043255096742 0.13729339819909 0.037513242795302056 -0.0968759265318428 -0.23761805892306068 -0.3671421209212011 -0.4776634583837224 -0.564793409561435 -0.6239622068980544 -0.6474966462887716 -0.6231097074708346 -0.5399365028645782 -0.39766489786493886 -0.2102091555376654; -0.2975034689055267 -0.6003975111675783 -0.907240282374816 -1.2043800605596862 -1.470888016077357 -1.691065343062652 -1.857926181857438 -1.9662150626091766 -2.009132921191581 -1.979637181823659 -1.8731806701274607 -1.6965120066966894 -1.4739687140927764 -1.2316213199715333 -0.974680651951742 -0.6970948030832516 -0.40756321809363744 -0.13593432892899712 0.08037743905785748 0.21152664417741135 0.24955710305464007 0.2221814295200953 0.17595960248957956 0.14583720696449087 0.14010189427659317 0.14509016092549004 0.13948889491956806 0.11429162986481005 0.08756854464774476 0.09113786769312697 0.13913973442720948 0.22396366950928276 0.3217448218241529 0.3893836997524978 0.391442402866098 0.3236185724578833 0.2039553110996131 0.055345750649160544 -0.10061411029694008 -0.2486308174645061 -0.38127713941856867 -0.4934834772990283 -0.578830748896745 -0.626255950377664 -0.6202906619691813 -0.5483778513215237 -0.40941683595218137 -0.21813519663572553; -0.3098674556643694 -0.6227399511610032 -0.9357470017768226 -1.235995795743866 -1.5035772448980596 -1.7216857038454023 -1.8830037921171205 -1.9851068159170007 -2.024325792403774 -1.995473167324825 -1.8943273324733945 -1.7224782380565389 -1.494267347740988 -1.2335434959435907 -0.9568168906253616 -0.6687916271213447 -0.375551392101643 -0.09613074995326061 0.1410985751600569 0.3116657585441011 0.4042900585350763 0.4301008749172661 0.41752633556978996 0.3940674493132826 0.3745131593447293 0.3632439962890566 0.3590609334188458 0.3605736126158684 0.3736704130976017 0.41071944230424623 0.4735333218377347 0.551623339966369 0.6193974521106395 0.64217074461237 0.6003781143851697 0.4998510369620811 0.35794222511016227 0.1920717893744209 0.01962972751678309 -0.14700844386381742 -0.3006068786855628 -0.435443683827131 -0.5433692661594215 -0.6094718566421077 -0.6164356706552863 -0.5525201270049432 -0.4167993831331151 -0.2236388419153256; -0.31906984398604626 -0.6382569663399383 -0.9530347893430506 -1.2518392726586174 -1.5178804154823062 -1.7348790684013298 -1.89318922485413 -1.990035938103774 -2.024823985128813 -1.9958928134208338 -1.9004418774019982 -1.7373209372971656 -1.5136842695334811 -1.2482741024673747 -0.9616109425380733 -0.6678334531161927 -0.3772824019239719 -0.10244938154275647 0.1389844558290491 0.3312864678387502 0.46574375311440663 0.544142276166009 0.5790020904880872 0.5877922959290734 0.5864452978571573 0.5873953105541879 0.5987055368578036 0.6231617992707069 0.6631370533873256 0.7217313907154468 0.7930831713208047 0.8596166728308857 0.8947035569599756 0.8759768171059713 0.7970409254544045 0.6672173922645893 0.5011708254165776 0.31468937700521765 0.12250622148438745 -0.06437434411302564 -0.23777852676232927 -0.3916666260513632 -0.5159818245218734 -0.5935993686067629 -0.6076493392636367 -0.5482344295606714 -0.4156368831361434 -0.22393244628329664; -0.32404439247449324 -0.6449658923158061 -0.9568027609933409 -1.2498609508678373 -1.511615740554252 -1.727966002659549 -1.8864223444496493 -1.9806879310771766 -2.0113090547915733 -1.9807894634349212 -1.8890703575244452 -1.7348254390655147 -1.521689226010852 -1.263835679768412 -0.9812121126065411 -0.6917482062921322 -0.41084354497379166 -0.15028556537591822 0.08081569028155797 0.2760580766987358 0.4323674795243411 0.5487522645515355 0.6291178883139319 0.6826453816480187 0.7220560254928938 0.759325417059232 0.8042763570345701 0.8607281737783128 0.9292353350924931 1.0065525081480036 1.0809615640533303 1.1308845417161664 1.1354607511814003 1.0844413756465976 0.9780867625595673 0.8238189759362649 0.6345618920682572 0.4258489701497256 0.21155539455230782 0.004048549423741131 -0.18738177702049078 -0.35570989769114636 -0.48983780761790385 -0.5734301383591283 -0.5906090278034871 -0.5331114647354073 -0.40398485867291917 -0.21784066284305229; -0.32308995905700777 -0.6402646928438182 -0.9447297996901595 -1.2288780972229956 -1.4840632161976346 -1.6986374891583187 -1.8582988730595202 -1.9524936113441174 -1.9804846163660432 -1.9479553536898486 -1.8587167896921624 -1.7134744259372534 -1.5151987791334478 -1.2742371606646923 -1.007638963856175 -0.733577547368243 -0.4694043184301318 -0.2283736451047831 -0.0155495514524946 0.1696586529514523 0.3300361590957793 0.46670889215992284 0.581256498647691 0.6786504778367285 0.7666450349796423 0.8529018515948854 0.9437169781437668 1.040727916437539 1.1403160590605042 1.2341359256451294 1.3082435048724648 1.3444095303250794 1.329808498957435 1.2605729480891414 1.1374533700071197 0.9654643526259635 0.7568142630232572 0.526877083186676 0.29135507740748406 0.06492796727620102 -0.14181296323265385 -0.32018315370418576 -0.4596119315095659 -0.5458772871426099 -0.564125081218247 -0.5081403889505532 -0.3840975852419937 -0.20700360461923623; -0.3135094830896676 -0.6203002455349801 -0.913854970092581 -1.1879268660258109 -1.4355055901116485 -1.6461217109675106 -1.8054201828440388 -1.9009228673088951 -1.9292098184319368 -1.8962715864791924 -1.809927450895449 -1.6747133553360283 -1.4947543560579812 -1.2779393994908173 -1.037430695605861 -0.7894494275062552 -0.5501571707393795 -0.3321798016886494 -0.13955316792360534 0.031237546474500572 0.18625873295133077 0.3303909333010925 0.46682586385805563 0.5994914838972921 0.7317410707440759 0.8659852416273978 1.003121829678611 1.1404562960019458 1.269479472445869 1.3789808081507853 1.4566076025847177 1.489879774742453 1.4706263736156897 1.3961851955274986 1.2662491668871478 1.0847938625459128 0.8626830834681276 0.6157280568783234 0.36291564487539085 0.12126952131879473 -0.09703101231419595 -0.28184833914042295 -0.4231397520676042 -0.508901466943429 -0.5270255648028325 -0.47401421708921226 -0.3576661197621121 -0.19258967241858882; -0.2945846013387076 -0.5842052067914146 -0.8637303930639213 -1.1272140801002453 -1.3665389381062882 -1.5704618952578822 -1.726131554114888 -1.8229476375098623 -1.8557183473672494 -1.827207188158987 -1.7465841513594487 -1.6228199168109205 -1.4625118129324681 -1.2733692712902958 -1.0665363383551232 -0.8551538185975579 -0.6512780024126493 -0.4630907433910386 -0.2925710613127815 -0.1359351594354146 0.013030507423779564 0.16047364637922534 0.3111401271021633 0.46875507176486214 0.6344000323115137 0.8064549936064201 0.9814803341916722 1.1526310387256407 1.3082165838977444 1.4358670906147504 1.5251406575881208 1.566574610922277 1.553286872390097 1.4825989297470665 1.3542238951481467 1.1712471417878765 0.9428789480544681 0.6860055761558634 0.42267674685656814 0.17206144843765378 -0.052301084738729985 -0.2390509888250298 -0.378040358113962 -0.4600774328248894 -0.4775785234227454 -0.42946815852581227 -0.32343689166413137 -0.17367817848828157; -0.26823692931547205 -0.5350746923935055 -0.7971238513365929 -1.0478556243817518 -1.2769406036096742 -1.4716162530017676 -1.6206599544696374 -1.7173216656810362 -1.7573751397098667 -1.7395055857700212 -1.6703737090038537 -1.5614751657702284 -1.4223395719032426 -1.2619914274876582 -1.0917320098952228 -0.92249638547966 -0.7613287311960526 -0.6099798493514498 -0.4658542903429093 -0.3244171719588748 -0.1806836320144209 -0.030267933949563258 0.13021646889560565 0.303536218769111 0.49021274092796224 0.6870852757014391 0.8884696709234025 1.085286222975633 1.2645342659988639 1.4131921482554057 1.5208605166871707 1.577974249982508 1.5772496323162588 1.5160612379959202 1.3946044353074323 1.2155405939438775 0.9876652232543195 0.7289952496604368 0.46337897270597395 0.21193909760208776 -0.010179082305791927 -0.19142219168736052 -0.3230252924880197 -0.3991904295332192 -0.41627099343692303 -0.3744922839418025 -0.28101833927685094 -0.15007465918756663; -0.23758063416024022 -0.47759817466464816 -0.7181305020692493 -0.9518463878813068 -1.1669581525556443 -1.350149469541148 -1.4912065824204825 -1.5859685600434967 -1.6326200965291278 -1.6286224665456384 -1.5771037547429196 -1.4887140064534663 -1.3746422311112276 -1.245243888593649 -1.1119799773901669 -0.9840295239032535 -0.8644956431588378 -0.750196992871248 -0.6342418098821728 -0.5101313666679241 -0.3735665650124344 -0.22266054267506197 -0.057260320344874244 0.12376353410173425 0.3210424607698263 0.5315104403587199 0.7486768691340062 0.9629937928151959 1.1613358149976396 1.330153831937832 1.4577720241670744 1.53304070736031 1.547350158544397 1.4975809804572042 1.3844132352558904 1.2116200231682346 0.9895134351387721 0.7368447600320518 0.47768105872573 0.235065078371512 0.025478381803686726 -0.14170247589215357 -0.2610784443110707 -0.32940533503130465 -0.3452744698754367 -0.3102811821563436 -0.2317024993629399 -0.12302021035465702; -0.20661805672603112 -0.4176811804972791 -0.6323285884108016 -0.8437026635666537 -1.0404276205981708 -1.2095573453294954 -1.3412585824239687 -1.432148599791008 -1.4824184037986214 -1.4912799174450821 -1.460336392804027 -1.397282537320522 -1.3124318388003373 -1.2164607423164753 -1.1198731098436312 -1.029569390121494 -0.9459309740636268 -0.8630940154380018 -0.7720856666203731 -0.6651448850135039 -0.5383676557265508 -0.3917717367661063 -0.22783716462684986 -0.04664849151962006 0.1527859650371098 0.3676284679998541 0.5910952771075395 0.8141352779476656 1.0241031916731886 1.206946394649702 1.3494924160723185 1.4390995974727607 1.4658371326152402 1.425928258603944 1.320783336271209 1.156426021381188 0.9457867736379653 0.7076868455381147 0.4648894013141604 0.24107601127916403 0.05266207013173684 -0.094100653910263 -0.19699302623224968 -0.2544327921752015 -0.26704259656071094 -0.23877300260201278 -0.1772526771397208 -0.0936781481512868; -0.1778023989047795 -0.3596132261281049 -0.5450501475805974 -0.7293014404031078 -0.9031512938126044 -1.0545688017713089 -1.173852430448247 -1.2576084717631746 -1.307383232627528 -1.3253684796133895 -1.313835002851434 -1.2776217055000412 -1.2241819973813457 -1.1624693321486126 -1.1006334973785363 -1.0429568892360248 -0.9884855399216097 -0.9304375387850903 -0.859358810145774 -0.7678274826954707 -0.6528096170820812 -0.5155997354429789 -0.35985907905170944 -0.1860500880073368 0.007271547450230422 0.2172649055634199 0.4371845837263979 0.6588678828364677 0.8703381891821715 1.057008500904104 1.204783028033389 1.300473893896537 1.3337970590989432 1.30118733417833 1.20493261998099 1.0529940158019124 0.8604271226313295 0.645650507165709 0.4290595351785681 0.23246444011799194 0.07078896594379812 -0.051918332066764966 -0.13560201337184458 -0.1802730329861126 -0.18869753587807697 -0.16702903859251822 -0.12287346240693539 -0.06456248608490646; -0.14989730592547215 -0.30223573997977 -0.4568389364328627 -0.6110977114675538 -0.758133289024762 -0.8876461762097555 -0.9909885541189983 -1.0644758735870619 -1.1098242597689199 -1.1318715975021651 -1.1348376054483198 -1.1223178256141053 -1.099054584951523 -1.0703823490412794 -1.0400373307200337 -1.0092526854371202 -0.9770748740962738 -0.9376203686760751 -0.882030268626298 -0.8043571420517764 -0.7028226585423616 -0.5792981350501775 -0.43746706635396987 -0.27783959578055967 -0.09885272314879456 0.09668919507137318 0.3025710592358792 0.511453004697627 0.7120279531734446 0.8898537269005036 1.0311905073531735 1.1234310767542675 1.1571446532500782 1.1298824375557266 1.044741133649296 0.9103426320791829 0.7422789962288878 0.5582562393900288 0.37557886917896877 0.21197521798137522 0.07985114563438674 -0.017913511531682958 -0.08244693260187165 -0.1151294614205421 -0.12030442181046555 -0.10510881308647126 -0.07631237998125295 -0.03970759266349971; -0.12025095084533902 -0.24175733031398228 -0.36473530926710757 -0.48783772070103937 -0.6057315123350065 -0.7105802739790884 -0.796007595147513 -0.858050044655078 -0.8970264777447504 -0.9186951506017152 -0.9293344363989336 -0.9328325939698631 -0.9328574055060473 -0.9314704618521609 -0.9271368579510304 -0.9178621162596854 -0.9028655120523662 -0.8778598637028066 -0.8353231366647761 -0.7711426704870273 -0.6849191929140398 -0.5783962419358729 -0.4547451425508271 -0.3149073951495158 -0.15792024338706942 0.013789432494229667 0.19494987556545368 0.37887612036764917 0.555071746426626 0.7107959612905795 0.8345582592419888 0.9153799604267288 0.9451768224898427 0.9228628422645638 0.8522478568508765 0.7412483005187566 0.603868077420758 0.4559497853426465 0.31126454381201374 0.18288335296960848 0.08039842732279805 0.006300505639173847 -0.040626998392256815 -0.0628957250367032 -0.06610246859047457 -0.05710857621158746 -0.04079905636984499 -0.0208506964502549; -0.0886435446753111 -0.17811286263576165 -0.2691580319859125 -0.3609231782727689 -0.44900135396332846 -0.5281182779464849 -0.5944799154512754 -0.644228690937425 -0.6760676152521137 -0.6949893394845296 -0.7077633699693987 -0.7185371808577674 -0.7307273209998758 -0.745049687545335 -0.7569817785338271 -0.7624924896606367 -0.7606945764725954 -0.7481257719071516 -0.7185263270675196 -0.6692654712562165 -0.6010099050626254 -0.5150488844320459 -0.41407117132699267 -0.2998527506380445 -0.17248614928043607 -0.03368729439713932 0.11264605848200744 0.26065136213121876 0.4011465347216321 0.5244768348756801 0.6227324288596917 0.6873239493385501 0.7114459354036349 0.6949762190808971 0.6420900774653417 0.5590207846606174 0.4564383841818994 0.3468611145577351 0.24061781990939385 0.14693008013321757 0.07279581566546876 0.02043209439624498 -0.011073523531920431 -0.024932802199809655 -0.027125737919711585 -0.02312829898727592 -0.015767285260712458 -0.007464442238529875; -0.05729829339636838 -0.11533899645690407 -0.17510876252246027 -0.2359719559348241 -0.294345539375634 -0.34703198366290583 -0.39238955189023617 -0.42739975516835177 -0.45035443168619754 -0.46497171417287053 -0.47647733108379364 -0.48797293552340154 -0.502036230875354 -0.5191733347573131 -0.5352595516681574 -0.5464858265666322 -0.5519993252076829 -0.5486807198826016 -0.5314916651358571 -0.4987931380949708 -0.4516022250271046 -0.3907748305360254 -0.31842680319798383 -0.23684579788895604 -0.14683700941688818 -0.049217864112600734 0.05380145490037564 0.15772689229112805 0.2554377531702111 0.3406868130665836 0.4090428063990235 0.45460446297740165 0.4720507169041051 0.461637982039308 0.4271446656147565 0.3728386046138389 0.3055034168971221 0.23360603729783624 0.16435138024842466 0.10380738833501028 0.05629238371626541 0.02313993837381771 0.0037469024701141593 -0.004524521540269648 -0.006262983049217299 -0.004956445518651291 -0.0022258173669206203 -0.00014161389158973508; -0.027880528802613 -0.05628074327025297 -0.08587106309035286 -0.1162570674173737 -0.1452732139854186 -0.17136595871705956 -0.19413554118633367 -0.21199296615733373 -0.22394638521912064 -0.2321515091895098 -0.23926564335533843 -0.2466671413633592 -0.2555880198544351 -0.2663459480428819 -0.27684578059444265 -0.28502174631732746 -0.2903760202670205 -0.29090114335905787 -0.28355830062241877 -0.2675383760882179 -0.24352197899577402 -0.21197314813884666 -0.17412226697265176 -0.13159410973932778 -0.08507931819068 -0.034753757282887696 0.018585296285656083 0.07245863587574601 0.1228503173697341 0.16667779028913315 0.20203339856201763 0.22587770622996492 0.23517486458479156 0.23015073088364688 0.2131128876851958 0.186310094234003 0.15297037956086554 0.11735912984045783 0.08334407367458108 0.053927894633230784 0.030929530473562696 0.01473156459167701 0.005096026603037013 0.0008001072847105936 -0.0003492452283138823 7.288259615985393e-5 0.0011547714403939901 0.0013930476764658461], hyperparams = 95.62328136826949), (params = [0.047367791750624645 0.095050987444916 0.13493918675511424 0.15959083521395417 0.1652749874085072 0.15364104062766534 0.12880391757765028 0.09412626670950829 0.055375041586910256 0.018035874620239964 -0.01231772622157964 -0.030682028616474642 -0.03874012442999659 -0.03712739969359494 -0.025294987107138085 -0.004553971728095692 0.024056500784839643 0.05981826087054066 0.08785471132367659 0.11046209039549339 0.1323439108698113 0.15707111302136492 0.18182153201943632 0.1972362180054739 0.19682567371139018 0.17628962357570208 0.145531883955243 0.11695063293266694 0.08955616328750923 0.06311869704140011 0.036107469733223214 0.011081560678062513 -0.011558997632885159 -0.031940383270564136 -0.04072634875261263 -0.03262566264398464 -0.014779871052271826 0.009326238922482523 0.03466874672354205 0.060731838190324926 0.08919492076870779 0.11579262204764487 0.1266616228778356 0.11742156248713716 0.08985704255728875 0.05577483705764081 0.02620271426584808 0.009209135202207962; 0.08544607280267481 0.17373790276161255 0.25183170638660674 0.30187916922410796 0.3137110399668429 0.2904334663042697 0.24705003701983141 0.19060357170471803 0.12226563081329078 0.05298333959221811 -0.002529917202939276 -0.03673496941575852 -0.050159873620280515 -0.045204711340722924 -0.021054996292198775 0.020589245730369764 0.07691869883235926 0.14638210124082676 0.20363262784307914 0.25028400172577314 0.29173243332642407 0.33412710095520104 0.3777916078880683 0.40581531810065435 0.407713169181388 0.37276810143565253 0.3159535393931224 0.25390030745102643 0.19055317957680654 0.129591562772735 0.0699461609653685 0.017036420530530685 -0.029986654699428485 -0.0679293888775512 -0.08393141354573329 -0.0701624455806675 -0.03352004315639093 0.01633122023840148 0.06479157511165691 0.11015601340365147 0.15812167443243774 0.19935297140426098 0.21429896909659288 0.19963186707131367 0.1540286396621408 0.09282651107817264 0.04248777222500173 0.014105429802971458; 0.11751647294944044 0.23864363999877453 0.3473493335487015 0.4185740876406424 0.43732714618556423 0.4092741884176734 0.35689529312820745 0.28980761153307544 0.20744229093053337 0.12403180244421412 0.055209392180732585 0.01022285603222707 -0.007690068878948485 -0.0020730571678541088 0.02930550697867432 0.08742207682882847 0.1672612328388156 0.2644999369043999 0.3494625773174208 0.42090745512759753 0.48290709626228495 0.5414961426335881 0.6001627663019503 0.6356421263196163 0.6327332964640834 0.5819575304139287 0.5021561366630606 0.40721097328962885 0.30472740938348697 0.2027613126479507 0.10493905889613869 0.02081276842963794 -0.049896643885376145 -0.09840335808864324 -0.11445036340074226 -0.09480563471522369 -0.04512759150045972 0.022452711982121218 0.08809328553192823 0.1460435836304279 0.19931041952965298 0.23975219778803933 0.2521910049135126 0.23392897655887807 0.18320535326255544 0.11282382156523175 0.05503442832450269 0.0195933941999451; 0.14054085168615923 0.28606418524782545 0.4198087660207144 0.5128650814540122 0.5447551338904393 0.52698278327689 0.47971646219197894 0.41484435557059524 0.33418697808176406 0.24728120033889203 0.16793004475371012 0.11254530493906491 0.08641709485369659 0.08836014581784364 0.12142477497856137 0.18929398658769703 0.2867837136635554 0.40380263886796686 0.5140704084379417 0.6119352133990562 0.6985495992719502 0.7751985156384829 0.8389705283519011 0.8698171482311782 0.8538273608978156 0.78807078084093 0.6870722981787142 0.5604194936959487 0.418660140568665 0.27348526404400814 0.13687674836740343 0.02199278715229976 -0.06681417587698145 -0.12309188412723489 -0.14267012502927692 -0.12156557940945292 -0.0649627086536182 0.013985356778982171 0.0887079400085232 0.15113821822128165 0.2021925471409434 0.23671274883985263 0.24605070109030536 0.2259090760543733 0.1822041476086873 0.12342687026766513 0.07070458318502881 0.031263443816651956; 0.15489690298954611 0.31844156628123466 0.4727572740891326 0.5892454462223085 0.6439527692367992 0.6483102852115032 0.6163727001001496 0.5623471057189678 0.4908151046465711 0.40591189607770717 0.3189718161402849 0.25235830981912744 0.21337114119053877 0.20944034268671488 0.24257952951471096 0.3142646508995481 0.4191050332573703 0.5486690059266011 0.6857013685744963 0.8148978898943595 0.9272182837034186 1.017534510367502 1.0761076284717037 1.0944911212531847 1.0601840441291348 0.9766507236890037 0.8520920964772577 0.6914730271028449 0.5086068992015601 0.3183710632787892 0.14300741577250795 -0.0005185440248998937 -0.10282802529203162 -0.1655595075668707 -0.18903203928096413 -0.16948770445028385 -0.1114208132495536 -0.026257981883522165 0.05575074373626855 0.12146612785613183 0.1697931321486954 0.19805424924221984 0.2049298118584874 0.18797197170888397 0.15901309361112898 0.12020471920602953 0.07796838152462775 0.03919912853944554; 0.16487957116133636 0.340873597103774 0.5118785615268452 0.6500500160425986 0.7318510853452004 0.7624729066268328 0.7502730052594605 0.708566588907289 0.6446423820047552 0.5653906957617595 0.47965531121232197 0.4069363218777887 0.35746931158380746 0.3462682381366369 0.3752030133821553 0.44853559267766996 0.5593611993053276 0.7014834232768907 0.8630050801641795 1.0192650225503552 1.151140136517712 1.2480750726385605 1.2987530735782946 1.303471759946235 1.2488665952952995 1.1404693922295648 0.9857560264492428 0.7866431615804407 0.5590532712097466 0.3235059564462035 0.11261694156311852 -0.05354592935835877 -0.16651572107231977 -0.23829760344488032 -0.2677218164319478 -0.2531758683980546 -0.19834851856790153 -0.11391620378886283 -0.023830422240676878 0.05074014887990913 0.10238068759319256 0.12764113047209497 0.13480289926970615 0.12832125602911945 0.1163235724730849 0.0960824108482645 0.06744955737684395 0.03493799635029907; 0.17826529739833888 0.36374519242056036 0.5448102386013586 0.69897204395704 0.8010399892546074 0.8491184079032448 0.8509492545090728 0.8167455894506207 0.7579532205691445 0.6881811229815455 0.6098830231580585 0.5373480355334527 0.48631701583571496 0.4748448719525073 0.5052949325560531 0.5820353897418692 0.6986701023284031 0.8525366094504542 1.0324519105712167 1.2082965501026175 1.356341821334183 1.4584738009449922 1.5050042362722684 1.4982480483903056 1.4242151252070554 1.2843776676399652 1.0899139510546492 0.8447308238173076 0.5676857010277861 0.28701091830624226 0.04097380290323795 -0.1490881234832822 -0.2782753573490287 -0.36487375425006097 -0.4063996107542991 -0.40032946961185767 -0.3481838026360223 -0.2647629211345918 -0.16509952421884616 -0.07434474957022315 -0.008560472404744043 0.021988372943668552 0.03503490437365441 0.0462604521895378 0.054367166720733995 0.0505401995170494 0.03801254476128396 0.019271290965777888; 0.19433080253372959 0.3914671294575676 0.5797430859553766 0.7407978944853806 0.8501866143742065 0.9055110747125884 0.9177912223817161 0.8933445098893392 0.8424655383361105 0.7789350064623329 0.7026352093902061 0.6313838025874885 0.5815928264250224 0.571674934210147 0.6086998658798068 0.6950544412933469 0.8231678179615018 0.989707085760694 1.1793686501873564 1.3635207331604122 1.522039189196578 1.6312079055018431 1.6785736591598337 1.6624205850042486 1.5710271190025509 1.4015036621461114 1.1664122865801172 0.8731246757447221 0.5444014625844714 0.22094563353601043 -0.05808280079224662 -0.2757650526302938 -0.43070411077234094 -0.5398958205218186 -0.6000983113948767 -0.6077402689292716 -0.5622307229200239 -0.4775470026625575 -0.367778221883138 -0.26103170001712667 -0.1739838981839837 -0.12338807827042303 -0.0946032074571008 -0.06534342344727313 -0.037412523021105475 -0.020429304263786058 -0.011155738745337996 -0.006903483817580103; 0.21081655094036622 0.42090002893114087 0.612759272933439 0.7710370864690143 0.8809020758795744 0.9401427536289702 0.9598499783107963 0.9447029412446001 0.902411188841071 0.8430918039559295 0.766308253435052 0.693147792192772 0.6380387231897693 0.624209081147618 0.6690343298486828 0.7711589851666032 0.9174138661920999 1.100912698443214 1.2992902484828879 1.486524307012549 1.6465038005172319 1.7557950454501694 1.8013717953407413 1.7779555252469568 1.6742351240092344 1.483136634210065 1.2138981014064585 0.8795679859177697 0.5075740348121713 0.14644507621490602 -0.16487574326158666 -0.4129067500696062 -0.5974597452070256 -0.7305257758292498 -0.8082739948339954 -0.8292752303810385 -0.7941411122034399 -0.7103705238398595 -0.595649675633098 -0.47848553179917747 -0.37264531108865934 -0.29709132651594317 -0.2437131681805774 -0.19352381769709417 -0.14235056814323105 -0.0967790041378087 -0.06246136934688987 -0.03362377244826041; 0.2236822918072351 0.4412379679152373 0.6337096031200234 0.7879336517213772 0.8991657603007677 0.9646329194272625 0.9932711704524485 0.988473392228032 0.953971693348368 0.8970259938363283 0.8173479932089489 0.7355766567886948 0.6680493444527745 0.6448853537134325 0.6942015342073977 0.8089836603936145 0.9711769000368218 1.1719168039961452 1.383570714928947 1.5763682586468861 1.730581107685951 1.8290908879248047 1.8648981026922178 1.832780574774014 1.7200670251330497 1.5152509030456904 1.2246615569254429 0.8647974491419459 0.4682859480979558 0.08470233772085584 -0.2498746876338761 -0.5242874879078179 -0.7368717821108722 -0.8922724517989029 -0.9874316516562726 -1.0242337025815011 -1.0042907720675978 -0.9316624587336486 -0.8225718903608649 -0.7004768416764124 -0.5801685424873099 -0.47964620645463596 -0.39427387419879667 -0.31418077026655433 -0.2369520688707469 -0.1659279551387242 -0.1072130711095656 -0.054998252837319524; 0.23048879012851492 0.44890135070769654 0.6423928346963041 0.7976520307658997 0.9137275905467342 0.9891319821634812 1.0284839584148584 1.0337705976548779 1.0036548482802383 0.942831641764146 0.8515709743799998 0.7537797632592886 0.6764237805089223 0.6502943382838101 0.7025637760832782 0.8254763738275412 1.0004836529233871 1.2147433770426361 1.4369657737468327 1.6320685274731495 1.7766301566159088 1.8601986520698406 1.8789732130606231 1.8311437520663634 1.7069205253813917 1.491699506434832 1.1916553749158392 0.8239886009478146 0.4239211165727098 0.03671580835942832 -0.3074369994609883 -0.5972916199810935 -0.8282668075594427 -0.9999069072416281 -1.1090295892383772 -1.1600510310038399 -1.1538420587792475 -1.09841351268702 -1.003404899082263 -0.8852149726690767 -0.7604556113587705 -0.6430598159021123 -0.5316776123797997 -0.4200202556591445 -0.3112477837669191 -0.21529543792121858 -0.13672085128843992 -0.06796003920612868; 0.2301333938923407 0.4489019603251674 0.6448242779106704 0.8043446289327331 0.9278182193881169 1.0153367579278765 1.063198454052275 1.0730160017561081 1.0410237139312506 0.9724381939315072 0.8723262957323938 0.7649135000028894 0.6846168954860875 0.6605987476215988 0.7118604598640292 0.8340650206112777 1.011982960152405 1.2268935260596978 1.4476309091152006 1.6364162243620155 1.7708483811685964 1.8431015748276727 1.8460430563624892 1.7823408465418729 1.6469684510126823 1.4235172788698351 1.121730159568028 0.7627802667065955 0.37837634169492024 0.003641302627799731 -0.3377857872172318 -0.6294160755737388 -0.8629043607440492 -1.0376085182742925 -1.1495957559765797 -1.2065584836853045 -1.2136950202388699 -1.1830976311640635 -1.1139583875279646 -1.0123103980070627 -0.8948204782464644 -0.7736582613207498 -0.6489293808315713 -0.5155360444113232 -0.378464724140735 -0.256364160123597 -0.15799126043329648 -0.07534123416449019; 0.23206148226458145 0.4571053895988182 0.6576394316344508 0.8211164732248688 0.946584498522865 1.034591998021156 1.0796446807934525 1.0846556560061382 1.0440494143086032 0.9660683138955907 0.8669125419473984 0.766012157354184 0.6908725132065702 0.6673050889749942 0.711271927360977 0.8245104076175863 0.9947325606669456 1.1968038258894822 1.4038776780910238 1.5798194679525264 1.7031177266558508 1.7663832997541629 1.7589535609616922 1.6861119493669126 1.545518837073388 1.325873302498191 1.0388503757359433 0.7043285578797684 0.34485213265339953 -0.0075892801455074805 -0.33120038449717215 -0.611138837812885 -0.8375553099120273 -1.0068392370374892 -1.116136683673526 -1.1753188078275811 -1.1962487641880708 -1.1908949343195454 -1.1541446827613588 -1.0787697249461004 -0.9752257994520759 -0.8586986454837405 -0.7277571898521367 -0.5804687405479367 -0.4249286440778119 -0.2844421667662726 -0.1709903412013928 -0.07867871337814542; 0.24419817574771716 0.4816001034219493 0.6883487601028604 0.8533861529887329 0.9717319368057356 1.0442981301064318 1.0735843841518777 1.0648810374170559 1.01630855025352 0.937876869051629 0.8479686491695907 0.7574995058402678 0.6854779126763821 0.6570435749352634 0.6901697036761317 0.7877525970211511 0.9351553869855633 1.108360042333312 1.2866732944751131 1.440423449786838 1.5472580356659011 1.601748418862807 1.5966330034787883 1.536635020940506 1.4141461704660139 1.2201453427379947 0.9620578123991552 0.6616935873572487 0.33766997549845484 0.017145161469561705 -0.27944795814519613 -0.5411077569756648 -0.7574206962631048 -0.9187397379001893 -1.0246624367378843 -1.0872711017820003 -1.1218094064184143 -1.1359267631142271 -1.126061193896663 -1.0796020830895816 -0.9991361975183134 -0.895416145719004 -0.7635629710982694 -0.6098982603203105 -0.4475146032117248 -0.297856589183028 -0.1760537249209349 -0.08040018634257158; 0.2640884654405951 0.5140630541169131 0.7238362468646913 0.884988344551476 0.9905556142128827 1.0423912225580392 1.0499708981449956 1.0214307954775588 0.9630740337734233 0.8860245787578628 0.8056263787322279 0.7225845440019136 0.6502631746309369 0.6138957245720125 0.6330554664750397 0.7105072859327212 0.8305148161424175 0.9705973604692385 1.109483747846977 1.228355423840176 1.313348632202148 1.3633805396188337 1.3746851303982854 1.3486424903588088 1.2703870973475817 1.1234433511570385 0.907712637605443 0.6461356628533954 0.36284740446048525 0.07871335860449744 -0.19053356667056673 -0.4350903012950979 -0.6395073775857155 -0.7887402860471101 -0.8870839774814798 -0.9520990552617021 -0.9990414994519162 -1.031772316665768 -1.042221225368987 -1.0181688954518213 -0.9615787630659539 -0.8755093015313637 -0.7537466999121932 -0.6064090058058528 -0.4493834883874087 -0.29970271612496263 -0.17590036746611917 -0.08165370157946175; 0.28498973991446547 0.5472560101592842 0.7583648776534645 0.9128287648836985 1.0057061584901057 1.0369932718142376 1.019397408817023 0.9685736400475309 0.8962588943754393 0.8123705829574799 0.7318009744160606 0.650757652001611 0.577746336990034 0.5339557395394844 0.5368086757202897 0.5912971649724237 0.6837060346307087 0.7904211648661325 0.8885796650000591 0.9707869055550841 1.0325939123191914 1.0808960396757912 1.1189615112800204 1.1434674743019433 1.1311511599887338 1.0534455376714902 0.900319931818431 0.6841459444724031 0.43410145112505405 0.17545304659187871 -0.07356891315114181 -0.3058558727787122 -0.5000983793678841 -0.6392214353562293 -0.7324763214845121 -0.8012354399247767 -0.8560106040170191 -0.8994824557545896 -0.9205073645831663 -0.9088209613441331 -0.867432337040363 -0.7968225865518093 -0.6958329154389133 -0.5700504235133087 -0.42974730316272486 -0.2893539034181923 -0.17142724726043085 -0.08093420555388196; 0.296549567129654 0.5703849783867072 0.7897061126916259 0.9450332281550367 1.0314227450082858 1.0458660948695961 1.0021896571386584 0.921740513310636 0.8204519492801482 0.7128152396955464 0.6187314010559551 0.5351493142274897 0.4621983144822468 0.41587726276208686 0.40809338131327033 0.4447738932369829 0.5138817675205853 0.5905953443317823 0.6531626658329368 0.7046122145816187 0.7478531548690409 0.800982249449246 0.8723285041313241 0.9535719357297167 1.0163469923500899 1.0202824278396083 0.9399771192585639 0.7736344717026419 0.5483103292018 0.30070181265588813 0.06077808087965531 -0.16143029757272626 -0.34480628531454854 -0.47654875992597784 -0.5685554738771879 -0.6405461248552582 -0.7000978836800223 -0.7476660889829567 -0.7722481887904153 -0.7641764806494705 -0.7296418529744993 -0.6728677442912845 -0.5964030481823691 -0.501363297811854 -0.3891812543613735 -0.2704082235396416 -0.16655131895402003 -0.0798346530866328; 0.30148708703995836 0.5828654023903496 0.8136927709206143 0.976170985771238 1.0630804466379422 1.066198049781203 0.9977060730549472 0.8792313619369663 0.7354545263554366 0.5915359964105391 0.4731476368659214 0.3839373621825764 0.3129394530481252 0.26587625274199483 0.24872636211865953 0.26949770514212384 0.31996317898349746 0.3752810990579086 0.4135194752309647 0.44453689090297227 0.483382080201588 0.5535048835386314 0.6627585548900583 0.8027044485275914 0.9439258795573758 1.0314069156651702 1.019292608294586 0.8957879662559382 0.6867487131776387 0.44354568893246565 0.20562115510046017 -0.008870997541925038 -0.1825978809347025 -0.3089494978730164 -0.39977892579479146 -0.46969690554732135 -0.5303663589777962 -0.5784624316107646 -0.602426979620012 -0.5922499636987768 -0.5626420048176387 -0.5248595190841384 -0.4790088427624645 -0.4204792402817672 -0.34107643430826196 -0.24698492526764654 -0.15689300523032637 -0.07462916758421345; 0.3028017224075431 0.586544552967273 0.8268985684164928 0.9946387629928148 1.0807392952616868 1.0725064524661507 0.9779798149548462 0.8177121758733334 0.6278307229716354 0.4452013418506707 0.2989341887569332 0.19875491870499762 0.12708730388324702 0.08046183540344311 0.05813773338836601 0.06634797100429542 0.10122612603497924 0.14323287080182565 0.17364846091129493 0.2021687912864298 0.2526715750868865 0.3473543126652521 0.4960876246920122 0.6932019166060523 0.9053942101372177 1.0668589996213393 1.1157849626918297 1.02997747115013 0.8359731052734227 0.5999333242074067 0.36528417890385995 0.15555532220703955 -0.012491665542834963 -0.1364936265124562 -0.22622478083649425 -0.29010737788892654 -0.3449438321271435 -0.38821417026153804 -0.4093215825000243 -0.3997986424736262 -0.3803973223530593 -0.36607220277373564 -0.3520588752459828 -0.32669083758157536 -0.276953393262031 -0.2063808707340203 -0.13171515495457303 -0.06086072754907676; 0.3010461606438139 0.5819441756365612 0.8255383476425717 0.9954561166926945 1.0769472822393173 1.0535519272145806 0.9329389632496955 0.7392191037297665 0.5125073067674843 0.2950120290607255 0.11975424596522931 0.0011310577251356943 -0.07854933294342102 -0.13020645465376765 -0.1582093130427664 -0.15775974393563685 -0.1299483231094366 -0.09048348049271622 -0.051966247733642064 -0.008079486448208136 0.06316101820841914 0.1838398418516463 0.365491872208755 0.6026735492108277 0.8629598994981313 1.081153212241913 1.1855303932998644 1.141479323215209 0.9755193060784861 0.7586767364088639 0.5352678490043347 0.33242594654558955 0.16845096890253639 0.044633309210219775 -0.04435215205717115 -0.10280199391416667 -0.1492381761394374 -0.1880671016052103 -0.20786162670136754 -0.2028763455725616 -0.19511363310605684 -0.19882153955304352 -0.21105754743056082 -0.21553282263682852 -0.195418358714269 -0.14842644116296813 -0.09105915952591408 -0.0390044205458088; 0.2955075213896987 0.5663848542636967 0.7987216544547345 0.9594926437126668 1.0296650872176039 0.9910990255287062 0.8501499159318913 0.6352112866659019 0.3877907948945643 0.14808458740972918 -0.0532617043584079 -0.1973785528720183 -0.29325671927171887 -0.35378997347799834 -0.38338698723677195 -0.38083700157099665 -0.3465032131315751 -0.2948419267491915 -0.235502981286509 -0.16402072386126879 -0.06736342932141805 0.07608775869918326 0.2829348784803473 0.5438291310901133 0.8217931554645876 1.0607331356412797 1.1967216953493596 1.1959902838099221 1.0802811133363295 0.9063005870833284 0.7129266549443415 0.5300118606818786 0.3753226478827628 0.25387611839008817 0.16726721504291303 0.10985848008780456 0.06546767177016269 0.02536395791434327 0.0009062247202891022 -0.005666394109529294 -0.013418077643961213 -0.03420684340934903 -0.07127859625809559 -0.1052494556581483 -0.11355472315946649 -0.08919532916705472 -0.051167642828042696 -0.01991706435281184; 0.2809648943419486 0.5350712458425229 0.749161940873383 0.8952079498409219 0.9475607018233726 0.8931293157353684 0.7387823979463692 0.5122133795955364 0.25141398598373227 -0.009791889275919508 -0.23981380081767922 -0.4105524581670198 -0.521791773614181 -0.5853114459485519 -0.6049377476372193 -0.5839012737941166 -0.5264576514017929 -0.44852441569817864 -0.36272293076495904 -0.2605187464273912 -0.13040028114647076 0.03998945468282868 0.2646669257504182 0.5307333737511967 0.8005455910979802 1.0341886073400473 1.183253960658514 1.219826328735317 1.1594405980651628 1.0468182435762559 0.9073585517036957 0.763249666338793 0.6265494975526646 0.5094618689317836 0.423393504543479 0.3615574109713137 0.3097990082019841 0.25981870863190837 0.22164218225539428 0.19522872616557996 0.17033501313820867 0.13311590258288078 0.07336675067585414 0.009676077685406409 -0.030765085034234994 -0.03584412371424927 -0.020604656780475357 -0.006769959073132665; 0.25774012975611865 0.48918223781456704 0.6806615814863789 0.8074863432705445 0.8388827715443129 0.7680981006237833 0.6015406588847959 0.3625859970993863 0.08584020390864519 -0.1980854897403521 -0.453332884187915 -0.6458520517375623 -0.7662142380968706 -0.8187768927331692 -0.8108460584695144 -0.7542911269837462 -0.6617587593805125 -0.5480054662840163 -0.4248543806858992 -0.28444916825516703 -0.11551681551723578 0.08127582784749798 0.3117681074659126 0.5633406365952273 0.8071854363698927 1.021108579235887 1.1732514140648402 1.2444017947243642 1.2423245949820443 1.1982696177857846 1.1213156581879056 1.0266091058784885 0.9204803123517435 0.8163448818807704 0.728592056894507 0.6572684207014633 0.5896115937737785 0.5194626254821761 0.4581947231950826 0.4062162189612604 0.3584659734308967 0.2966122708231765 0.21048836793097633 0.11598319730039179 0.043228183190332045 0.005643721889469205 -0.002988142998560587 -0.001364380641177952; 0.2293566718778449 0.4344158824495984 0.5992529902482246 0.6991847756022118 0.7074141111012296 0.6203299042927489 0.44004948415943224 0.18368178495474585 -0.11534332730891417 -0.42400197650080085 -0.6996276494423647 -0.9047213317446319 -1.0218021458597133 -1.0481694448302945 -0.999111181342103 -0.8958043759435274 -0.7574920052211686 -0.6020043359025783 -0.43460920701778344 -0.25005482189141964 -0.042459473645343575 0.17608982488417008 0.40209598359006665 0.6270621277080666 0.8402201100795255 1.0321715878242967 1.1818418242472672 1.279244071724568 1.3270591534951524 1.3443575031225667 1.3293961376977048 1.2874148742779972 1.2232464653201065 1.1470020165334407 1.0655798087438442 0.9855846938083106 0.8944823591117843 0.7904490175019852 0.6903370332461344 0.6015820182119891 0.5224618465860608 0.4322837192235238 0.3200353908460596 0.19550476462523206 0.09348249774229005 0.0314029674491242 0.0062251061749086355 0.00014765751994996377; 0.1991115113820876 0.3728432311704634 0.5041250509639161 0.5727498461618447 0.556402485803139 0.4492556451129088 0.25071183295735805 -0.025706111958391207 -0.34714124066055085 -0.6751347260584333 -0.9631125826370659 -1.1685194506278451 -1.268631214221897 -1.258479406435871 -1.1578939510272719 -1.0023761951839927 -0.816071161415853 -0.6165030796388667 -0.4045017975749699 -0.17621037462595068 0.06461276989389653 0.2969945669869349 0.5119937006490145 0.7075519562167837 0.8886010606981712 1.057317727009447 1.2023914066588257 1.320663654685299 1.4095433088965952 1.476343925367306 1.5141056558017065 1.5201458660897276 1.4994170689637336 1.4568765647685389 1.3912121151560148 1.305925780629741 1.1899560729402119 1.0458618207292847 0.8955546064661816 0.7583697513892532 0.637590197224931 0.5143822438457029 0.37905004541343357 0.23747241677027014 0.12088012631171081 0.04598487594287532 0.009703817479887938 -0.0015906443996861056; 0.1660979941488264 0.3063438520494887 0.4026352279453095 0.4400508574587691 0.39853295962441665 0.2699239929006282 0.04857880832953902 -0.24770679560243378 -0.5839743240134075 -0.9211141865673497 -1.212282146572071 -1.40688865831804 -1.4806723336577987 -1.43128242808901 -1.2783279433510877 -1.0692795928211296 -0.8325239371105443 -0.5844948562399211 -0.3290962412400327 -0.06697669751401375 0.19187424577567916 0.42468151574378404 0.619919898232925 0.7863858676379308 0.9387893029300775 1.086516386378412 1.2271744855047941 1.361367010686283 1.480526816875761 1.5834381908785278 1.6605572669385997 1.7065248005876508 1.7225250082228105 1.7082854142702992 1.6602572727727611 1.57301813702681 1.4360138056813787 1.257234955034333 1.0592956811059862 0.8712582795258175 0.7006578382779578 0.5368007149934341 0.3802150255699084 0.23586452016986711 0.12172162490703649 0.04676999335681312 0.009087026770645384 -0.0020717219232227672; 0.1249162138140006 0.22584862389056948 0.2839666588709371 0.28644694274132015 0.21873848855563696 0.07442261933135369 -0.15949763559369304 -0.463598928786382 -0.8043786686933345 -1.1425638891361114 -1.4262413243781549 -1.5986372638714998 -1.6380471681351205 -1.5466891717050122 -1.3467912543319696 -1.088619739081333 -0.8007956269774802 -0.5049881496827973 -0.212210586480445 0.07172459126208149 0.33428341158048624 0.5538969554351832 0.7234695053178464 0.8636675055215242 0.991231712866265 1.1193949885674974 1.2527508418154816 1.3965561062637817 1.538694833017479 1.668200055981222 1.7723584459732624 1.8468850117169338 1.8894204159356176 1.8971942256971341 1.8622866104436875 1.7722920145225416 1.61733243214922 1.4121302692883706 1.1749664293235547 0.9384617519148366 0.717552452717027 0.5124081026670249 0.33621855298365716 0.19407085095257945 0.09035926622544244 0.02445687237030624 -0.005907562452238793 -0.009762026027649112; 0.08092027385448546 0.13635773369702828 0.1537750282337281 0.12060831607106594 0.024279946579141228 -0.13563453908242384 -0.3719086840575867 -0.6687980410490496 -0.9995805628384026 -1.3241358056013066 -1.583814597069304 -1.7236205053641127 -1.7260746189856209 -1.5951404841457146 -1.3538627388173385 -1.0530139354562686 -0.7260949413567344 -0.3976564448363887 -0.07759032305425753 0.2204396820546456 0.4790703420044476 0.680915593494539 0.8258907745319803 0.9407906447723399 1.0447283320344847 1.1551371472922936 1.27985886175271 1.42743212777109 1.588844558472841 1.7413052831811366 1.866717341124187 1.9609388707094546 2.016132033915316 2.0320067505607957 1.9968924479455998 1.8989423475613054 1.7328486937242278 1.5146425308079823 1.255826242021953 0.9840278600864107 0.7213172842211657 0.47913990026483033 0.280275474171892 0.13369559159638347 0.03874202519409259 -0.014853147308390031 -0.033598361228969274 -0.02586325676979638; 0.02794883506122277 0.034700065163745596 0.012788950479099052 -0.05155079487274001 -0.1722300278309666 -0.343389941450413 -0.5722986776456965 -0.8494371572059517 -1.1534106593778326 -1.4465111453923725 -1.67049396340163 -1.7716416166118396 -1.7322566133653692 -1.5651574571879294 -1.2924955919080303 -0.9625876016180074 -0.6137416589941552 -0.27029142291382857 0.060970984566674956 0.3609638602017775 0.6097602926275395 0.7979626943551191 0.9261995053861818 1.019623469856982 1.1014919908987502 1.192967540446801 1.3071343289247364 1.4563061718107821 1.6348667624713071 1.809835954010892 1.9548302387589083 2.0623339466195674 2.119077864571967 2.1285336680401525 2.0804552223845327 1.9681427865574272 1.7922777766660642 1.5670084537927749 1.2997124901284247 1.0106474775234564 0.7223489128039671 0.45557198470220717 0.23427156515826195 0.07567823409079621 -0.019511231185598287 -0.06576785903048273 -0.07215306388423695 -0.048606898431894606; -0.02765959127037319 -0.06752254333792475 -0.1267667143872052 -0.21855231192875063 -0.3542835491299042 -0.5268437694463747 -0.7416358178805947 -0.9928306577908369 -1.2584435397380782 -1.5024096146927706 -1.6765199555295773 -1.7340440721007888 -1.6521886533999324 -1.4518584606279468 -1.157943849364205 -0.8164127905575063 -0.46355336041742107 -0.12148440507384309 0.20273976895331686 0.49226650738422634 0.7270721895741945 0.9044910386650971 1.0249214122148929 1.1092980102480312 1.176006083737476 1.2458630119267466 1.3443766520470493 1.494062586974992 1.6846713899882164 1.8768018198716407 2.037631434976055 2.152898003984633 2.2042471200569524 2.197539795730988 2.131035497976535 2.002416562328761 1.8145346280637573 1.579469391974071 1.3064589137796123 1.01207094739378 0.7126666558498024 0.43430715237374795 0.19820465851131602 0.02896153575739153 -0.07264401991890554 -0.11710524260725406 -0.11340941760595019 -0.07238897578387682; -0.08241450363319594 -0.1650632220894713 -0.25388210254307103 -0.3623833314460703 -0.5032632109571529 -0.6727907513391157 -0.8700539797296907 -1.0877263026630115 -1.3069722355597135 -1.4933983229394394 -1.607345006677459 -1.6135491468053926 -1.4893614544229943 -1.2583625902599869 -0.9539170267994852 -0.6184774507107131 -0.2805811375627171 0.04168307091252923 0.33950217191189597 0.6051799550253236 0.8232766434798687 0.9932759076809918 1.117040590772906 1.2081854686924691 1.2746686481419576 1.3337503593304667 1.4154235081703215 1.5528090821377483 1.7357101159101225 1.9274877501870726 2.0919050791467786 2.2114839293602744 2.2644475558651602 2.2484422556558323 2.1652580825750065 2.0173517473940823 1.8103645354768156 1.5598313724424309 1.2789671072389668 0.982625287639715 0.6818235955801392 0.401903608165236 0.1649727888692088 -0.004298873447657819 -0.10928714636991364 -0.15582320295849678 -0.1486640552111194 -0.09323694920667454; -0.13692308295105915 -0.2587070954337544 -0.3660493267523953 -0.47710965807625894 -0.6112993323916139 -0.7709584553490109 -0.9482262241625138 -1.1315710738929525 -1.3032208348318737 -1.4302495654484337 -1.479937241211999 -1.428526707001289 -1.2634696488852706 -1.008154166271318 -0.7016430816970545 -0.38256294095813004 -0.07677771240265473 0.2058024647994756 0.4618307868153312 0.6925570263512455 0.8885158801348368 1.048740287417887 1.177519429584973 1.2790157528897883 1.353573459658591 1.414127771800926 1.4827530613843896 1.5986949528691534 1.7614558645792777 1.9419704326402711 2.1023021004828077 2.2228742008654883 2.28126008180116 2.2667610431503564 2.1775985040182437 2.019186572724878 1.795724418749443 1.52601207202497 1.2286709555941433 0.926273658573383 0.6325842958358655 0.3643636852075848 0.1400191977191285 -0.022396262728097253 -0.12732969601976973 -0.176573252695862 -0.16944328667841918 -0.10556686839003496; -0.18211671673912264 -0.33502671018757296 -0.4540945081535071 -0.560561124662012 -0.680368968835457 -0.8232380620812362 -0.9758341364922801 -1.1236196278710082 -1.2494583898452976 -1.3236351082633184 -1.3172880695456766 -1.2106468918692244 -1.0074047915607958 -0.7361827072807643 -0.4362862167963288 -0.14138957186417725 0.1229834707686138 0.35583585187776895 0.5610756966199432 0.7447421470455117 0.9058542424180381 1.0466531010137812 1.1708682330457587 1.2739719028808154 1.3526836208043682 1.417841816750596 1.4845882980336362 1.5864877699420579 1.7301657400729449 1.8955019443175463 2.049110790107295 2.1701782408950834 2.2363578811475704 2.2351963188552397 2.1588451850334365 2.005794791883889 1.7759272678954736 1.4904813014633953 1.1760221775161115 0.8667355256879532 0.5825916915982472 0.33130040658643267 0.12151027519937514 -0.03605194934530043 -0.14093765422909116 -0.18935646644077736 -0.1791998693376537 -0.11067209692528007; -0.21682809637845063 -0.3924108755903818 -0.5161231934265074 -0.6102498973155348 -0.7066686454597685 -0.8229404542426313 -0.9470721694323132 -1.0634116383898862 -1.1512522635661593 -1.1826449425660073 -1.1315429990866943 -0.9819199821039262 -0.753266500350333 -0.47776242274683045 -0.1936700333685986 0.0696599252026377 0.2892108379040822 0.4677627660480422 0.6151606803082207 0.7419742374745922 0.8563161169847773 0.9652273550088896 1.0724360003428608 1.1697933301194867 1.2507719485649615 1.3205331752149263 1.3932870393819137 1.4905631551217533 1.6212713971428645 1.7737087578176058 1.9218010190702493 2.045667225594021 2.1262169021441446 2.1474123629689816 2.0952212274654562 1.95934105099695 1.737246560108905 1.451026122868473 1.1315029896268636 0.8208414602206312 0.543250397040489 0.30652805297935265 0.11159172939121755 -0.03926198750231576 -0.14025990695609133 -0.18363666000747048 -0.16962601261600968 -0.10301559506270065; -0.23268785896156485 -0.41901924240780947 -0.544292083504707 -0.6278813898096333 -0.7001815228339222 -0.7835436810287483 -0.8758871142404023 -0.9612127474196962 -1.0166704143264906 -1.0157525751970176 -0.936386416160398 -0.7651846798502346 -0.5256288014224608 -0.2529894923859628 0.007446911932541268 0.23324077020275713 0.40660243800602225 0.5313418189830315 0.6231907216169733 0.6937816952393261 0.7581912440632389 0.8260563430214086 0.9032676193940004 0.9831805916295476 1.05728038407589 1.1255827195521368 1.2024890705581677 1.2983057218447842 1.422254000530152 1.5706355495604287 1.7241584656749522 1.86142733706922 1.9652503769393703 2.012754167074242 1.9867066051694051 1.8745145370892167 1.671393237805016 1.4006972215390203 1.0933968952756297 0.7934923043320088 0.5232879428825298 0.2940008779197417 0.10730225353221912 -0.035032639209535824 -0.12740695795920995 -0.16405484737301573 -0.14949446168950783 -0.08904548962000869; -0.2343673944006283 -0.4229120106675896 -0.5476583135146702 -0.6206313699780284 -0.6704056430091229 -0.7197343954742734 -0.7764416258818273 -0.8284138568222014 -0.8585241493156378 -0.8365916467899356 -0.7424620191086378 -0.5657688003983605 -0.3310354517702326 -0.073434805441341 0.15790102541509876 0.34597146370460835 0.47522124754231376 0.5504780475842274 0.5929251924693395 0.6147718443283492 0.6351315610913785 0.6597707004303978 0.6983119389378522 0.7485982363434945 0.8051138476262716 0.8622136031942897 0.9333199968362146 1.0263464386489818 1.147650577596024 1.2971455246844625 1.4629626467494998 1.623448080003371 1.760402996645559 1.842555026982161 1.8452762657361752 1.7605817609985217 1.5870794793022573 1.343070895467245 1.0565298166116912 0.77284779793943 0.5150442816313637 0.2927587939939055 0.11097873706408894 -0.023236373494787778 -0.10474633053087173 -0.1336080310564772 -0.1211074179376196 -0.07092292766934072; -0.22683904185678358 -0.4117773014875915 -0.5338127620934318 -0.5946035714334995 -0.6219021874732573 -0.6412353379810382 -0.6667553246311115 -0.6900635658807892 -0.7010173058695929 -0.6628886048721071 -0.5607212033430631 -0.38832053342508116 -0.16832525872507145 0.0691511777104648 0.27406001983456474 0.42614731096282826 0.512574086326615 0.5424150756324294 0.5392258584954978 0.5156550141296805 0.49514162146443863 0.47806551986791496 0.47805823373645606 0.4935730185347082 0.5239360893108022 0.5607918441903206 0.6176220399458505 0.7020834933553013 0.8197655083910411 0.974940914386742 1.1614489370910661 1.3521836206586304 1.5231629745857422 1.6429349017803097 1.6778681979400059 1.6251219136426964 1.4871303921556471 1.2749412421383486 1.0196728411361236 0.760876110915817 0.5199717824676418 0.30783050809774143 0.13530625349620995 0.010323793084570713 -0.06414528334109473 -0.09259241039504079 -0.0868204649831457 -0.05134245873007965; -0.21310830874720496 -0.3876201213091618 -0.5032415665102461 -0.5577582719490465 -0.5732307217276775 -0.5721269046672163 -0.5728465052648308 -0.574395433778138 -0.5695158400076987 -0.5165860669388354 -0.4066437989301752 -0.23807953663282233 -0.03318255923394563 0.18045143283420417 0.35666330283542347 0.4731123716103548 0.5188814637443425 0.5035650957163699 0.4552217230433745 0.3918663593748037 0.3357237819552195 0.2825037623481919 0.2468179102903589 0.22844110409222632 0.23184921292419722 0.2469914647842444 0.2870413410548731 0.3603940416322589 0.47557617292502646 0.6390594350104252 0.8482448753923788 1.0722352735453817 1.277016887782924 1.4311126724442074 1.4978971469962197 1.479991454950227 1.3816007433959008 1.2067649544813552 0.9891036200198037 0.7613939448829168 0.5436819754468171 0.34980815640871543 0.1892778435816133 0.0698778933472429 -0.005025672860895349 -0.040577862467228214 -0.04491820025663722 -0.02700140532060884; -0.19614799712150915 -0.35922853200103627 -0.4685899391498285 -0.5196828192463716 -0.5309450160251704 -0.5214999053767457 -0.5101147315061443 -0.5000073161644627 -0.482972491301144 -0.41777430998436565 -0.2977944303281449 -0.1267775309990522 0.07006880575728369 0.26063184919185955 0.4050653874971247 0.48541961106169296 0.49337832366412476 0.435449453758325 0.3435370897217165 0.2442093353759338 0.15586714936331464 0.07419307447584197 0.00839064788368874 -0.04020296588642679 -0.06008840855428662 -0.061486296300111175 -0.033892579018304995 0.03434285887937208 0.15258725164038164 0.32745448796083837 0.5583145559976751 0.8098141874756339 1.0391650622607 1.2162227016527227 1.3107388175815908 1.3268592117410236 1.268670267826523 1.138132771128435 0.9648599729818541 0.7773475020982372 0.5923263786858628 0.420986970028171 0.2687299965651141 0.14905510878078596 0.06885678300018537 0.019325874212764115 -0.003520471764878064 -0.00538602653592651; -0.18102386506608603 -0.33400887904746823 -0.43674336830588373 -0.48667163611603786 -0.5010919313743402 -0.4956776742969352 -0.48462060493855924 -0.4696920085288885 -0.44103241925297537 -0.36399187910611386 -0.2324965458613548 -0.05827700937917978 0.13159196740278384 0.30174247015066286 0.42000835112797397 0.4694534924724129 0.44199577830512804 0.34527790147159476 0.21514524946639607 0.08277597584615114 -0.035682618356194074 -0.1403201069593761 -0.22898992522116804 -0.2981308338332932 -0.3317794467364974 -0.33839165614817485 -0.313599934574621 -0.2425164421527456 -0.11723570789362503 0.06936412947081143 0.31573194434631074 0.5811111561188325 0.8204875736134405 1.0092007555839841 1.1236678711888621 1.1667751000561895 1.144324426926462 1.0621819278492992 0.9407996863677266 0.8012373951354596 0.6527568361339087 0.5044227944608286 0.36306393545154203 0.24336981828169735 0.1543087456575109 0.0874483215332447 0.040064704050758314 0.014015727533348885; -0.17423642862836633 -0.32432606178640644 -0.4272866838254305 -0.4811437470465423 -0.49995818459092795 -0.49997524173643565 -0.49148110221887353 -0.47268329909649126 -0.42915650809637235 -0.3385166483590461 -0.19886339064963438 -0.02801399019440153 0.15031070780309044 0.30509844217462573 0.41090386526534306 0.44154416570797167 0.38396752719254407 0.25246172006423107 0.08934365644390709 -0.0716935433336437 -0.2160471864697252 -0.3390320594775737 -0.44340292912733237 -0.5229493431274601 -0.5623513819913252 -0.5671499169816436 -0.537935635576753 -0.4595450949742636 -0.32509502613439273 -0.1288723953398135 0.12012789604951327 0.38357102825155315 0.6208107955669693 0.8097517089931506 0.9334838110662335 0.9964035110939486 1.0081394628447755 0.974472034609328 0.9060235092640728 0.8154276008742516 0.7025555511439675 0.5759570734787435 0.44767090327547887 0.33143298014506384 0.23717443532594176 0.16006131759472053 0.09289585415829867 0.04027144255204177; -0.17684528205059286 -0.329382432497961 -0.4364938800420878 -0.49733759068709366 -0.5201387812074743 -0.5212857260391087 -0.5078367994433733 -0.4789605523438417 -0.42172392925892155 -0.32465167095933983 -0.18655293964796066 -0.024958672394927345 0.1388361462236717 0.28029722215231984 0.3804651320636162 0.40469606077801085 0.3308538713654743 0.17453469374569486 -0.016326044069055794 -0.2043666484891755 -0.3724212559863471 -0.5080916876207123 -0.6164882990433371 -0.6933740692117534 -0.7300404080477545 -0.7333659136827246 -0.7023590167077461 -0.6217551353530676 -0.48204394559091185 -0.28215874542997704 -0.03860824824400473 0.2146435052340916 0.4400533033960377 0.6189759430513858 0.7452411929410669 0.822440962811498 0.8622354381415674 0.8690318947619773 0.8470590895330712 0.7978520433473851 0.7158915304632116 0.6111135020814685 0.4984092461523195 0.39116062958273234 0.29899698904827277 0.21804467415675924 0.14059043402333568 0.06763203023658886; -0.18618013882930817 -0.34134027052342425 -0.4489749100596314 -0.5116101338846597 -0.534107892173516 -0.5320131965499157 -0.5085967620980372 -0.46788523627924566 -0.40196937225923546 -0.3079035795470122 -0.18283961496203857 -0.03656470985860989 0.11278127077839328 0.24299148687525654 0.33605090903630286 0.3547228701355694 0.2750394261259571 0.10679878989135702 -0.10251649083879566 -0.3091821843168853 -0.4932159216756074 -0.6358325373416014 -0.7410781875788645 -0.8067731288150298 -0.8302569633585244 -0.8250290178486485 -0.7895405799263276 -0.7093332899940118 -0.5745068758313204 -0.3866545196166185 -0.16117795963156886 0.07083831378463873 0.2747356284889264 0.4351483547379892 0.5561179790792523 0.6429068526649353 0.7042249303689867 0.7399008491596883 0.7513035148430205 0.7342828151342787 0.6808119979307498 0.6022140621350875 0.5106880342891762 0.4195778000569038 0.33999987778870594 0.2625872135033003 0.1772390867847585 0.08802353065210868; -0.19429293547057783 -0.34919229261713924 -0.4510098555851533 -0.5061458844543003 -0.5213073034258223 -0.5113473223582428 -0.4785191320557934 -0.43041369385704725 -0.36142237407566213 -0.2778204816608332 -0.17521191256924945 -0.0537906121661246 0.07838662230245422 0.1998228677133498 0.28679657159272665 0.3000633252591164 0.21722725949022265 0.04618246867171159 -0.17131225026809804 -0.3865224108746784 -0.5751178346038747 -0.7160497576804999 -0.8121646572341942 -0.8626898344490277 -0.8682199024575936 -0.8447567785244784 -0.7999955049850647 -0.7195207507748315 -0.5951413557707 -0.4291887037938378 -0.23510788212360162 -0.040736791444129894 0.13320386362273176 0.274184689183651 0.38678539870086953 0.4788100719186702 0.5517615690054196 0.5999532322046814 0.626429255740738 0.629641529783864 0.6005325559102638 0.549899037160423 0.4847057440404992 0.41548759717720657 0.3496432648125869 0.2746275952134384 0.1832218299812719 0.089497614702866; -0.18854748719324965 -0.33669697418767186 -0.42970040657409647 -0.47291315894765884 -0.47640434159329703 -0.4564340148237122 -0.41751753554992793 -0.3653862981570702 -0.29733318245030166 -0.2262042179703915 -0.14328061304260847 -0.045416740654651656 0.06472650236675408 0.16793619608084817 0.24026222903279687 0.24434094897356973 0.15723874051317502 -0.00838956101315896 -0.216761775060635 -0.4232058488048183 -0.5987268641445389 -0.7240114543019264 -0.8005641828486605 -0.8309317032095084 -0.8225493315017257 -0.7829491945182225 -0.7298576606857012 -0.6548082343993856 -0.5494374379098592 -0.4145706959080228 -0.2586869627982752 -0.10808673256271936 0.027921747114206478 0.14407185974738576 0.24500513763853377 0.33783715341070253 0.41387825825510044 0.4635440929774046 0.4937366148766301 0.5061761561177898 0.4942040926568733 0.4664140306383407 0.4271428415210121 0.37967200794815875 0.3237058008592046 0.25052049001488425 0.16302684662842967 0.0786461941246193; -0.1647642200142935 -0.2895547943965154 -0.36257964806989973 -0.3914697094253936 -0.3886837233517783 -0.3658561122429588 -0.32809154660168743 -0.27739363925010013 -0.2165001338235831 -0.15933559879927123 -0.09275113045106373 -0.015608555871188964 0.07043839066718473 0.15081240257894474 0.20405352335009921 0.19767982996552227 0.11060530246891735 -0.03993322390640222 -0.221119249710633 -0.3973075634755216 -0.542009953498794 -0.6445690679314771 -0.7013560194459284 -0.7122767439680082 -0.6925901690104038 -0.6465695672411929 -0.5929608625658005 -0.5291743474905327 -0.44512380509989685 -0.3444645681846359 -0.23359218867821735 -0.12986824535942548 -0.03238129764778501 0.05750559966014323 0.1430025943386937 0.2265840752465958 0.2947082064521748 0.3386090278348607 0.3650310835110921 0.37729689533808547 0.37449099119194557 0.362530264212113 0.3448738225454176 0.3170108593203505 0.2710587354067265 0.20527814656836432 0.12993365663912704 0.06082172582854411; -0.12394011951966195 -0.21470134213003253 -0.26413351723624384 -0.2800872452911396 -0.27346726938846083 -0.25144941839374446 -0.22225089771323328 -0.18182509339257438 -0.13323787269920892 -0.08906888384282018 -0.03964566337070431 0.01485549622553169 0.07611033625171985 0.13326231497547567 0.1640851227244468 0.14718384024193276 0.07215984057074822 -0.044714457765848516 -0.1790130619780615 -0.30686476796541784 -0.4073689205342713 -0.4788051240663911 -0.515604464801703 -0.5147377988450887 -0.4923228258663611 -0.4539912606750856 -0.41054711314752623 -0.36371481586149373 -0.30592823536552494 -0.24174934518668942 -0.1754128812515887 -0.1149164533957625 -0.05334873471828675 0.008717980548894605 0.0732323818024484 0.1391976552251681 0.19306922589730224 0.22584798257303304 0.24235073865920476 0.24979306213047958 0.2519463929764859 0.25189775155309607 0.24774075325752806 0.2309232353963414 0.19416517055816848 0.14249626139024107 0.08709697502595712 0.03828111562175687; -0.06682066304687494 -0.11567643139681641 -0.14226015583295953 -0.14980964980901854 -0.14332647560239772 -0.12674906787810636 -0.10885020367220964 -0.08724376187223411 -0.06184553747131714 -0.036481997065948006 -0.007603050531553751 0.02303269708973007 0.0550149518859174 0.0835897794006752 0.09504027855787589 0.07994716145599884 0.03658700333864874 -0.02599314824275477 -0.09553010740118335 -0.1620936633601367 -0.21546943167670712 -0.2553378751097966 -0.27516675843720634 -0.2709780280263805 -0.25443805227463534 -0.2327878037188901 -0.208085752900938 -0.18299563558535312 -0.1547465425643167 -0.1252321173379945 -0.09562594216955322 -0.06915538319132856 -0.03896372325360012 -0.0052568446479373246 0.03096457238464964 0.06741025642003524 0.09704298756333032 0.11518303064327141 0.12252467758054306 0.12448041922551237 0.1262333976669055 0.1293348157152387 0.12970601883930274 0.12015114875565308 0.09835476292790399 0.07007502445628173 0.04207368794599776 0.017366054459406678], hyperparams = 95.67043675041819))), instrument = (lgR = [0.11090091779269576, 0.11085222139182901, 0.019363620118572348, 0.15233453592868115, 0.17280757751127096, 0.0674967031641901, 0.06268919704313253, 0.12957646431758185, 0.08443136898254801, 0.006523337682730155, 0.09044830316089439, 0.05951656430827086, 0.04564799035990572, 0.10459142436411192, 0.04660583215894767, 0.04116117276370781, 0.08802082402177579, -0.059406041996634525, -0.12470927866115537, 0.06370700519829979, 0.17410302304508377, 0.048395425327887195, -0.00176464771917044, 0.008053111066798206, -0.23591342753725913, 0.07817585974903712, 0.0618274702052786, 0.11141823929896544, 0.018587124704267884, -0.20191379554085073, 0.0203153537277368, 0.01152641476051053, 0.0955198858778476, -0.3470945594279216, 0.09984828552118817, 0.030661308685990624, -0.011069920936474237, 0.08707509173096523, -0.2823274404256719, 0.05568531255880554, 0.027698076886554557, 0.12320985475411698, -0.1864960693407447, 0.12257185744634448, 0.05906272995552356, 0.03952788772599092, 0.09917563163676571, -0.17591022536025405, 0.15857541918905096, 0.08337843071990275, 0.051691760813484165, 0.11064923700075616, -0.5274815715623389, 0.031499295220503785, 0.1739610192444668, 0.0712278163224279, 0.034530012203433234, 0.1414049302250429, -0.41383883802531946, 0.012282997122552049, 0.18746577791458827, 0.08975434511620653, 0.11944430425335313, 0.14024473670401966, -0.01273376575903357, -0.2199457783523709, 0.2310121304861817, -0.11668888341628, 0.0872395420495284, 0.06907543181649473, 0.1546689900833021, 0.13530012621132997, -0.28550615364670434, 0.2297137828528925, -0.0952541286074639, 0.07564810915043278, 0.04477540636844687, 0.21344069468218138, 0.24597543956634904, -0.15214606240073378, 0.0832086602547666, 0.07562814110737448, 0.045202275253559264, 0.2472304573600481, 0.27056053268903124, -0.9474922352558243, 0.1534692356694259, 0.0960841598027496, 0.08364005362276201, 0.2250917405363579, 0.30119255652059473, -0.16985728768023672, 0.1150544447670043, 0.10851459113632556, -0.010251727222650933, 0.18150796135313024, 0.3577366173926499, -0.09719826446651178, 0.1949552855764911, 0.08319860899659297, 0.18842033671802277, 0.4001256471082541, -0.3008843260504382, 0.21800423365782318], lgrat = [0.009657141814684895, 0.04050376065648002, 0.012055034535596318, 0.04723781349023839, 0.027357797999027066, 0.04401936872492482, -0.011585543209288516, -0.020241266751320954, 0.013853913270400512, 0.03152171751131665, 0.03626264950206964, -0.004002924098509981, 0.0019524384141789662, 0.04557376611995977, 0.04689587233693882, -0.04535110995741706, 0.008392362282210821, 0.04602294219722357, 0.03476338874403365, 0.022972700145582725, -0.005153757586936929, 0.0355568780265424, 0.03931427708581918, 0.017420309854737893, 0.03568019577443648, 0.017147282949322808, 0.01351089844893255, -0.02229945798194918, 0.056312743482790965, 0.05272323090271892, 0.031929774447193075, 0.024214541914140963, 0.03430108398773276, 0.056817406716258775, 0.033559276901161866, 0.005536396610988331, -0.02212375881218565, 0.04999808466000309, 0.049912436425950946, 0.00014496172266909135, 0.0642646415296659, 0.04055247357022486, 0.05096242427049344, 0.058143652336753324, 0.01791724552194477, -0.031126416714188525, 0.05396975459437567, 0.06519065555476201, 0.020171821586354853, -0.007137145904665292, -0.044366821216570006, 0.044773323936341015, -0.13933658909482816, 0.040933873350602897, 0.056598128344910965, 0.001954644585288231, 0.000977470864534953, 0.04671131428099377, -0.11720660263178126, 0.044284732591251263, 0.057633756880261705, 0.005543212517712955, -0.08332078943379308, 0.055455710351477464, -0.02685693468576179, 0.03501468415044047, 0.03871341946594033, -0.12562307489789043, 0.0012014961056718112, 0.0014464564192219788, 0.0424619074075907, 0.008853285372093405, 0.0747204559302621, 0.03910218257295542, -0.07429681448992274, 0.025718703600075516, -0.007833840738856271, 0.01970556936948209, 0.020507259568529123, 0.03279874442432364, 0.01289548328874164, 0.002587145776194832, -0.06185505481801503, 0.016409595157757216, 0.02884747950231614, 0.051514147719970656, -0.010346712982038247, -0.011849637981575747, -0.017593144993444713, 0.04735431494017564, 0.03993448479265701, 0.05728068551389925, 0.04705504884871352, -0.024832428161245697, -0.03250709956221439, 0.07189574194220831, 0.06399908958404427, 0.06399801901833141, 0.08639852985303771, -0.007223282825438816, 0.06089895690575045, 0.07993295720357287, 0.03147640961042122, 0.06111028487701381], gpR = [0.0, 2.877575114050692, 0.0, 0.6431448540018009, 2.772689095392043, 0.0, 0.5079822147447365, 2.672295615609127, 0.0, 0.4022841603496329, 2.418677970022576, 0.0, 0.42024013232961693, 2.2836729610003874, 0.0, 0.43829808133762566, 2.035182703410417, 0.0, 0.36501888619053935, -0.8597443253840278, 1.9076790500020873, 0.0, 0.33771870279127547, -1.085213324107847, -0.275652721251932, 1.6227512773441413, 0.0, 0.25927351414851857, -1.1040332008561573, -0.2591584998942378, 0.0, 0.25704547737838573, -1.342238599150718, -0.2207311795392657, 1.2007419176254461, 0.0, 0.15207978313491405, -1.3982550365950939, -0.2632847173978097, 0.0, 0.2517063397673672, -1.5452675951152417, -0.33266439608388504, 0.7505392561064012, 0.0, 0.19253054189456462, -1.650318417841249, -0.38005631320553607, 0.6658203271714952, 0.0, 0.24860102059284422, -1.9204822067769016, -0.6671540542461076, -0.5103309204200135, 0.33494146962061133, 0.0, 0.2072677378900285, -1.9631122969272556, -0.6811614361065794, -0.6022807934372569, 0.20731022895819723, 0.0, 0.2222725553823004, -2.1926664089245422, -0.7221248655719605, -0.8416412316888474, -0.041950850697275284, -2.6164556247894555, 0.0, 0.2557569984033038, -2.317632405146124, -0.7391614229335752, -0.9379567396464611, -0.14145407083180533, -2.6943598314847, 0.0, 0.312179958128385, -2.810041192025731, -0.7300063789987553, -2.0029169005267136, -1.9122365736246525, 0.0, 0.40544236855278004, 2.905624342202604, -0.6884617855283666, 3.060868548938119, -1.11926605089114, 0.0, 0.5478303360505086, 2.2690588788852524, -0.6269379518968338, 2.306110508323279, -0.15285949962776038, 0.0, 0.673324786738924, 1.8367202388168287, -0.6153647352239098, 1.8809042930927358, 0.20846551556514625, 0.0, 1.6631230255691267, -0.5266274685744822, 1.7630542714328181, 0.45800453639255845], gprat = [0.0, -0.048218440782306006, 0.0, -0.0916449123770723, -0.045080657734966126, 0.0, 0.0527714923084593, -0.03978977293305042, 0.0, 0.05819893186850529, -0.05988331867655435, 0.0, 0.05005894870730175, -0.03622821856138499, 0.0, -0.0685295652918875, -0.06874991483269195, 0.0, -0.04812112315178414, -0.042780019424040604, -0.04726312892131102, 0.0, 0.02570024648072568, 0.0353691167149462, 0.03840150936706128, -0.05855591122573535, 0.0, -0.005891201699310445, -0.014740054421417011, 0.029813554133209862, 0.0, -0.05290023320589178, 0.035439119742154974, -0.00962538082385093, -0.057393037179750694, 0.0, 0.01701693807859642, 0.005277848893122473, 0.022021174641824067, 0.0, -0.06002680117979719, -0.04158669624076739, 0.02770831658488134, -0.036400863991965675, 0.0, 0.03235358537061516, -0.02390397613699784, 0.029585753558163008, -0.05812992000826294, 0.0, -0.0463740198162019, -0.020595267972556997, 0.04349158577881235, 0.017391695569953028, -0.04315992640849885, 0.0, -0.01008761140270788, -0.04916985166133849, 0.05967628584993152, 0.054046932878856854, -0.01387548069094719, 0.0, -0.008840876230268968, -0.09203025261196272, 0.03975159778045811, 0.06279175585749337, -0.027060891593691586, -0.6630425103340774, 0.0, 0.033117918230343504, -0.05453112246968044, 0.03634094028017244, 0.05103414708577949, -0.027243727646153508, -0.24989772581566827, 0.0, -0.042150896842404924, -0.07412881136228523, 0.047747085921161773, -0.016321091655794245, 0.2255423410224755, 0.0, 0.009569070738608087, 0.05713168229375931, 0.016087604129395677, 0.015861683619422636, 0.15882556695159575, 0.0, 0.02731915111644211, 0.1758086228969238, -0.009915103279776863, 0.011765553171297776, -0.12377225745141612, 0.0, 0.050611203794061047, 0.19380092123960463, -0.01195731012255711, -0.009448739841098232, 0.04882774962192001, 0.0, 0.17419600265797033, -0.018809258366826377, -0.009995026331773415, -0.018549254832586903], dRx = [-0.008109248742657145, -0.05222715191834749, 0.032403249138496584, 0.000448839844907692, 0.032645409702015994, -0.11053908161301133, -0.03262153171737247], dRy = [-0.037052937843712906, 0.03483760878329025, 0.08797993002374795, 0.0005770714559388448, 0.04414294957585141, 0.014475525070373935, 0.008944396253946918], dLx = [0.009033029854454252, 0.021654590516214003, -0.029962995858560222, -0.051239097408931435, -0.0029268046412065287, 0.13957362820680796, -0.0339881544838362], dLy = [-0.034323835120628615, 0.037978913770272266, 0.08761801425103502, 0.05638696034272269, 0.005626398160782996, 0.0045891779724163174, 0.06596623389304535])), retcode: MaxIters
u: [1.249432583788386, -1.640107362368866, -2.492168071204298, -4.139021364876457, 0.006965121540858039, 0.01581694263135559, 0.02390369821586987, 0.027025297059447218, 0.02823409862663277, 0.034258767397897946, 0.04684133677805919, 0.06377856156779174, 0.08156690358406626, 0.09825574425607536, 0.11733758072332266, 0.14449663231692353, 0.18014212716965497, 0.2197614282568725, 0.2560893237156275, 0.2851210122048912, 0.30920490835549314, 0.3341991202944086, 0.3635766629760484, 0.39424006796513394, 0.41898590995138196, 0.42935194076352656, 0.4213944903026805, 0.3960398457084189, 0.3557689605285917, 0.306771515004272, 0.25866767743908725, 0.21455301784392336, 0.17057902411746548, 0.12964599895067305, 0.10054921336887998, 0.08509636501687327, 0.08173534414862176, 0.09114475100715515, 0.11361373417176773, 0.1436656792376954, 0.16842270135367454, 0.17600794844089637, 0.1655043580213595, 0.14587544256938423, 0.12604942575933967, 0.10866221020903608, 0.09262810410732054, 0.07775017114279797, 0.06477455419021344, 0.05297961787444163, 0.039392464571378086, 0.021450550187885834, 0.014432824469917756, 0.03103127199713078, 0.044670327103820115, 0.051118306426199474, 0.058313391563027624, 0.07535010104436102, 0.10087885732619885, 0.1302091704721758, 0.16121922536513494, 0.19580885462492928, 0.23963230514748865, 0.29769905133695057, 0.3688737264422402, 0.44384559184331107, 0.5106504326605328, 0.5651516050534273, 0.6124297990442311, 0.6626866601863568, 0.7211941064183324, 0.7827957123689088, 0.8337240367453137, 0.8569976155040284, 0.8425055544820889, 0.7930227693728252, 0.717880652284158, 0.6283482724201102, 0.5390473996121528, 0.4573702140966943, 0.3798225476120571, 0.3069748350492629, 0.24813699960129934, 0.2086025393041703, 0.19054454387925693, 0.19590624996446698, 0.2226800823275253, 0.26248858309657164, 0.2995480567257664, 0.3161983526897639, 0.3065660377985985, 0.28040581337657455, 0.25055542276916226, 0.22225751520339393, 0.1946004785961522, 0.16626838723176535, 0.13782575117581514, 0.10979127459608436, 0.07944308613896545, 0.04269812293704475, 0.02150826470110013, 0.04516256333213379, 0.06360035689653584, 0.07573126898350668, 0.0934142478665728, 0.12265323613610032, 0.1582316494378278, 0.1960179438198951, 0.23924823170249326, 0.2956604761036165, 0.3701097891648245, 0.46293421026954573, 0.5680179155021103, 0.6698995933539068, 0.7565357889289192, 0.8287426147171311, 0.8955101657753658, 0.968773680529262, 1.0527672077767292, 1.1411730932262731, 1.2147724948135834, 1.2496574269501117, 1.2286517211354124, 1.1560674845379002, 1.053622809486851, 0.940256223297298, 0.8291550359962652, 0.7276109938766113, 0.6338135130795304, 0.542850602063195, 0.45776321053984675, 0.38770811166960517, 0.3413165512001781, 0.32309349469687215, 0.3301639936928437, 0.3550686838534696, 0.3871941539736309, 0.4108695636726765, 0.41375850370078976, 0.39645583103655624, 0.3683911663088858, 0.337037646740507, 0.3031342616047077, 0.26421971969671676, 0.21988850994631967, 0.17253889437768125, 0.12227644735645721, 0.06498305838329932, 0.028887192380432122, 0.0594370231118243, 0.0840697737851871, 0.10511942672299304, 0.1335959973038204, 0.1711637160905979, 0.21370502999373245, 0.26093975742342257, 0.3207110654300206, 0.40257343259856887, 0.5090317846165501, 0.6353903053514257, 0.7665775490767027, 0.8823059883259995, 0.9760090001670512, 1.0556496241316882, 1.1340693896443383, 1.2223143911535375, 1.3213985353623643, 1.4228909459401897, 1.5029445601999691, 1.5356033326627596, 1.5045998526632962, 1.4160024425650806, 1.3011716936762354, 1.1869731012626337, 1.0803625043982248, 0.9823327032291691, 0.8910920821343122, 0.7985364414434318, 0.7001991208638215, 0.6056339150138613, 0.5277054092539666, 0.4736869794127061, 0.44519532904481196, 0.440114726873128, 0.45348116754255363, 0.47510848394960387, 0.4909643805762027, 0.4905447016368727, 0.47290201456084285, 0.4433017614888372, 0.40547117234991414, 0.3592906775715199, 0.3034238271874228, 0.23905572951724285, 0.1681164896643823, 0.08850477057251774, 0.0391748299178757, 0.07625965898006719, 0.10816044563884812, 0.14028701833874557, 0.17828569634927668, 0.22205988380900565, 0.2720637251029265, 0.33227417062269576, 0.41200305598933257, 0.5186026233325053, 0.6526425294601634, 0.8029964436697783, 0.945290388740284, 1.0599049932827371, 1.1490439733466307, 1.2259090323641566, 1.3043917619385703, 1.3916974841186895, 1.4852890649288706, 1.5722923689511383, 1.6275456324328308, 1.631660016362128, 1.5851065091308831, 1.4993400709950013, 1.40208165016838, 1.3169270453137463, 1.2400383895434688, 1.1636004468170644, 1.0872856546739214, 1.00656423095385, 0.9135319135705966, 0.8130101961359727, 0.7177715873404059, 0.6359779948122758, 0.5749860204256584, 0.5394772857490141, 0.5274887427094087, 0.5331652113053649, 0.5480541701663012, 0.5594876457879944, 0.5553260435409116, 0.531456507212767, 0.49163635930552146, 0.4408809003915226, 0.378961820125746, 0.3032568192947459, 0.21409080564879163, 0.11210439809304444, 0.05241183839609032, 0.09680778178155575, 0.13759274291230267, 0.18264930482653965, 0.2312932950918264, 0.28290545956098523, 0.3423212562875388, 0.41699715192760106, 0.5142116265895446, 0.638909208901221, 0.7906357622406956, 0.951021103005089, 1.0897572172380756, 1.1916385572226322, 1.267772648637303, 1.3335301802815285, 1.3982900034199015, 1.4608008324787327, 1.51736038037577, 1.5554500260993807, 1.5559749395286757, 1.5139270538790035, 1.4519182847778522, 1.3895301655660812, 1.34127818867364, 1.3138680006532801, 1.288803787688056, 1.2456779536569151, 1.185682598274862, 1.1152932417090058, 1.034399948901627, 0.9454751476570349, 0.857850840128026, 0.7765291280505762, 0.7078950972768878, 0.6580472533086138, 0.6249810861925448, 0.6048586642697235, 0.5985824575664327, 0.603961797089725, 0.6073014008428659, 0.5937604159181038, 0.5591001275728371, 0.5078263614567026, 0.4425800766375915, 0.3599003514586622, 0.25685131375160575, 0.1347644378501691, 0.06592512433693179, 0.12049738154131893, 0.173257706152378, 0.2329347322826044, 0.2946181588970854, 0.3568158708033918, 0.42714283737650066, 0.513523547232455, 0.6195843577225761, 0.7516340932312024, 0.909711108144082, 1.0699947780497545, 1.197047304125172, 1.2795510232565428, 1.336423378219139, 1.3835827693966838, 1.4218385653527696, 1.4368521882325453, 1.4285423746144483, 1.3998651149837913, 1.3424888906203525, 1.263379376775983, 1.1970230551870835, 1.1688207420224253, 1.1798802490017934, 1.2185096902114927, 1.2544562529911545, 1.2505475801098076, 1.2001874855091785, 1.122205072959333, 1.0372694442315515, 0.9594344419649771, 0.8968650094873926, 0.8468741075864517, 0.8045095604487398, 0.7681456955287161, 0.7322605984357442, 0.6930376166451467, 0.6569407818557574, 0.6370708419488456, 0.6329282629743518, 0.6279855729333698, 0.6067129434178287, 0.5628215333715353, 0.49669808658615977, 0.4080784274289902, 0.2941881819248078, 0.1553213903994518, 0.07808189472391748, 0.14479023487529175, 0.2110830863283754, 0.285387416899926, 0.3614874528478683, 0.4367526299794194, 0.5173582288320604, 0.6076767793837704, 0.7113245688435471, 0.8405295936792196, 0.9973829252921148, 1.1541175206807905, 1.2685947370759856, 1.32994757274926, 1.3595409524101578, 1.3770376136889038, 1.3804911346572524, 1.3422511614847898, 1.2650758511203268, 1.175070095814568, 1.0796656201346932, 0.9910009133785191, 0.9395374293183174, 0.948565500081672, 1.0089352501277347, 1.0975518128365445, 1.1807292992925018, 1.2109060910184877, 1.1638270830915562, 1.062537941058248, 0.9497586483957055, 0.8642356542255688, 0.8232197879543441, 0.8170621688063714, 0.8235258110098876, 0.8259206759795731, 0.8120433191594943, 0.7770696101726848, 0.7255896876326964, 0.6770792821744857, 0.6509836174642516, 0.6426005795878931, 0.6326767899794304, 0.6030043759421411, 0.5422771151898249, 0.4487083831733067, 0.32439792254966604, 0.17174639512441517, 0.08793406043393062, 0.16515097107014107, 0.24207018699706007, 0.32827962775164615, 0.4191579614726725, 0.5081303087675313, 0.5936802105243745, 0.6768106176419159, 0.7679389711069504, 0.8875666407735582, 1.0396520674305467, 1.1935573572295592, 1.3021833619274719, 1.346547876008336, 1.3397121431960644, 1.3140346944629833, 1.2796678744059062, 1.2038897335013443, 1.0830829778357098, 0.9553802507349977, 0.8491623957751863, 0.7769861188875291, 0.7552343909686446, 0.7955915641480574, 0.881837456989239, 0.9864764694308417, 1.0803633959524879, 1.1235604980926444, 1.0811721012468596, 0.9654716206300699, 0.8232505941805793, 0.712481351460229, 0.6724408424698193, 0.6986594878002966, 0.7556156872288744, 0.8085196241091678, 0.8347803066300303, 0.8269834002971226, 0.7861726631342174, 0.725871403160662, 0.6768108756628481, 0.6530754799803088, 0.6421952260311982, 0.6236726012225636, 0.5745371916855245, 0.48107211918986215, 0.3470204604612881, 0.18262957043226, 0.09411159838821286, 0.1756699089803913, 0.25623347598272184, 0.35131847180086434, 0.4571500985921082, 0.5567950565579571, 0.638324505975488, 0.7041770566594043, 0.7764978832530562, 0.8823864061143042, 1.0241377695508087, 1.1721816230732558, 1.281988918577435, 1.3201874693098534, 1.2817094729040996, 1.2126373523530556, 1.1451900411114706, 1.0554526736462662, 0.9292304023394846, 0.8010531273684225, 0.7120157270147044, 0.670202576829544, 0.6774882841848034, 0.7284373091162851, 0.8011811358823443, 0.875468441471155, 0.9373976953858091, 0.9665732239722233, 0.93510884864848, 0.8351168866532092, 0.6917858695369198, 0.558623616189547, 0.4973269886998388, 0.5287310119271604, 0.6204938135738816, 0.7220427463008504, 0.7959407507711225, 0.8272490688373966, 0.8157791134962354, 0.7675916752906167, 0.7101922753458557, 0.6711070516251787, 0.6498396508887772, 0.6315733438779491, 0.5916575675436438, 0.5033980948714829, 0.36335987085845717, 0.18932657450180232, 0.09442166406382835, 0.17165750494551327, 0.25032958402906375, 0.3540554395300044, 0.4725780659972054, 0.5757421060590628, 0.6462839284861978, 0.6923599686278118, 0.7456178326697447, 0.8324731305960479, 0.9506634929051881, 1.0782190851450382, 1.1841173243857568, 1.230308691880194, 1.1886667567584983, 1.0992079632060512, 1.0123321905040221, 0.9224790670040346, 0.8156075871702984, 0.7193356732522588, 0.6691959878646015, 0.6647860879379449, 0.6909820510773764, 0.7241015731822977, 0.7397156632793873, 0.7424305947546683, 0.749129296212796, 0.7550949780425726, 0.7405357854558563, 0.6799024829984319, 0.565562125562579, 0.4294866608125911, 0.3390722372020565, 0.34674417123166223, 0.44589823549550694, 0.5819120607746332, 0.7014615801960304, 0.7770782177482078, 0.805050769065936, 0.7881268808780687, 0.7436271272823947, 0.7011243930914303, 0.6705603729428009, 0.644481126607102, 0.6040737758172094, 0.518868529969746, 0.3761303200723833, 0.19495680162977927, 0.08642357778209912, 0.15513834378957825, 0.2329171051917569, 0.34404234797891964, 0.4673655686583803, 0.567491126295934, 0.6298826941275479, 0.6656744320934632, 0.7044728581344312, 0.7651195628273203, 0.8443580092446337, 0.9310593394194742, 1.0147941511335357, 1.0706950492588192, 1.0554000461119504, 0.9794444529212181, 0.8891749876588769, 0.7977726669328132, 0.7083393238159583, 0.6487446126929014, 0.6395722262644336, 0.6709108760102609, 0.7074785513672621, 0.705672837870781, 0.644893154551765, 0.5688797052758718, 0.5277341293251318, 0.5248127567852755, 0.5374260495875638, 0.5241523199311479, 0.4490121666099349, 0.3246689670154795, 0.21211060039711707, 0.18134834664930008, 0.2597700734453696, 0.40680840740374424, 0.5595311263559849, 0.6782497946550139, 0.7522294736660724, 0.7807201026479919, 0.7694794452042429, 0.7416918524805687, 0.7120911887276742, 0.6777311746936462, 0.6276668123416559, 0.5376580524506639, 0.39081263939529026, 0.20263781392739516, 0.07157422458072914, 0.13353643655196942, 0.21358834684303654, 0.326848732779381, 0.4470135466128601, 0.5460978045454999, 0.6156037940108118, 0.6583291303350978, 0.6876475110321071, 0.7169062826569799, 0.7489143245836335, 0.782038529687369, 0.8241343001838906, 0.8699759541765014, 0.8800268296086348, 0.8364247794882733, 0.7546227856094307, 0.6549007400364653, 0.5614769314411107, 0.5090853858299581, 0.5129525067245928, 0.5556071678513829, 0.5916799134985525, 0.5597524576553305, 0.4424874963361898, 0.3202753816377802, 0.2611350199045618, 0.27108434779634744, 0.3230245417241148, 0.36354896905732803, 0.33194751764705915, 0.22382074179389114, 0.09856099952810118, 0.03424299148240471, 0.07903078665067488, 0.21604767654721313, 0.385579405756068, 0.5397590640422564, 0.6603761544143759, 0.7425202235594661, 0.7806591346245487, 0.7862433914740891, 0.7730442035364847, 0.737228020971366, 0.6730229803079042, 0.5695207080326158, 0.41343140660294636, 0.2150824326873778, 0.05421540773269592, 0.11181070633429177, 0.19408477793904694, 0.3043984815985692, 0.420815562643215, 0.530401034869247, 0.6272729920917421, 0.6932652973531803, 0.7201030996495993, 0.7213283749299543, 0.7077843248235899, 0.6847530265112564, 0.6719297939994351, 0.6838344706576569, 0.6935516678258904, 0.66789612363416, 0.593816534064271, 0.4820361647873613, 0.3624024072791845, 0.27835711027984295, 0.251210974604628, 0.2623119327482132, 0.27525181241671065, 0.2295038324668612, 0.09848657605821982, -0.02958673765516306, -0.07813027571109195, -0.0426181726695816, 0.05298197069111977, 0.1546642586504798, 0.17883906246815004, 0.09442597249109229, -0.03663732094943436, -0.12086212864403728, -0.10259846668924011, 0.017150091517620362, 0.19339443751136595, 0.3772823803584684, 0.5425739743848162, 0.6802237181499439, 0.7766416833297433, 0.8290375192823465, 0.8454041886187823, 0.818076378287839, 0.7414519149620478, 0.6185265505756148, 0.4464735714380679, 0.23287373573992795, 0.03769040156901786, 0.09108841259191149, 0.17258475229872217, 0.2780766116643341, 0.39683747528060376, 0.5298694802668792, 0.6679121437542117, 0.7702284802114966, 0.8090234051854641, 0.7939131263392256, 0.739847132064647, 0.6630918209177478, 0.5961895150009259, 0.5659907941778837, 0.5501744855372926, 0.5098976919900002, 0.4258320111617323, 0.29603213481902096, 0.1439962794471939, 0.015426785290587356, -0.06333946807157319, -0.10520811879716167, -0.13482709292566306, -0.1966085515183373, -0.31953242082514205, -0.43281067222805975, -0.4594198411204153, -0.3955500589727299, -0.2602910369238476, -0.10323999070450283, -0.019585346627395063, -0.06678397171652188, -0.1942940118008222, -0.2935375912048952, -0.2952954656759652, -0.1913824859343886, -0.011791408251018938, 0.20103625176513132, 0.4121702396918492, 0.6060934640973773, 0.7645146653703008, 0.8702939459799, 0.9221195453448392, 0.9093608142317061, 0.8247494352049773, 0.6813320844076944, 0.4885518346498676, 0.2548699712326381, 0.02458147210110034, 0.07219034360372507, 0.14894351229560618, 0.25088080402355367, 0.377388342381955, 0.5353981127383393, 0.7140380976248525, 0.8602389417261951, 0.9254504476893625, 0.9018405361480513, 0.8084990674005454, 0.6877043884886244, 0.5874763116760863, 0.528785409230195, 0.48251725445098675, 0.4096898679799353, 0.2984093128014248, 0.14661861175053617, -0.029484948299154396, -0.1952691516818363, -0.31995099085695217, -0.40850056628491954, -0.4815767523202871, -0.5629155906514381, -0.6723672759957704, -0.7665278126786415, -0.7763750845954481, -0.6878047042443284, -0.5193822601612971, -0.32615821280964047, -0.20186092117287902, -0.2098673390133675, -0.32150974612293154, -0.4362355546798724, -0.4690600027420218, -0.39233778879578934, -0.21949604015251895, 0.017365316891699248, 0.2752598283835378, 0.526931193778576, 0.7496110894676463, 0.9119339147298914, 0.9999197343607619, 1.0025553725404535, 0.9128025054171, 0.7500436202532661, 0.5351292752643451, 0.27919963342389253, 0.01668107337358237, 0.05805894756724527, 0.12828772511256595, 0.2268733353048357, 0.35702652173432087, 0.5270875298091783, 0.7305231504954688, 0.9096523279552732, 0.9939741088380731, 0.9562045652905946, 0.8286164195851144, 0.6842939355641597, 0.5816654465056786, 0.5244144416466423, 0.4669807191599084, 0.3707193380021158, 0.23463803666380478, 0.07149254271861792, -0.11440576002189246, -0.30599906018709827, -0.4584963556904392, -0.5717020085712898, -0.6663824101821665, -0.7492436813505468, -0.8410739339099125, -0.9211747591544878, -0.928282900758375, -0.8274200554951837, -0.6345564190062273, -0.42226234130345386, -0.2828182600562915, -0.27020444584443437, -0.3689849364123777, -0.4980970304675973, -0.5720844002775551, -0.54372847252156, -0.401212403619789, -0.1592516295652773, 0.13645516827860116, 0.4435825955124973, 0.7306696754112008, 0.9512850987820477, 1.0750469325420595, 1.091169996379502, 0.9968702865780786, 0.8162834042361492, 0.5798763491712207, 0.30248802550973486, 0.015451294976972056, 0.052729724819528326, 0.11491532174983726, 0.20581397745025165, 0.33014083331235816, 0.4933398680692876, 0.6913009764812367, 0.8669146191863705, 0.938906443908341, 0.8777181399894228, 0.7328124841367752, 0.5907116554580428, 0.5089662242741404, 0.4734883399719531, 0.4282245959115313, 0.33545084725340785, 0.20007940527393994, 0.053084615936201576, -0.11293724534965797, -0.29617606748055497, -0.44504855091445866, -0.5605261769546307, -0.6547536362139378, -0.7232059134758252, -0.7951413196980298, -0.8678856763844499, -0.882668441965241, -0.7837331371252331, -0.5806476232991237, -0.35987988485003763, -0.22102250125301445, -0.21063678266384064, -0.31894106085819446, -0.47526601258732165, -0.5931592028492857, -0.6211481635808376, -0.5289565886055876, -0.30801886625556824, 0.004263377423339819, 0.35482313763802653, 0.7001920394092065, 0.9773331519533343, 1.1366316002045873, 1.1651641146582428, 1.0661191732836512, 0.8693756739632061, 0.6144272325767303, 0.3200714437512785, 0.021135502645448646, 0.05668078723923571, 0.1085639562700388, 0.18667138792702764, 0.2971280685790435, 0.4372402768317044, 0.5976123252547011, 0.72646065188815, 0.7546791767900465, 0.6672739458541657, 0.521333538617686, 0.40000379159596955, 0.34517499240499877, 0.33206156051940355, 0.3153604994177436, 0.25527499641359175, 0.1544409669950372, 0.05395239767195917, -0.0503092139128224, -0.17435378699519666, -0.2847397394318616, -0.37443102295304015, -0.4466973055466813, -0.5025064166354396, -0.5618333616481884, -0.6342376335768138, -0.6659087679512401, -0.5835440136245947, -0.3895969675657066, -0.17631896074450384, -0.05262143180793329, -0.0609900257247539, -0.19163996291958074, -0.38851894736169346, -0.5553107370724025, -0.6359642709091071, -0.5984971480053988, -0.4184881881923161, -0.11521446895343032, 0.25812933655162984, 0.6463324929301081, 0.9713310614941215, 1.1650330630152252, 1.2081192098691158, 1.107439017639325, 0.8986392373929839, 0.6307747352667458, 0.3274790863439058, 0.031077176326085188, 0.06744355780592293, 0.10830313619629302, 0.16911814618819576, 0.2608618597468034, 0.3721737660652806, 0.4790807465873552, 0.5356299376929623, 0.5023295684913427, 0.3884786310596397, 0.24935720260911892, 0.15145154099054614, 0.11778085638179528, 0.12644003948104046, 0.147124743975754, 0.13336491500942485, 0.07744150620658918, 0.02722317845597929, -0.0028554326413236008, -0.04286881132187788, -0.07803736085514515, -0.08952089154162991, -0.10106871866246524, -0.13276793481557553, -0.18993258635518137, -0.27435380296133405, -0.33657696483761707, -0.29870596348899187, -0.1479641967525628, 0.02811530620765053, 0.11867277086705731, 0.08470441996709555, -0.05832218279955758, -0.28191376665686635, -0.4927954693386755, -0.6199744418957898, -0.6310138981607157, -0.4975319045629466, -0.22254766463994274, 0.15055524930704625, 0.5596220744615665, 0.9161005893319476, 1.140212149604562, 1.2027451031105696, 1.1080920886323835, 0.8957385532209897, 0.6239755557648786, 0.32224897075499215, 0.04160303213245424, 0.08013273224785566, 0.11079468464315104, 0.1538078021005808, 0.22721469871822791, 0.31188411679419037, 0.368066595177633, 0.3551747013414801, 0.2633058903035922, 0.12700022374793207, -0.0068775462898381864, -0.09541033316292274, -0.1187532640923688, -0.08787965421876824, -0.0294311591346333, -0.002197026449277872, -0.028646751151671535, -0.053669287164799934, -0.04316980796212087, -0.012538701998766133, 0.05185976232412962, 0.15046251615349263, 0.2327360024035678, 0.2623193108912749, 0.2203408396290169, 0.11776320645317814, 0.018591905832012954, -0.0067781741588478816, 0.06281072818658659, 0.162766560341503, 0.2014172297539626, 0.14650740410535865, 0.01183393319626859, -0.20898441042096036, -0.4468683145992632, -0.6131247324540164, -0.66303321425524, -0.5667732132999089, -0.3224698277186135, 0.03396901468739044, 0.44070468513472966, 0.8076063741599968, 1.0525897124536359, 1.1376486856892853, 1.05859848433363, 0.8543712989110229, 0.5904870773061509, 0.3028503934144161, 0.048685439857156364, 0.08898599769143997, 0.11276475727290168, 0.1419263938736237, 0.20018266268518745, 0.2646998134554723, 0.2845834041715552, 0.22357665463971385, 0.0919206279423694, -0.060178012343678276, -0.19260991226792273, -0.2795314163312707, -0.2966836258351205, -0.24750777236332405, -0.1651367762984842, -0.11521416158323199, -0.12884522903506251, -0.1481064535473218, -0.12029991321722536, -0.04388235054032232, 0.10024275446043777, 0.28883895880638416, 0.44036612196278674, 0.4898602751112333, 0.4503139241908563, 0.36479101440901546, 0.2678542628398529, 0.21266590831051324, 0.2159341673367784, 0.231624781319349, 0.21143570001963194, 0.13761920614538617, 0.014094428887436814, -0.19288214956700686, -0.445913026125938, -0.6453013329607842, -0.7246997963299658, -0.6502125178309379, -0.42526054730352386, -0.08862823711738728, 0.2999941023038902, 0.6576095790844219, 0.9089971681428399, 1.0131778678747339, 0.9563117186692461, 0.7722474931071531, 0.5293585310947758, 0.2691059727296685, 0.051384184241329595, 0.09224829245427678, 0.11304980577217179, 0.13524821041808166, 0.1850864978159918, 0.23749924308448606, 0.23564366548482008, 0.14843224753677353, -0.004383962602173415, -0.16561866044265844, -0.29170989856073454, -0.36682712652590227, -0.3715606455216919, -0.31155819210757757, -0.22842019209224315, -0.17818980278461466, -0.18634063649375013, -0.19457113688021074, -0.1431475587323422, -0.03385272664608907, 0.12097146875394733, 0.27360407518976315, 0.34671521987662623, 0.3058847919125198, 0.23625019424862015, 0.2094518430306457, 0.2170281716322968, 0.25074831638103723, 0.2857898579575852, 0.2760402172219539, 0.21885932512653955, 0.12034910071980831, -0.015073851669352796, -0.22445430713083067, -0.49371242711441343, -0.724792176812919, -0.8289734623891699, -0.7635829978211993, -0.5431744650618361, -0.21917629735511046, 0.14815748020869204, 0.48519931858716964, 0.7285480198055614, 0.8426478910086939, 0.8090786857848857, 0.6540762095159083, 0.4440259628706307, 0.22329831956563698, 0.05201050797292798, 0.0922833255049301, 0.11408026522460907, 0.13845504703697725, 0.18822243805749617, 0.23558054528511355, 0.22313897630922713, 0.12467796633276158, -0.0363124981707133, -0.20154393249439415, -0.3198647764768433, -0.37420378282408706, -0.3577042341804591, -0.28764240578312356, -0.21017068929380917, -0.17140755375706251, -0.17161775425935172, -0.1451054958545283, -0.055933173768887304, 0.06381991364768662, 0.14929278752342015, 0.15461025641865248, 0.05930729048319607, -0.08431490306542196, -0.18537260229377892, -0.19210474355055698, -0.091126051473889, 0.09094769064927166, 0.26626971779066055, 0.31736030883430594, 0.25350746206908337, 0.12303603992291377, -0.05509181164954624, -0.2929987240459017, -0.5815988468340273, -0.841412322612209, -0.970884724563181, -0.9112878964470466, -0.685834260723179, -0.36338594112442807, -0.010344405533343709, 0.3048027140740791, 0.5307045479095664, 0.6441152985757831, 0.6298374494891078, 0.5080916352037848, 0.33995406374204035, 0.16860472115485273, 0.05439671864394901, 0.09431028445748177, 0.11879089835106665, 0.15124548093544912, 0.2097760549301807, 0.2608353799512184, 0.24563751390001695, 0.14411481022984252, -0.016913925250876958, -0.18205509813356435, -0.29411013848519085, -0.3286826165769965, -0.28675111928382635, -0.20006528717254524, -0.12400108625301293, -0.09582689885044111, -0.07917516931273948, -0.003866222607002805, 0.13168502879277216, 0.24611958304872755, 0.2078997343442294, 0.04028495135142799, -0.1756704483907843, -0.3969459354987486, -0.5408072119338688, -0.5463056168094161, -0.40141738462670457, -0.118105029967957, 0.21068146086698414, 0.3755426730749698, 0.3151745337963639, 0.13836390044161545, -0.10504724778243585, -0.39167445086935604, -0.7011596854810622, -0.9829323886852613, -1.1363390973255396, -1.0850327770158767, -0.8536044235852898, -0.524673175028552, -0.17551129959374587, 0.12276195407777772, 0.3280668241984667, 0.4332250579149989, 0.4322718635381986, 0.34368650328399736, 0.22305960326579902, 0.10821841038111525, 0.06178271307288848, 0.10277512389431821, 0.1293839090634548, 0.17054538801078614, 0.24067340504558013, 0.30081854941393044, 0.2899510623262152, 0.19132815177233906, 0.036264470239584186, -0.12058504080763421, -0.22282988155633046, -0.24365160330640676, -0.18552512441718597, -0.08710276123000842, -0.006575526637234296, 0.022412648865779525, 0.045263365364481424, 0.14019007342813944, 0.3086771770412408, 0.4256150200386239, 0.27414189064739797, -0.00742831674137122, -0.2787850083463834, -0.5306192598757017, -0.6964573110468343, -0.7108490259739404, -0.5704773102738825, -0.25085062273036646, 0.17364708053724537, 0.4434613003357724, 0.37527351817742755, 0.13871953591606448, -0.1708470394415909, -0.5083575893676803, -0.8399819245886245, -1.1384141511169923, -1.3102616399812226, -1.2678944972447883, -1.0337544146575028, -0.6967957618765108, -0.3453992336508129, -0.05851417800948782, 0.12794287247903938, 0.22229009516092582, 0.23016911260137787, 0.17291512185781457, 0.10193209354615784, 0.04648399153684146, 0.07418299920302764, 0.1190844151294801, 0.14628236052062246, 0.19068860714104857, 0.267893145280448, 0.3372581025237761, 0.33280136971011426, 0.23959842665128356, 0.0963514220433325, -0.04257937988197899, -0.12584003394073096, -0.13172264662963268, -0.06760399777841362, 0.03046306217677145, 0.10473304482834164, 0.11778234314141572, 0.11845042753945728, 0.197316175867519, 0.37456061567976395, 0.5140881618293264, 0.3295958970440168, 0.02003441668944799, -0.24472146930356495, -0.48447046069425587, -0.6511256165807126, -0.6920479930020444, -0.5878179591530146, -0.28057762000331754, 0.15365189465526669, 0.46477346410731624, 0.38449394895081784, 0.09634558315345808, -0.26000158179072225, -0.6336744564526162, -0.9858065730159421, -1.29495350596717, -1.4733370805392414, -1.4363454628300532, -1.205210187907447, -0.8663507748640923, -0.5149507235993762, -0.23786461675641754, -0.06703511468192586, 0.01778817678355907, 0.033238397916135816, 0.006210149191466668, -0.01525518314313442, -0.012414957762169863, 0.08619198995802303, 0.13666892673682252, 0.1650121282619636, 0.20655975976907837, 0.2789996264496017, 0.3494275772777645, 0.35072948759865236, 0.2639189523819364, 0.13539753295507148, 0.024031245650392812, -0.02689208952505831, -0.008136290964808475, 0.058574942918491864, 0.13764372394931962, 0.17792178903079325, 0.14556026536013705, 0.09572257855046629, 0.1360809026347283, 0.3023396156106483, 0.4626426476716007, 0.3411368366691661, 0.07361912178260005, -0.14018049282541992, -0.3203865407135638, -0.46609303132118396, -0.5401935925186853, -0.48618242909872517, -0.22953834724798639, 0.1454183347003815, 0.41715978901245004, 0.31653215275668445, 0.0007359464635001882, -0.37475225239951077, -0.7606896193956408, -1.1217433291612873, -1.4322636898393626, -1.6048670244828571, -1.5687974211394151, -1.3472816778963732, -1.01760093208902, -0.6753703343383718, -0.41163487830311585, -0.25508201573706635, -0.17770625171357876, -0.15369112478315103, -0.1503716928955276, -0.12397984236280879, -0.06661571093120032, 0.09094929912353515, 0.14527525679060596, 0.17629801913727203, 0.21207612616361723, 0.2679179716456579, 0.3256456902339769, 0.32802978039946495, 0.24992079905226464, 0.13788636160890003, 0.05737704357101913, 0.04760835870549021, 0.10703450306428063, 0.19040811015597123, 0.24629715508086533, 0.232623354911037, 0.13013074896635232, -0.0022228223513209786, -0.04694010099517897, 0.06082185085673055, 0.21533762766051465, 0.18673240379951983, 0.03945580294875403, -0.06871519837546464, -0.1499831953361791, -0.2407655202448797, -0.31830033058021306, -0.30348659250792653, -0.1129943746571791, 0.16915424400932128, 0.3423343687672981, 0.20639902182716854, -0.1146811358281299, -0.48751332854952156, -0.8656010303455957, -1.2241711777180868, -1.525746307404042, -1.6828519709397223, -1.647884640669006, -1.4444706460211778, -1.1358802997705446, -0.814456416228998, -0.5708455508128674, -0.4296544791155203, -0.3581809163347614, -0.32397635853121487, -0.29081455622820757, -0.22072060361711057, -0.11503248027033262, 0.08648584666859843, 0.13990293092847317, 0.17301517240228892, 0.2034822635050828, 0.23817512967273996, 0.2717185700400968, 0.2673238296566445, 0.19997007857605595, 0.1058626690648912, 0.052698914928831955, 0.08163211977416532, 0.18646127739275573, 0.3062414727054413, 0.3568634227308657, 0.2883476458091534, 0.11200216909510653, -0.10185729792976392, -0.24786929540424635, -0.2477982102619598, -0.14584723544402203, -0.09371948184778854, -0.09454375765643544, -0.06946155133692, -0.03704068606144963, -0.04699796341251317, -0.08543382785463097, -0.08473914631355085, 0.036304404570915334, 0.21559686538383901, 0.2790821753255744, 0.10786574354781063, -0.2056951782785625, -0.5601751375805686, -0.9177976013554014, -1.2662342614021935, -1.5530293026762032, -1.6956429948515603, -1.667138853654969, -1.4874260776449548, -1.2087915158201783, -0.9196155680604917, -0.7043452854712579, -0.5810843273021536, -0.5145344523266234, -0.4689307731597571, -0.4078270431429915, -0.30061722168219335, -0.15541701853365272, 0.0760725992825777, 0.12440317178848917, 0.15619594739909118, 0.1804732211458227, 0.19647111849678478, 0.2056771276550829, 0.18906093831752444, 0.1301245457849499, 0.0553179495286858, 0.02259624607742262, 0.07499921791616031, 0.20882983808687702, 0.3618328324238314, 0.42760056835680454, 0.3281236658290537, 0.09031614025016035, -0.18731135468632315, -0.4055256868863167, -0.4984817596851938, -0.46300194558589575, -0.37049442514073344, -0.26117706804974045, -0.12553448598279376, -0.0032748731723839875, 0.06716966413833064, 0.09094558592493443, 0.09822563117714012, 0.15846040960995214, 0.24142209582425322, 0.2249867559771903, 0.040519820887250375, -0.24925650233128552, -0.571919951742787, -0.905696502003329, -1.2420534104321381, -1.5123961187062012, -1.6443330069058175, -1.6259872792733627, -1.4724752985874725, -1.2296216199190142, -0.9810098588479097, -0.8003817091369737, -0.6976827688799704, -0.6362675378301094, -0.5796019867187139, -0.4941063435298682, -0.3580038850445556, -0.18434262153367545, 0.06496687938370817, 0.10647468401381525, 0.1332095946034372, 0.1493925166372989, 0.14966906166762994, 0.13899637768112758, 0.11042476144215145, 0.05590734475185427, -0.001836876443175125, -0.018038838851305136, 0.04147890823548216, 0.17316277891390397, 0.3231965757903936, 0.39144724213559684, 0.29017446438877903, 0.035087988007043866, -0.27186474505599706, -0.5283119369691552, -0.6761720377354934, -0.6918829434652237, -0.5953097411086848, -0.42205814451917045, -0.209981464859601, -0.0262209019983451, 0.10188681961665688, 0.1701131081514503, 0.18374368944346645, 0.2016887507362382, 0.22483726020413808, 0.18007136477124022, 0.014786623687697625, -0.23583466879494835, -0.5254236784620874, -0.8399803316385603, -1.1602695980864026, -1.4112038762411527, -1.536847640565984, -1.5315949332352214, -1.4037562355800726, -1.1968670316965482, -0.9904430301735216, -0.8463588019298582, -0.7657911960785102, -0.7107394246392237, -0.6455277452844038, -0.5419262833677918, -0.3875464542020051, -0.19881757993632376, 0.055957703401682296, 0.09339670195803658, 0.11451081241355941, 0.12030634986967158, 0.10671192291962701, 0.08054350078995283, 0.04070583258328724, -0.014260700690573239, -0.06163513419957128, -0.06844754730446827, -0.014913128931069686, 0.09016004763683141, 0.20285103631636733, 0.24611258388378462, 0.15268930309009426, -0.07526724632200851, -0.3641751743281558, -0.621154509908587, -0.7853805569779108, -0.8240596152710332, -0.7334242696894099, -0.5320639405871007, -0.27384096712456674, -0.049968328248115576, 0.097103799157686, 0.16381461534432576, 0.17342352603344122, 0.1808753230640368, 0.19247644958949578, 0.15720101664085503, 0.03364486977382265, -0.17176237801103023, -0.4323836557878321, -0.7307789125533642, -1.0324725477391714, -1.265294422334882, -1.388427364996085, -1.3951436682918161, -1.288413201944469, -1.1138319328232984, -0.9476451200276671, -0.8393482370570002, -0.7805934112308685, -0.7323409913938423, -0.662397328302374, -0.5496736439720846, -0.38947485747767085, -0.19927561425221882, 0.047882690468777925, 0.08577940366302488, 0.10608818678051533, 0.10351021377874015, 0.07793893813230206, 0.0403100142080978, -0.00796201522698868, -0.06791279167305093, -0.11475382794468661, -0.12067756153139918, -0.08175068177077133, -0.017466754391993557, 0.04068973694018152, 0.045210014805515064, -0.04404712372420289, -0.22752962172688965, -0.4672579256275421, -0.6927104942679847, -0.8408861277284723, -0.8741367388824223, -0.7828165506173999, -0.5782379263354843, -0.3090933690023397, -0.07616370936143085, 0.05741713303299034, 0.10338769833305071, 0.11543558939746267, 0.1375203030501147, 0.16334676587981278, 0.15588023252329303, 0.08049410288655114, -0.08100040405027013, -0.3160392299572979, -0.5990176258341481, -0.8801997930133065, -1.095111296871653, -1.2138799486080176, -1.2259111816710826, -1.1344743351798314, -0.9907233327789989, -0.8647923098609099, -0.7911005474993442, -0.7517960516027328, -0.7093542383243922, -0.6385888323476544, -0.5256401111497242, -0.37034816999569514, -0.18926465879148838, 0.0394394917035164, 0.07915991560375917, 0.10365674588928396, 0.09993726411625668, 0.06961371294257039, 0.02706912064259459, -0.023788750562203538, -0.08867087853971006, -0.1456330840502294, -0.16302123819882838, -0.13915987301862162, -0.10775500045320244, -0.10270378521053192, -0.14204419652574238, -0.23803801265218175, -0.38507866482077274, -0.5695436921261108, -0.7523616598770222, -0.8734312853772553, -0.8919942968328829, -0.7989500153471801, -0.6095120586767608, -0.3609536207231597, -0.14354415373187057, -0.022237993490129022, 0.02358097683975217, 0.05087898829875857, 0.09273296044579687, 0.13671908706427524, 0.15606166783772493, 0.1175343119275915, -0.007645729756680293, -0.21666836735630116, -0.4758044257293005, -0.7283113720166915, -0.9190775274692365, -1.0242608592211773, -1.0323936324385976, -0.9542930272881325, -0.8447558659901633, -0.7603114108786028, -0.7182187344265794, -0.6942934030989543, -0.6566761612657904, -0.588710379148209, -0.4818045714107471, -0.3380455669894274, -0.17260856820117937, 0.032860995832359026, 0.07210901693780082, 0.10169876286794738, 0.1047146272552462, 0.0792002916887578, 0.03927139619855457, -0.006206826490019449, -0.06809608474203273, -0.13640728557616175, -0.17893313722572698, -0.18168495052481298, -0.17117018662703917, -0.19498258731287252, -0.2672408903855634, -0.3750419801247748, -0.5002818814897283, -0.6363319113153392, -0.7752572791202951, -0.8732006220903109, -0.88701287229241, -0.8056166533031581, -0.6475192631695648, -0.4396783211806941, -0.24794207909657381, -0.12533476908746355, -0.06051005561786618, -0.0144943406832697, 0.039304305872493325, 0.090552149879886, 0.12304549850227696, 0.1058623981227445, 0.009823110570708284, -0.1665872527137933, -0.38638917200020584, -0.5954940446851275, -0.7489280097153842, -0.828904915056222, -0.8279689907100117, -0.766863412492881, -0.6956976106650087, -0.6505427090500426, -0.63385738738869, -0.6209496975870041, -0.5888054758819778, -0.5272642467123695, -0.4297702899476773, -0.30012879465804143, -0.15296463734548202, 0.03272185180786724, 0.06984393581044884, 0.10170540846806013, 0.11589124971849851, 0.10423119392297502, 0.07199248392770607, 0.033832822336199234, -0.016938257283600915, -0.08574631859736735, -0.15152452313072062, -0.19400072712119626, -0.21517895449131216, -0.2531590906714508, -0.3362777747496205, -0.44825330442017786, -0.5585529412753935, -0.6552608743886238, -0.7475061846617078, -0.8197899972651076, -0.8348043133669738, -0.7768667438940579, -0.6611200208982342, -0.5076072409854283, -0.3520707987072561, -0.2344743694758084, -0.15686560933539145, -0.09985890098918776, -0.04526671412398119, 0.0048421121587351405, 0.0413066340810278, 0.03509206571008919, -0.03832287745563277, -0.1757155090219612, -0.34061110701306235, -0.4901946039420126, -0.593181111868346, -0.6397211443063401, -0.6302599789490898, -0.5920647376512184, -0.5599812233212491, -0.5480937355093888, -0.5499220799078083, -0.5454138001469927, -0.5202257928514522, -0.46674734688000435, -0.379141696794543, -0.2636636709163838, -0.1342911453969469, 0.04061341205271331, 0.07834188159080338, 0.1110439336430747, 0.13502265408881506, 0.14047410863795237, 0.12088997093299206, 0.08795814364210358, 0.0458718820487949, -0.016405714998278118, -0.09312387285975517, -0.16876633615225953, -0.2303179288342733, -0.2881538528341969, -0.37046511560233053, -0.47570778657125523, -0.5733182820820745, -0.6416736134964369, -0.6903313606400333, -0.7285465432896627, -0.7372938947730997, -0.6986662558225952, -0.6218902671288324, -0.5243373685878061, -0.4181336168234153, -0.3277202122081954, -0.25914258123435985, -0.20559444323635268, -0.15713992908277383, -0.11067576759723971, -0.07718332084198957, -0.08073604506794033, -0.13561309178487227, -0.2280657315050375, -0.32885405512313043, -0.4098391435884059, -0.4561938988323119, -0.46899292443514734, -0.4572062319992992, -0.44555556444059546, -0.4475785463472235, -0.4610607712491113, -0.4764782837995869, -0.4791924818178728, -0.45989402560956266, -0.41206040296369245, -0.33312924357302115, -0.23163752947024427, -0.11854319669928277, 0.05319059692209448, 0.09726869952238976, 0.13333288230916707, 0.16398683196493816, 0.1825422488991245, 0.17637072970423964, 0.14715441311341743, 0.10509805693127663, 0.04476527071148565, -0.03644849653669936, -0.12897383280976812, -0.21841101197926163, -0.29601808243493133, -0.3751943279938487, -0.46521016505228213, -0.5492252372540583, -0.6007798678768532, -0.6194194730815392, -0.6246326730321138, -0.6193674973178911, -0.5903932397813556, -0.5410042857485038, -0.4868133713235043, -0.43156331314182284, -0.38218481142897803, -0.34101026968703974, -0.3040204337686708, -0.2677146391077079, -0.23159635361212247, -0.20876320815836058, -0.21272388406302573, -0.24478413922626413, -0.2882157308517815, -0.32483057017935496, -0.34073316843110785, -0.33982609187301427, -0.3307712554295513, -0.3250467621409203, -0.33651043647787726, -0.36143134942638677, -0.3913591425579014, -0.416483803599306, -0.42450550182259267, -0.4074664419653249, -0.36164208281546106, -0.2904430193211589, -0.20281511831701488, -0.10471686792999885, 0.06443858100329003, 0.12096052209730078, 0.16543720185495006, 0.19976081851454747, 0.22473486874512857, 0.22928268045053288, 0.20303396217897404, 0.1530579836139919, 0.08439221542781108, -0.004026475614951849, -0.10392911699300486, -0.2027189845251508, -0.28713974483648375, -0.3577460897071783, -0.42524843850103017, -0.4884944871770026, -0.5278169073898679, -0.5313977105815277, -0.5151781471390271, -0.49571721935067653, -0.47116478309192944, -0.4408096957507948, -0.41577346000092796, -0.3994816864633805, -0.3886608276870031, -0.38058594284535147, -0.36886556912712093, -0.35275058908221274, -0.3349181011838987, -0.3241753259800826, -0.3221596766783107, -0.3243153252978953, -0.32103948954661327, -0.30460905233543756, -0.2766700857435379, -0.25138817090608395, -0.23621711134864348, -0.23967654664405455, -0.2636216904581171, -0.2985856315547413, -0.3367263824641819, -0.36695616323156716, -0.37715262168891994, -0.35986133573728163, -0.31528992122725197, -0.2516620238747425, -0.17633042500455645, -0.09146633217002835, 0.0714148507402758, 0.14210772493593257, 0.199731083015544, 0.2367042237773688, 0.2593556193038172, 0.26773120818492535, 0.24655888476756804, 0.19016263559476138, 0.1080375774859962, 0.007546837178446885, -0.10044371407870957, -0.20105724832931351, -0.2819773444214233, -0.3383534700680166, -0.3789274889235966, -0.413358209633215, -0.4355905186189831, -0.430645813135756, -0.4032866318256747, -0.3724174295601917, -0.34739725846362257, -0.32969914252470106, -0.32424792117261353, -0.3334167531053162, -0.3516121470749606, -0.37324695966531984, -0.3894273822046187, -0.39686329458454034, -0.3973892936530589, -0.39199199932456824, -0.3770997661858416, -0.35119505217681, -0.3145490024613997, -0.26935712078608365, -0.22576648449220144, -0.1951364671773387, -0.18216340089323352, -0.1906960591044154, -0.21668879179487785, -0.253687517994529, -0.29329946244767485, -0.32270314136951894, -0.33144443960290687, -0.3137193610393826, -0.27248173910987333, -0.21661554275692024, -0.15119962899820558, -0.07790749695835095, 0.07503990180724204, 0.1538734093868815, 0.22335767142802548, 0.26614148647292785, 0.2821836073919334, 0.2817816178338406, 0.2609977021906516, 0.20645811813201712, 0.11943682237059004, 0.012001941409362116, -0.10212680583362993, -0.2047208639617884, -0.28121797667710713, -0.325968068972565, -0.3446966187502701, -0.35190506504937696, -0.3533857511760049, -0.3395606677473937, -0.3054762323654039, -0.26463583092128273, -0.23286856677626938, -0.21825983109553126, -0.22311639745118958, -0.24687862067507452, -0.28377516359230776, -0.3267400471893939, -0.3646901466212181, -0.3904185787835418, -0.4020632264602672, -0.39657002805531394, -0.3716990686696072, -0.33084703642674124, -0.2818571073834463, -0.2319488005029934, -0.189793095592401, -0.1618285096208894, -0.15238002872055728, -0.16133976538793268, -0.18486218919445166, -0.21905536971960463, -0.25340387124536906, -0.27627302225985756, -0.2806753547189648, -0.26345843365039334, -0.2281524331354609, -0.18080345702370806, -0.12484347308735984, -0.063407476328123, 0.07529747571404045, 0.15222449875266494, 0.22467752006640782, 0.27511974321779525, 0.28997913764433253, 0.2754474306937536, 0.2424966989083158, 0.1877873477480315, 0.10631198147107714, 0.00560678518926598, -0.10136258456370138, -0.1984669704562271, -0.26909833928519367, -0.3070171894395748, -0.31561142071215875, -0.30698363893481, -0.2929751661258701, -0.2710983607365754, -0.233553424042788, -0.18533028267469678, -0.14361686104219318, -0.12206487340288974, -0.12616033258340326, -0.15343708060070146, -0.1982926932950459, -0.25147737763397776, -0.3011381581919347, -0.33700096350164954, -0.35434503606226814, -0.35041018866290835, -0.32477859803128206, -0.28376642570371013, -0.23776866436293878, -0.19463452906454437, -0.15983714418927458, -0.13797982744373766, -0.1327871462939792, -0.14123557484074103, -0.16011422738721276, -0.18620238737038353, -0.21039135818561364, -0.2244291409320293, -0.22411243807049178, -0.2084879078128638, -0.18022532582470777, -0.1423746556955223, -0.09742214411740685, -0.04898734641343615, 0.07025776225784873, 0.13762793476339713, 0.20262832084584606, 0.2554494556555845, 0.2750932410826109, 0.2544995124448311, 0.20680310677822425, 0.14326319084378955, 0.06603751353433966, -0.020904989091045167, -0.10870835367415363, -0.18710688453119548, -0.24413772402817388, -0.27350486094606963, -0.2778168108562743, -0.2640246352211216, -0.2431612258489367, -0.2177186039681662, -0.1814999257401465, -0.1332892687686249, -0.08562741692790234, -0.054241779530520264, -0.049187449389184984, -0.07032622653145171, -0.11234877559963642, -0.16500202496425373, -0.2171222122640477, -0.25689476831147084, -0.27842789636422, -0.27903652037409593, -0.25959276401017695, -0.22644290433598943, -0.18934157630184492, -0.15635933720211706, -0.13098819127111425, -0.11703468889545775, -0.11610010078089412, -0.12305995818540588, -0.13523997315574104, -0.15124035217991041, -0.16553143255351685, -0.17243158342807094, -0.1689746282882985, -0.15499047333767932, -0.13253135253940218, -0.10386386819932406, -0.07083083271479777, -0.03564210099155827, 0.05820839068418109, 0.11287996530649792, 0.1648577655927122, 0.21057833534146542, 0.23261424641925177, 0.21587297376111256, 0.16507456977946014, 0.0948923457013221, 0.017682482339689637, -0.05813445348717686, -0.12627659430518115, -0.1810676317926517, -0.21798831704481694, -0.23417612162015267, -0.23207849780731807, -0.2167904906118187, -0.19525275101765477, -0.17157937624413216, -0.14167678876815484, -0.1023837535581219, -0.05850989045047352, -0.023130308073780786, -0.007944123203306439, -0.017608643180069307, -0.04782612460302697, -0.09055264144517126, -0.13619294197085038, -0.17414045655052715, -0.19714720424868493, -0.20236192788634338, -0.19154761694012246, -0.16910904137078211, -0.14336905809203013, -0.12107683519033553, -0.10440861530923583, -0.09606779745922125, -0.09556500929838806, -0.09893515137064596, -0.10552528931283105, -0.11484425946775645, -0.12289660476501649, -0.1253882589708264, -0.12005768597667507, -0.1068279491175574, -0.08804848650541325, -0.06684084241805786, -0.044894314019976546, -0.022592966921991524, 0.04092504789760788, 0.08177672993231665, 0.11984704019757565, 0.1521937581125785, 0.17042489700281135, 0.16117396310567897, 0.11978788035000656, 0.054948921419788806, -0.017859307807219886, -0.08427149124584613, -0.13688674083851854, -0.172502636820561, -0.19070723121312624, -0.19324803943009458, -0.18347968375951676, -0.16725436391976556, -0.14914173219489604, -0.13138642520482757, -0.11108619801134878, -0.08524482808025477, -0.05341981745116194, -0.022382471181028134, -0.0023876057789390843, -0.0006791318640572332, -0.015580134760591401, -0.042501317207833685, -0.0750655225371515, -0.10545353796138988, -0.12561777188592765, -0.13341443446446732, -0.13023378322994117, -0.11855527235372157, -0.10378477131619551, -0.09002184434073622, -0.07914372833165592, -0.07217720848156585, -0.06861491563345376, -0.06854172334594405, -0.07292935089197478, -0.07987182009149957, -0.08478369732619169, -0.08439906019498113, -0.07783963524278888, -0.06561754641339691, -0.0501226295147772, -0.03490433702564488, -0.022018084865523497, -0.010871114770803565, 0.023828485810924824, 0.050213405567694096, 0.07475404437924231, 0.09373449842872651, 0.10560612189347214, 0.10267545062603754, 0.07586020775623288, 0.027124930738724205, -0.03064852182545963, -0.08260160221657906, -0.12030580785343209, -0.14204872349500483, -0.1484418668498054, -0.14286057945678246, -0.12988773963317582, -0.11533099482817741, -0.1032090962721869, -0.09307813177750493, -0.08248324278651774, -0.06904429162019328, -0.05098065513438916, -0.02957388066446396, -0.011878620829104224, -0.004259299119607143, -0.007573211284761714, -0.019767122104407096, -0.03832536052500799, -0.05795009518349285, -0.07208916596594415, -0.07921718688219066, -0.080023006843108, -0.07559638981147136, -0.0679679378075872, -0.059771695628415514, -0.05263066262453199, -0.04617516026888773, -0.04099499396992274, -0.03973923534485649, -0.04364514374016919, -0.04967059099157782, -0.05276049066937879, -0.05060810219988146, -0.04420117827058665, -0.03489416367673993, -0.0241069281446535, -0.014388067438330597, -0.007807133532954638, -0.00366395014273333, 0.010524026521625766, 0.023074117435549636, 0.03482741888735773, 0.043365523576692516, 0.0492952002694859, 0.04936157964539077, 0.03668670160170752, 0.010572014585912221, -0.021613391512061406, -0.05061543355815171, -0.07068210775648572, -0.08113946632871226, -0.08252027520603152, -0.07693561528047721, -0.06796921731391478, -0.05928838807421922, -0.053593529554551815, -0.04969373383231921, -0.04592208988885551, -0.04090408770773173, -0.03350167606467012, -0.02309045806683019, -0.013044630318917585, -0.006909541345178872, -0.005973117468003795, -0.009556132096210188, -0.017316676659901165, -0.026395226899456167, -0.03336946216040282, -0.037217427193238166, -0.03833597617031121, -0.03694428850826347, -0.0333589852198614, -0.02934888503293671, -0.025697190663112487, -0.021784780282547617, -0.01839947936576653, -0.017593339765569642, -0.020218835832658526, -0.02407044548838247, -0.025621266447655174, -0.023623201735654287, -0.01957142822059729, -0.01476247148951922, -0.009562283384033888, -0.004981172497829307, -0.0022684512912463377, -0.0010245916721617094, 5.568001497418895, -0.008550693633955336, -0.01657631114988028, -0.022696191391277945, -0.02548634808172982, -0.024758046264675225, -0.02131408336684581, -0.016148169224333837, -0.010744102281530459, -0.005884984731223331, 0.0011831198156515151, 0.014027312503264337, 0.03203724713369691, 0.05211912182205603, 0.07367377760373708, 0.09621454880283346, 0.11522407798527873, 0.12561503989765826, 0.12473507681142931, 0.1130377125162856, 0.09290946775896103, 0.06664213067080987, 0.03441341339998833, -0.003378427598677342, -0.045163544626725026, -0.0887448451010573, -0.13140033077622126, -0.17112449086344617, -0.20771611812001362, -0.23921188029802323, -0.2613148643560218, -0.2739220964382158, -0.28135184095778437, -0.285099352021112, -0.281798162840915, -0.26921750451235127, -0.24857409700139863, -0.21982185804972448, -0.18048585592126654, -0.13081369661212242, -0.07738632574666274, -0.029923405893668525, 0.005268761127894516, 0.027816925812918305, 0.04035178184943164, 0.044894131795133636, 0.0419398708584622, 0.0320978640525614, 0.017262355161718857, -0.018427443287720342, -0.03568619066328946, -0.04972568810156402, -0.057514628962021475, -0.057384384237104714, -0.05057730377395434, -0.03969796861830501, -0.027417670015723677, -0.014523518001325003, 0.0032204060613001354, 0.031035323025199044, 0.06745229558756295, 0.10715314167167482, 0.14857457114174374, 0.18951362523547502, 0.2217382499449443, 0.23689774501125274, 0.23161666189599006, 0.2081589087238865, 0.17198115180550283, 0.1273665324052858, 0.07318265586701181, 0.006542824593309567, -0.07216969216370117, -0.15955731587402308, -0.2488766656667406, -0.3322459495708232, -0.4065084805207693, -0.47015323833746014, -0.5180382617288581, -0.5484730174144434, -0.5657600700180038, -0.571666415631114, -0.5623031198928918, -0.5346367586887806, -0.48969528326645456, -0.4281951699549347, -0.3489395772713302, -0.25419338810766295, -0.15440678684029893, -0.0647952794952474, 0.0033308417621209225, 0.047587196562240267, 0.07207913330186556, 0.08140637063645838, 0.07721545715807425, 0.060176345938323356, 0.032875118739464505, -0.030403964046368876, -0.059291314022477656, -0.0843713620493913, -0.10020834277808571, -0.10222341276094807, -0.09195445213276536, -0.07408075777120011, -0.05195947536354493, -0.026011132276259858, 0.007647554410978299, 0.05328490293150656, 0.1082369123040308, 0.1665717847151644, 0.22559206705727344, 0.2796861709748322, 0.3168928002755305, 0.3271599464543697, 0.309120649294118, 0.26991963818150916, 0.22103175005603484, 0.16982159581013193, 0.11165041601618833, 0.03427513460876773, -0.06877520503853328, -0.19476368468087196, -0.33257707008165444, -0.4655890339299664, -0.5830631739320088, -0.6829548493056249, -0.7618457638532663, -0.8159556990612798, -0.8463013587122378, -0.8537321585090645, -0.835900790558941, -0.7903678852617128, -0.7172900484186598, -0.6195949961137446, -0.5018280006597479, -0.37003403592400685, -0.23442198707700643, -0.11026365661360464, -0.012256555210306951, 0.05337283265000287, 0.09043919522054, 0.10605666555497047, 0.10347926525480085, 0.08284966560088404, 0.04623025435494817, -0.04403587525101972, -0.08687366183540463, -0.12537158334235057, -0.15076234421641108, -0.15527195179882763, -0.14066263597472276, -0.11353667305420406, -0.0778904490787481, -0.03445371069276905, 0.018762414605275043, 0.08333633525710882, 0.1555795099409223, 0.2305243228108093, 0.30463739566689746, 0.36805049841065907, 0.4040608280688506, 0.4005411137119863, 0.3592096538264049, 0.29491187281782366, 0.23056404667406563, 0.18069442826717128, 0.13647620620819284, 0.07111909170450319, -0.0355398334329543, -0.18492357760538528, -0.36302021744399154, -0.5453322198206112, -0.7108893776114624, -0.8524952128647414, -0.9677162756407252, -1.0517159988552227, -1.1014116298128986, -1.1148497818908185, -1.0903720073421916, -1.0275696028163162, -0.9273620240465069, -0.7957314374680692, -0.6443749487225237, -0.4839001133259761, -0.32220835376667434, -0.17137968148182187, -0.047388100646746006, 0.03984626927662452, 0.09196344068181017, 0.11670405110736444, 0.1188245355364047, 0.09829568512739882, 0.05612477767629532, -0.05824868799844914, -0.11546654788685098, -0.16660782430474042, -0.19967889235299843, -0.20474377926132376, -0.18385264541520646, -0.1451170782869293, -0.09350830098738182, -0.03130383647956818, 0.040824855235091446, 0.1222419885486233, 0.20956026030010624, 0.29962189154648694, 0.3883968029458324, 0.4618143617110849, 0.49696549365201936, 0.4770261779350252, 0.403833300156743, 0.3005643685863784, 0.2074583984690922, 0.15359283132802662, 0.12973136164286073, 0.09422583637408466, 0.009225466684026599, -0.1371080934131536, -0.3328933499354012, -0.5501464218097756, -0.7591932980730142, -0.9443722510737431, -1.101341540643582, -1.2245139190139995, -1.3056666796635172, -1.3370303252672897, -1.3147131786166943, -1.241020961221207, -1.1206680010417995, -0.9629526914540764, -0.7846302689799285, -0.601088280067467, -0.42000794667388114, -0.2500666210364678, -0.10554877086844391, 0.002819174107964653, 0.07357530258878008, 0.11133433820070905, 0.12094664602229123, 0.10370556885076737, 0.06054028537871604, -0.07247876847951172, -0.14174501147282928, -0.20046803601209642, -0.23538993786409065, -0.23666010906659582, -0.2072881953681611, -0.15625439766590693, -0.08965562439548101, -0.01216776464467406, 0.07384515812961907, 0.16822594870137692, 0.26946663574344326, 0.37614381282561793, 0.4839437664346685, 0.5745084586560315, 0.6172454045473403, 0.586326446227298, 0.4775938110335341, 0.32168303423935407, 0.17878319437017184, 0.09941777266749822, 0.08322566283154077, 0.08145145557606549, 0.03952313061485927, -0.0716771539768484, -0.2517142879640717, -0.4774096579426828, -0.7155304533326196, -0.9416639497424034, -1.1455666696963203, -1.3183226439601747, -1.4444689298215867, -1.5084705545350925, -1.5023770583329532, -1.4297547154919312, -1.300120042408282, -1.1262976632027308, -0.9275097414360638, -0.7235095030790087, -0.5260819003846255, -0.34276089044347496, -0.1834795362973982, -0.05633263356030447, 0.035248383202960594, 0.09021047515112439, 0.11033086551927411, 0.09874917379950518, 0.05877070723272341, -0.08548125342424949, -0.16167300220460237, -0.2196135933165868, -0.24826696681012106, -0.2407497931220116, -0.20173132565740734, -0.14039995037082234, -0.06414958794250165, 0.02115784157339477, 0.11465882869669423, 0.2185259111185694, 0.33306860497738233, 0.45836492995293265, 0.5897741820371274, 0.7051783974322096, 0.7668155793963373, 0.7359092502100929, 0.5974283252821376, 0.3861441685023998, 0.17849970055691056, 0.04804007877430283, 0.014007530351396598, 0.034053853899901995, 0.04264348642269747, -0.009204749199093087, -0.1416348072580119, -0.34698158932730777, -0.5962518061315382, -0.8578065030320126, -1.1112077583640945, -1.339419820322623, -1.5181898449525844, -1.6241397570770237, -1.6463235621164556, -1.5879377994600827, -1.461272920102921, -1.2825258870485101, -1.0720186561021998, -0.8515816584027618, -0.6388964857825018, -0.4442979344453125, -0.2739804870153955, -0.13232269582652753, -0.022309134780622786, 0.05156204487354362, 0.08601966512025039, 0.08350953597607076, 0.05087444715873544, -0.0932709601700671, -0.16881966119470088, -0.21745569581150073, -0.23341758359027093, -0.21438051009992887, -0.16674029147667677, -0.10053844052499387, -0.02357761072383095, 0.061569562042559534, 0.1578159691735421, 0.2681936040241616, 0.39310783804195454, 0.5329606943465791, 0.6827106929886071, 0.8205209325484143, 0.9055408006766823, 0.8867778860939949, 0.7360714143282427, 0.4834645239181242, 0.21351994346978756, 0.018806796289807963, -0.05649910085458943, -0.035661931678126015, 0.014959607967323827, 0.029861506994370447, -0.03535666233920693, -0.1975894316466977, -0.44083466392481807, -0.7288503956989114, -1.0282290562328182, -1.3096309355576181, -1.5398375493757566, -1.6886538471540216, -1.743230751306497, -1.7067078000751477, -1.5923463485973315, -1.4194660682386737, -1.2097720584059162, -0.9835510344919897, -0.760047557669054, -0.5545607917808634, -0.3740627590318417, -0.22153815090855616, -0.09886016117260761, -0.009000746780621021, 0.04277871531753082, 0.055355592108074704, 0.036369508319271666, -0.09065016430373231, -0.15655940601996846, -0.18975414255657638, -0.19040771444399693, -0.16060833819265402, -0.10938734610200627, -0.04820479113145155, 0.01935070894298958, 0.09865440908387428, 0.19561433760196575, 0.31101374404813065, 0.44113698615097274, 0.5831746945958501, 0.733268711913509, 0.8767409894474512, 0.9767546243797585, 0.9778455290215263, 0.838220075707825, 0.5723473813466967, 0.26141264887731647, 0.00895125110994108, -0.11729306772012241, -0.11600874165337952, -0.044159455116573966, 0.024094597077347745, 0.025116641806792395, -0.0836262875177493, -0.3056840569462396, -0.6055671501399587, -0.9376189156338246, -1.2595654449205025, -1.530038432230222, -1.7141981837002909, -1.7974106681938566, -1.7834545775834603, -1.6856140717787704, -1.525133893516338, -1.3268689652505166, -1.109351064502025, -0.8864368215778469, -0.674175169639443, -0.48415642625755906, -0.32200479476501276, -0.19039467147097056, -0.08911369884799916, -0.020138470114086832, 0.013108178269937295, 0.015167278364857912, -0.07500913939390569, -0.12235362391763105, -0.13612194044109785, -0.12135629694618913, -0.08508029638166813, -0.04029958823993126, 0.00352496300746083, 0.053506887606530454, 0.12513753335683062, 0.22583680505207934, 0.34896957615962765, 0.47965006568777, 0.6090866396652576, 0.7363733894614511, 0.8581363018630259, 0.9517395789613764, 0.9698690215785092, 0.8608733100871192, 0.6177854779065305, 0.3032994446275031, 0.01844354640997839, -0.15326843627791864, -0.18707285387461145, -0.12241901744380176, -0.03188662536693633, 0.011404369100714113, -0.052892645571917626, -0.24763908049711977, -0.5439572960002773, -0.8874148369126728, -1.2260107124346231, -1.5130407862899455, -1.7130339934412913, -1.8127810436592813, -1.8179524441876829, -1.7402237756314907, -1.5973943148092482, -1.4153922548819697, -1.2155105489311966, -1.0062904889740574, -0.7973619188434465, -0.6024211823387227, -0.4315943624310473, -0.2908622984736167, -0.17981034841095908, -0.0956723411090536, -0.03996607721382118, -0.011653622904380613, -0.047211665346719806, -0.06882936390160188, -0.06107276657489179, -0.032825105372575464, 0.0024669019313459726, 0.02892999829780274, 0.0455522939435839, 0.07513846161082373, 0.1441731151720033, 0.25822171664423366, 0.3959451667101256, 0.5272246495179465, 0.6358339861487672, 0.7199107176532344, 0.787980565779812, 0.8451674385604568, 0.8662670967136139, 0.798172178931662, 0.6111238949641494, 0.3368365184859819, 0.058138668959675205, -0.14125711978389915, -0.21941243089560916, -0.19168710531130437, -0.11730033757443209, -0.0694581974768172, -0.11585600142411848, -0.29178953172585786, -0.5774566445739695, -0.9141837743557364, -1.243528714016112, -1.5176303900562131, -1.704500567795189, -1.7984093524908729, -1.8119561211289046, -1.755708858569179, -1.6380574295985944, -1.4774401301815046, -1.2976960222798977, -1.1089995415905411, -0.9139855866637288, -0.7225311933299524, -0.5465478638150127, -0.39575251680726387, -0.2736165387911234, -0.17562453780684326, -0.09858529849214619, -0.042175653030629125, -0.010378753631655791, -0.002308160531197377, 0.026122452717293826, 0.0631989236960799, 0.08888459767281208, 0.08789774202884962, 0.07395407751784112, 0.08891692690463565, 0.16796234735937066, 0.308598004323181, 0.47173689367185967, 0.6109552775324496, 0.6980032909963033, 0.726223348130044, 0.7171767727003817, 0.7110157113984308, 0.7136244095117722, 0.6797903748281878, 0.5602033787669778, 0.3547306395229837, 0.11730952646691303, -0.08609577485044208, -0.20677342750508085, -0.2351478239854198, -0.20869273493066953, -0.19159421232704676, -0.25000874253891814, -0.4229860839611146, -0.6980457292470691, -1.0186289359646323, -1.3235407733674003, -1.5661019226081634, -1.7187111013849454, -1.7834672693999836, -1.7848236979303214, -1.7390342466382585, -1.6465392060124016, -1.5124102354092228, -1.3555099125558898, -1.1891449396200995, -1.0134849763964247, -0.8330575247481707, -0.6578918865262786, -0.49869044821438796, -0.36411514358671554, -0.2524144519543314, -0.15633627935168606, -0.07323181714758252, 0.030102851922307255, 0.06810727639067146, 0.11384118959508739, 0.15342999684224004, 0.16190231062528324, 0.1297339892494426, 0.09082155604177151, 0.10526156445094918, 0.20975340138332096, 0.39019307111667373, 0.5913875756746757, 0.7478109300421112, 0.8162573652324174, 0.7882405890860572, 0.6988082481078385, 0.6158381548791345, 0.5745008607112133, 0.5451922521409757, 0.4702263544455214, 0.32762459841690056, 0.1414210951889232, -0.0478616115789334, -0.19482569366894417, -0.2737065331087137, -0.3025633332215206, -0.33168750063053676, -0.41802847243453556, -0.5985035220713405, -0.8640158111059507, -1.165046471349473, -1.4427600721875546, -1.6521426896648443, -1.7693108053902864, -1.7985394319972743, -1.7705484197989778, -1.7140570490466651, -1.6323075139376453, -1.5203823824262588, -1.386944992027, -1.2434383796055095, -1.0886698269484754, -0.9232911633797415, -0.754977763823514, -0.592090516222511, -0.44558466808724123, -0.31962060524691527, -0.20679426243712573, -0.10094671860529847, 0.06754358311490401, 0.13221757506495463, 0.19058058026664898, 0.22602132257089425, 0.21244138416408861, 0.15297597542293512, 0.10335165755036531, 0.13446386476392141, 0.27699769718540035, 0.5053833840888993, 0.7506512905340946, 0.929819054659247, 0.9866710169561288, 0.9132467998561096, 0.7558821538482771, 0.5964814106514659, 0.4903977784113356, 0.4271375650748225, 0.3544606409356526, 0.24114978561638675, 0.08930833165760046, -0.08097876040905007, -0.23218099299224457, -0.33563831072386957, -0.39929348713193735, -0.4628314706001619, -0.5702140910104911, -0.7558734739311296, -1.01293584407606, -1.2976025878543151, -1.5559926963624877, -1.7432240971804196, -1.8376118004135895, -1.8440959412343345, -1.7890901620779984, -1.7086822153415144, -1.61933975714207, -1.5162503103820495, -1.399335212874086, -1.2753656949512548, -1.1405976541825829, -0.9916192765153332, -0.8340542356257848, -0.6726227472480089, -0.516461904084524, -0.3756975288088562, -0.2474157118233349, -0.12323247018191466, 0.09702065138008377, 0.18256361664347345, 0.2478069564095273, 0.2730656320999658, 0.23760729246679194, 0.16238286964386517, 0.11953704780965063, 0.18040998654604568, 0.3653296268701237, 0.6388827293182061, 0.9241546215030731, 1.1276972793518312, 1.1814448179471095, 1.0796572528725772, 0.8760822510664525, 0.6529083678764293, 0.47588202505124577, 0.35300240974235847, 0.24795759456765015, 0.129550937703356, -0.012955544114864648, -0.16998533101770516, -0.3114136528020901, -0.41494142517225174, -0.4869294963980234, -0.559979627680771, -0.6679627684767947, -0.8454606201092928, -1.0927224984879298, -1.3673039077781899, -1.6198204342609468, -1.8054251011529696, -1.8980802343288556, -1.9020421770878546, -1.837322388696021, -1.7368059357305776, -1.6296291060528123, -1.5210102205943543, -1.4084341432157155, -1.2954498690040854, -1.176278823285535, -1.0423524316919217, -0.8963258909306004, -0.7395729772003284, -0.5767501969579565, -0.4219032147021958, -0.2792542020597825, -0.14036433123153355, 0.11708716195453044, 0.21637234124626037, 0.2823672868879254, 0.2941913757000105, 0.24267128898365217, 0.16602961357751136, 0.1434599939083865, 0.23898679003147408, 0.46111084536490043, 0.7681353659258445, 1.082002294753238, 1.3040947141055486, 1.3599515727444333, 1.248610069859226, 1.0234324269102046, 0.7568045865348131, 0.5164976354049455, 0.32815288114766183, 0.17650096555956038, 0.033636727181501375, -0.11727124219304774, -0.2678364561800298, -0.39573607891157647, -0.486324566600526, -0.5495812475465051, -0.611630072474087, -0.702354050771647, -0.8563728230029545, -1.085764591018419, -1.3519908748543397, -1.609151060041222, -1.8161269453634847, -1.9359935312458911, -1.9620963376555143, -1.9074442570555479, -1.7984498268483116, -1.671940201737811, -1.5472924302784932, -1.4263857465233485, -1.313228091254224, -1.2023355348858378, -1.0794396274968028, -0.9427403339699806, -0.7918058247398534, -0.6260748733004612, -0.45973539662209206, -0.30407095895643366, -0.15316677838505355, 0.12749925027543235, 0.2330469285717392, 0.29521034613812897, 0.2947084727817422, 0.23633543434825774, 0.1711121434528837, 0.17667121207578027, 0.3045032065360822, 0.5526604334801003, 0.8781139783941767, 1.2031896113529499, 1.4283383199154795, 1.4837604908313735, 1.3733230610352252, 1.1447087062593033, 0.8585180936048672, 0.5784454004629155, 0.3424493289968388, 0.15130213784353796, -0.020057335746055418, -0.18622338042039077, -0.3375461371880098, -0.4595457968779009, -0.5390956122607382, -0.5852727305633919, -0.6204025936706006, -0.6760851113935752, -0.7904387783760973, -0.986182650805011, -1.239424966616259, -1.5100076425430289, -1.7590971615469773, -1.935833775154145, -2.01233005982091, -1.9896340239674344, -1.8861064733034174, -1.7437324166304835, -1.597934741073934, -1.4591575177649176, -1.3346458826842076, -1.2228109907860698, -1.1056349954916376, -0.9753254684641908, -0.8304470513320822, -0.6660527909293802, -0.4922426672703028, -0.3248548580530691, -0.16310320970449307, 0.12820103211752829, 0.23303498883630308, 0.28924689801012926, 0.2812101540742483, 0.2266137853313513, 0.18259992505363729, 0.21809690942928245, 0.3716806980879808, 0.6345117927549903, 0.9620906198127247, 1.276820592844262, 1.4846536198223323, 1.5280796591896384, 1.4163069025052357, 1.193972841978908, 0.9162235218160362, 0.6377151621185063, 0.3920175939229849, 0.18251920685792156, -0.011806204090630467, -0.19732170801783142, -0.36583034910145584, -0.5080641651415231, -0.5988273209126569, -0.6311996768230386, -0.6245110833759624, -0.6179097856009509, -0.6657637068886473, -0.8024645198629639, -1.0255006180324038, -1.3114457067125984, -1.61927292849726, -1.8773489796808223, -2.028967405968055, -2.06024801482678, -1.980644584668366, -1.832639986962998, -1.6669136561008044, -1.5055797687458683, -1.3606850490927391, -1.2380426599879102, -1.1208358189005139, -0.9952290127243104, -0.8576155510949734, -0.6990993533047692, -0.5226865637179986, -0.3452618276254781, -0.17254140237967516, 0.12069677132001022, 0.21931710989716008, 0.2696199946438411, 0.26069532854658556, 0.2188432351191099, 0.19958998108681444, 0.260633502206129, 0.43171690195327056, 0.6980829424713294, 1.0107828638347076, 1.295633621000552, 1.4704054434207616, 1.4900333221276167, 1.368535135739921, 1.156438309256671, 0.913360542337921, 0.6801968873861886, 0.46965861366784883, 0.27328805616978213, 0.07235388145400466, -0.13513905714272034, -0.3454225582247941, -0.5425158636944061, -0.6767695169027577, -0.7160657229927228, -0.6688688633473228, -0.5804983025603413, -0.5315982222876661, -0.5816496352073747, -0.748663371651217, -1.0321354446360593, -1.3959931226586277, -1.7468675152413733, -1.9913403528716958, -2.09399221921868, -2.056156429930622, -1.9175875240151583, -1.739752743629917, -1.5571394760944892, -1.3876498287142205, -1.2465627332017135, -1.1239097961969648, -1.002125961929681, -0.8736773333913567, -0.7253567376543716, -0.5516671692003129, -0.367108682812653, -0.18327567354865454, 0.1079304653213965, 0.19720564698462292, 0.2428979070927709, 0.23791875488519304, 0.2123556876660173, 0.21621040575719283, 0.29569403651754245, 0.47237581040588317, 0.7268716306769739, 1.0093015982869884, 1.2529291548013106, 1.3889770427083976, 1.3812660566975015, 1.249438324352161, 1.056370500632173, 0.8681049745805235, 0.71172401819489, 0.5734982591741504, 0.4242212485722997, 0.240092889086315, 0.011571744390493527, -0.2575844904542562, -0.5273505780851446, -0.7273667800619362, -0.7972579725813866, -0.7313792876519668, -0.5760858208865863, -0.4266348907761619, -0.3764208487222501, -0.4726442141141544, -0.7329048366166785, -1.1295769937781095, -1.558319872820933, -1.8951743428437866, -2.077331087972083, -2.094321987074671, -1.9802044513416401, -1.8019811066291325, -1.6052387126475627, -1.4136909251407632, -1.2516503376405868, -1.1195461528320334, -1.0000288681217917, -0.881265625252169, -0.745251926291251, -0.5781046233184879, -0.38969202146221854, -0.195378154261045, 0.09293569612674475, 0.1716394350682112, 0.21347219586130162, 0.21377266871413278, 0.2032168582157665, 0.224526009448312, 0.3123120251287191, 0.48071217149495865, 0.7081752293775422, 0.9485764474440898, 1.1469346697229115, 1.2474804996297673, 1.221691928451275, 1.096515942060931, 0.942640541426729, 0.8248361001751067, 0.7571859890498367, 0.7075777286321011, 0.6296993894120082, 0.4842703180091718, 0.24712409473279193, -0.07517249551447099, -0.4250822634412461, -0.7057724029571318, -0.8210590624087445, -0.7519167926808925, -0.565374515270359, -0.35673145524104144, -0.22854880341644285, -0.2574471301421206, -0.48203592158241937, -0.8847929894056432, -1.3577108429701115, -1.762103485843811, -2.014430314882374, -2.0900673294983525, -2.012753113904946, -1.8471717585484937, -1.6465251859954788, -1.4402973228112226, -1.2601122073201207, -1.1172882848643455, -0.9978207163723293, -0.8868280025652675, -0.7619077853126496, -0.6018796701904545, -0.41132957931775127, -0.20757129749938963, 0.07779447142464259, 0.14575326167780434, 0.18371594674168656, 0.1875221838519109, 0.18562065659710578, 0.21393495104414842, 0.2984168991703433, 0.44729470343267574, 0.6375939884998857, 0.8307850860269227, 0.9871842208199194, 1.0629125198825307, 1.0378854285779193, 0.9459206930760623, 0.8545432531049364, 0.8157933256237014, 0.8332816391183199, 0.8668872245327762, 0.8631518250482197, 0.7712405249388926, 0.5465350547479833, 0.18922915288933273, -0.22535019756428107, -0.5683988613552583, -0.7302848246964244, -0.6827811469316701, -0.5026549320214456, -0.2919346439810908, -0.14339168010555067, -0.13819002441744224, -0.32511842894418846, -0.7062285086018101, -1.1853052444211853, -1.6218074275048142, -1.9233650279829015, -2.052169931052469, -2.0175589905883338, -1.8745162843787213, -1.6789370755138802, -1.4665440394207534, -1.274724469625786, -1.1233517040662562, -1.0026687073682166, -0.8963378824147505, -0.7789241105050326, -0.6238272629022907, -0.43104435858803397, -0.2187597785636212, 0.06356102356027035, 0.12080841642762206, 0.15363564270460572, 0.15673120816848532, 0.1548810432599032, 0.17883637291198806, 0.24836342137457404, 0.3682550470461538, 0.5180190060143132, 0.6680592696802162, 0.7921163821775111, 0.8573551315481226, 0.8523742801853577, 0.8153052772063427, 0.7990897359810596, 0.8344203917250065, 0.915940925766748, 1.0028327977342404, 1.0521380068935382, 1.0097035594978159, 0.8134146351263978, 0.4653614106923835, 0.054622708661457416, -0.2872109456433431, -0.46339945495086915, -0.4619883769641651, -0.34382736623350396, -0.1888552178771777, -0.07683167812382756, -0.08060838046815914, -0.24782060509220963, -0.594290651696095, -1.0520479833897227, -1.491168190570137, -1.8195788710609757, -1.9901255554618644, -1.9967703066205882, -1.8811323824962587, -1.697556849523135, -1.4873839824631638, -1.2925762814905708, -1.1380006126009425, -1.0167940718977426, -0.9123649148752151, -0.7983265360214382, -0.645020100229572, -0.44905743050649594, -0.22883478410142702, 0.04929134328193271, 0.0944079578945803, 0.11950794628357767, 0.11782224704947353, 0.1094631303580129, 0.12031989880914676, 0.16608041847290786, 0.25140140968466695, 0.36126898406775587, 0.4751302703399263, 0.5781210248867551, 0.6471249088807481, 0.6758453074480252, 0.6998255485124524, 0.7513697820078156, 0.8368374278845858, 0.9470110455896472, 1.052783998618044, 1.1211607599360363, 1.0993589643313366, 0.9314147035254984, 0.629649522781259, 0.2935935191038431, 0.023917445467426808, -0.12877353318527865, -0.1627899552543877, -0.11171747206000619, -0.031082864190727037, 0.01679739013032318, -0.02145859746870406, -0.1910499814468077, -0.5080731707712729, -0.93772981248208, -1.3679893750287815, -1.7077263478134674, -1.9059392650762448, -1.9465958276312652, -1.8592404172313861, -1.6938350357229115, -1.494927861956516, -1.3070169010477, -1.1565903413800733, -1.0377483781665782, -0.9339853733141649, -0.8198771399644967, -0.6654528601971637, -0.46544354878174293, -0.23792563716530069, 0.03213061759033511, 0.06131915131478178, 0.07487020339429587, 0.06529488931357967, 0.047811545118216704, 0.04336593282066078, 0.06341097653319573, 0.11257482160053266, 0.18352125579784706, 0.26655861651157314, 0.35626550753991126, 0.43718838206087224, 0.504139234398254, 0.5822154935272383, 0.6813419749630633, 0.786747272871221, 0.8932945127852433, 0.9882668936812784, 1.0379304880933256, 1.0055241463130387, 0.8662145832251817, 0.6280534874903136, 0.3896550020434692, 0.22295337184155084, 0.13412980895470555, 0.10990483038578616, 0.1286769813769802, 0.15693039238124104, 0.1558479163843099, 0.08789882844894381, -0.09918545990686016, -0.4077956749870811, -0.8192996974136995, -1.241843102201753, -1.584509140099262, -1.7970312958215673, -1.8624949576139649, -1.8024443006637565, -1.6601362103414403, -1.480345674643825, -1.308506585438684, -1.1702285556929881, -1.0583309436492907, -0.9559931734117988, -0.8399495803132221, -0.682454695838294, -0.4783393109497952, -0.24505367297865113, 0.00872927743207696, 0.015766385504798183, 0.013323087982029816, -0.005577076002880108, -0.031198749231872634, -0.04804666159154808, -0.04921201351248878, -0.030878354183112723, 0.0053348118012320825, 0.05921337317261196, 0.135571879421287, 0.22634097656058388, 0.32559486517311814, 0.4442635825592008, 0.5690223813935184, 0.6719108981537688, 0.7538574807596037, 0.8028554043231778, 0.7857677598614179, 0.7167155172230897, 0.6134940762344325, 0.46310981145516217, 0.33482150067228394, 0.27768583650191186, 0.2748166564407746, 0.29636570055964473, 0.3231767438140777, 0.33905519739072176, 0.324347637550602, 0.24800891227284505, 0.043726257711461484, -0.278598003176551, -0.6892254369283951, -1.1081381708507334, -1.4478979926709195, -1.6639703716321637, -1.7455917754838424, -1.7100623352877071, -1.5933006083429537, -1.4381990390374235, -1.289381053106752, -1.1696552711025954, -1.069013974965704, -0.9697647978291702, -0.8514337770316304, -0.6906312924284808, -0.4840203662373184, -0.24823411205155668, -0.022531935501674066, -0.04466888958025447, -0.06747445995332983, -0.09599085467071936, -0.12667888364081292, -0.15004063865550257, -0.16316750807193553, -0.164588738669978, -0.15456764824951533, -0.12817797578394685, -0.07147712712859187, 0.016065519622104858, 0.12932743076893427, 0.26863976011877766, 0.40293609757580945, 0.49058380184167705, 0.5304056923815241, 0.5133528156634816, 0.4212915244447912, 0.3113195306660658, 0.2295135852942136, 0.16037934680495597, 0.13724058664694486, 0.18945622986974112, 0.28350815223733467, 0.36923153689027743, 0.4279563386150484, 0.4644605444079615, 0.4671488558969476, 0.4061100958978206, 0.1977183675777175, -0.1427512234347841, -0.5581198430640947, -0.9692441775904709, -1.2980279713702545, -1.5096410330914138, -1.6004999498523953, -1.5854598442689463, -1.4944726276537654, -1.3675386525932345, -1.2461634045982852, -1.148598088315663, -1.061510010564026, -0.9667331239375156, -0.8473018560828602, -0.6852739435927767, -0.47973447701157346, -0.24616964413512496, -0.05980652800823544, -0.116312477915788, -0.16274426887648027, -0.2008413321411153, -0.23286205176004354, -0.2557078705557128, -0.270755698530371, -0.27948291537149067, -0.28373836524010143, -0.2800701030668541, -0.24942831732398554, -0.18191648515694725, -0.07993985695904138, 0.05378390479452199, 0.18105507886189767, 0.25025848089070957, 0.25840561495642483, 0.19943653271945178, 0.05825392137275614, -0.08617078562812144, -0.16269867756246756, -0.18488880075089092, -0.13505175307279138, 0.0010366648891969735, 0.17955486624128716, 0.33106052346735415, 0.43382854557439016, 0.5075510021031646, 0.5440950831148933, 0.5082899812819069, 0.3092617156980683, -0.03348867197005856, -0.4407009712786485, -0.8301910359365101, -1.1380639364967637, -1.3391556545259222, -1.433042706548638, -1.4327359240939435, -1.365235408878664, -1.2676411466353261, -1.175858077093667, -1.1020029061980585, -1.029826545814602, -0.9416999616869155, -0.8244924536469188, -0.6654508264494787, -0.46564480838960887, -0.23913616335374543, -0.09783271493799639, -0.18945210935662354, -0.26068893164889134, -0.3087291231343534, -0.33996939856186187, -0.35700702086375674, -0.36504879901576637, -0.36980007297344625, -0.3764672062373124, -0.38669353717858684, -0.38326213303719875, -0.3484612520090899, -0.27877920454539884, -0.17433684775163052, -0.06867308565040782, -0.018580658810486494, -0.03322382342841796, -0.10659483055151825, -0.25382578294619546, -0.41703776678924687, -0.502482653860265, -0.5065130417863681, -0.4126727927411973, -0.2188045254865672, 0.018995682145852896, 0.22371957855048302, 0.3726856061027058, 0.4850900665775249, 0.554860723672407, 0.5369967725765105, 0.35398629152547684, 0.032096439992613336, -0.3424462457972376, -0.6938052102932906, -0.9727570563625926, -1.15822240176583, -1.2482055921828095, -1.255145289858316, -1.2066240847407668, -1.1369243663326691, -1.0747485346128458, -1.0256139949711094, -0.970896762287039, -0.893684123959543, -0.7839435485119143, -0.6330072383817564, -0.44338066422446964, -0.2280042470368561, -0.13121530619312755, -0.2534058095445775, -0.3475914292434757, -0.40635057241804556, -0.4370059347254492, -0.4460544229297716, -0.4419920130792529, -0.43442533697863206, -0.43212168979085314, -0.44367310494699286, -0.4605387659131315, -0.4633357710609119, -0.4396725565310267, -0.3791071604320146, -0.3024642437938146, -0.2690442676590296, -0.3046464829945958, -0.39486426387467316, -0.5349775018733516, -0.692357310614588, -0.7845036210135943, -0.7776935795463034, -0.6575641717304562, -0.42976312437608305, -0.15819776350298717, 0.08465975110623405, 0.2748729792038553, 0.4200706991798075, 0.5107052975678394, 0.5014390954479508, 0.34229645579807283, 0.0636561914029001, -0.25815252798657357, -0.5608817762434849, -0.804573749848276, -0.9679782628861076, -1.046682088916821, -1.0544325380463173, -1.020664031962382, -0.9763971728437434, -0.9429716086107793, -0.919652339406254, -0.8857218074006962, -0.8245463151259979, -0.727792467568365, -0.5898208769600469, -0.4144394171897582, -0.21363568892080742, -0.1570188907746798, -0.3017836000271594, -0.4143155758037706, -0.48410264418921467, -0.5160735195986778, -0.5177309436270714, -0.49968796241819324, -0.47508677169334984, -0.45584407725381076, -0.455816579746151, -0.47771285885982434, -0.5085696206773714, -0.5315765924295476, -0.5228473456077982, -0.4820609528661868, -0.46328858390442934, -0.5116406361095945, -0.6227389648472887, -0.7700158513440233, -0.9178492132593767, -1.003195918179283, -0.9821651204336396, -0.8456439292771938, -0.602731166440638, -0.31468887649108296, -0.044251498663130384, 0.18096562459525836, 0.35087572696389446, 0.4496752809791091, 0.4433912018332701, 0.3115160477247676, 0.0847907161763524, -0.1786033963114531, -0.4281364865195551, -0.630524933103579, -0.7657002017075955, -0.8284065089291909, -0.8342586415500343, -0.813357378961328, -0.7924340102577897, -0.78609127949347, -0.788430064406665, -0.7772441240368595, -0.7359243254335264, -0.6567959461626769, -0.5363688734469403, -0.3794046571573794, -0.19659853892934026, -0.1753940296986536, -0.33454258519154934, -0.45950252671856584, -0.539085916027718, -0.5737399736514872, -0.5692805042705046, -0.5374832903265895, -0.4943057923481468, -0.45392855579110764, -0.43324855300797144, -0.4438734941030344, -0.4821545443675549, -0.534531190737079, -0.5724904512062388, -0.5761281990363397, -0.5820633652373363, -0.6402360794487428, -0.761444676496841, -0.9188344115733599, -1.0660499424426313, -1.146524485811099, -1.1182675292676687, -0.9755633471932538, -0.7306261207224943, -0.43198935508194414, -0.13373363805666985, 0.12300322773437063, 0.3094826317711672, 0.40801393684558906, 0.40331668520912106, 0.2986327919696271, 0.1195945565344733, -0.09006194101929081, -0.2887758606586972, -0.44976100269103864, -0.5548547814538279, -0.6007636917598731, -0.6050619644530252, -0.595788988287479, -0.5950426544166542, -0.6124289938080022, -0.6379176315460153, -0.6487292520873448, -0.6288606840535326, -0.5706825955762342, -0.4719404780893172, -0.3376697639274105, -0.1766225066402925, -0.18753475865982155, -0.3551736182544797, -0.4878077014415517, -0.5743328412633727, -0.6101724069604072, -0.5988880769707392, -0.5529347156710355, -0.490819342527678, -0.4286644638361255, -0.3830707736787194, -0.3703194338214461, -0.3957606995327958, -0.45368638877448264, -0.5221667644658718, -0.5713911811117452, -0.6142519799321148, -0.6923641035201085, -0.8216916625552253, -0.9843140795792323, -1.1354946157465047, -1.2211824673914888, -1.1994835967684594, -1.0623094614263642, -0.8211072124387323, -0.5117895818145756, -0.1880882836133082, 0.09375767102285718, 0.29253416593357695, 0.39374461143752404, 0.3974916394605653, 0.3186601198474939, 0.17863005173155924, 0.012943739667945937, -0.1436614798714194, -0.26732038435160055, -0.34407590094624646, -0.3755777024543414, -0.37968193127064387, -0.3806230803775884, -0.3967112082171783, -0.4334095096970562, -0.4773853487970316, -0.5070239491570699, -0.5079166518457237, -0.4720380378642862, -0.3974447374118206, -0.28888576858690007, -0.15299818628372658, -0.19310319992968383, -0.3651179358903908, -0.5023355327132814, -0.5926609029904624, -0.626435906479561, -0.6050615100682397, -0.5426304092980605, -0.46025070196724127, -0.37649968966474373, -0.3070095947543642, -0.2675228423628091, -0.2686205119988593, -0.3129556318491094, -0.39117980855428325, -0.4754824349985941, -0.5552877931108349, -0.6572671412418819, -0.7984177759813335, -0.9660550774255785, -1.122042425113484, -1.2172648482152806, -1.210082723176582, -1.0862160362487683, -0.853944862706362, -0.5433497734041799, -0.21061319613917193, 0.08257306835741508, 0.29158861468176484, 0.4010693918504309, 0.4183871969275456, 0.3630495626969473, 0.2553997838697836, 0.12589023112397438, 0.005675811807009066, -0.08465831954403066, -0.1381474212093088, -0.16055420024263783, -0.1678743444823234, -0.17973270461634608, -0.2107736262243248, -0.26266320142830996, -0.3200663159687985, -0.3641026280973481, -0.38274581979713607, -0.3679605094612207, -0.3176869531494309, -0.23569268456115253, -0.12667841676050628, -0.19160662209165882, -0.36333131682659503, -0.500898484546959, -0.5906851642131474, -0.6198356159500952, -0.5869291259007974, -0.5062538677374295, -0.40205731630250324, -0.29671472642274965, -0.20542359660984055, -0.14154057237621664, -0.11696392146199114, -0.1389286216561243, -0.20817696458346927, -0.30794541926383784, -0.4136592917563148, -0.5308158504897207, -0.6756391448529002, -0.8411356064629925, -0.9965658508700679, -1.098838789601923, -1.1087177964894186, -1.0066575471805495, -0.7970512099476005, -0.5078587465173519, -0.19230323549941006, 0.09245022699554134, 0.30263900780648234, 0.4208107436232507, 0.4555583462666019, 0.42402853894216364, 0.34625197811535674, 0.250457543125735, 0.1635807531731641, 0.09915642731112823, 0.05887435828474486, 0.037275454771505165, 0.021889833774275197, -0.0030117593014295095, -0.04854813909750574, -0.11250560095922105, -0.1787918967275132, -0.23209932689660853, -0.2635983105733586, -0.2667515580542076, -0.23935317362196806, -0.1829968217242212, -0.10030268347874532, -0.18489455423216067, -0.3505018430396639, -0.48122834497664846, -0.5635835485694655, -0.584959587745486, -0.5416268137610957, -0.44521901684005916, -0.3204869732176126, -0.19493167175138032, -0.08560716182576056, -0.0014020720336009435, 0.047477975282237066, 0.05083452583782341, 0.0027754930953239197, -0.09130976453384397, -0.2066969058596417, -0.32836876749260974, -0.463812761957156, -0.6124909121308412, -0.7540093888059141, -0.8549439958438266, -0.8804446825054948, -0.8096111271823287, -0.6411458052632187, -0.3983781270991431, -0.1246534424939407, 0.13186372815139746, 0.3321504547123986, 0.4586542389198448, 0.5127211858259141, 0.5053720962583004, 0.4564992204248801, 0.3915772812346548, 0.32938211945789625, 0.2772033373017258, 0.23844361693459346, 0.2107398990035724, 0.18294323751431907, 0.14192335466931796, 0.0814980490098526, 0.008227988339530423, -0.06257583063895937, -0.11968794454879046, -0.1581930917206971, -0.17485617454850733, -0.1675211494572739, -0.13451491223996598, -0.07596858751392885, -0.174238326495042, -0.3279572249133986, -0.44423785832169366, -0.5112912937873155, -0.5202968615140554, -0.46751430561359164, -0.36031556069532056, -0.2199081008608503, -0.07642329931559347, 0.04764418907339828, 0.14531448071838735, 0.2129204521172434, 0.24107102063315675, 0.22009030682219652, 0.14755127847365712, 0.03991343589788462, -0.07759067236427164, -0.19806181149991647, -0.32173807189467135, -0.43821800085476986, -0.5266120488334464, -0.5599360752770353, -0.5191057809590215, -0.3989524046248342, -0.21359369585282476, 0.005997516325989193, 0.22245067108099054, 0.40415988065297603, 0.5321367358966993, 0.5994330582006497, 0.6125582860784616, 0.5882020176199577, 0.544529318816118, 0.49231675503003663, 0.4401080334293313, 0.39556015887532686, 0.3558701240596112, 0.30970824017613785, 0.24857457647014602, 0.1738394253110725, 0.09555506328839358, 0.025534899109909814, -0.03004705897489837, -0.0705201481681664, -0.09618878203632261, -0.10470886359376541, -0.09130786598400292, -0.054002600404003544, -0.15783595712936418, -0.2941233810182549, -0.39122688033619735, -0.43800286592498316, -0.42965865257849994, -0.3663415389995347, -0.2533227748994779, -0.10505068755929936, 0.051808048134155085, 0.19039938107932838, 0.299167558945845, 0.3778110562186029, 0.42377415708038485, 0.4282957402820485, 0.3839185905060825, 0.2974419242629895, 0.19293958313754536, 0.08856635477620303, -0.010884471119015391, -0.09954324556767016, -0.16693859750971285, -0.19631139809998047, -0.17294018901024555, -0.09169226359903297, 0.041719623073022995, 0.20739886661406, 0.37913399247999896, 0.532533635305912, 0.6491971619116018, 0.7192089134988653, 0.7449364894933848, 0.7347829353818998, 0.698079597737726, 0.6435012170440109, 0.5837046244633369, 0.5259310409822944, 0.46567559654818813, 0.3946251042809745, 0.31256120788459624, 0.22877799343125232, 0.15283766607227303, 0.0894727488193576, 0.038973354830617646, -0.0013077929134475586, -0.032964594373316156, -0.05257683991455991, -0.0539863361285237, -0.03446301687217896, -0.13380912692536454, -0.2473388257713465, -0.32310467345305277, -0.348758345302588, -0.32093029471466306, -0.2447556537923025, -0.12780347244841764, 0.020574678382913672, 0.1821986757218053, 0.33217717072075786, 0.45365660201535374, 0.5422391356592026, 0.5986609203083512, 0.6207679386461217, 0.6013276167249213, 0.5400271824970111, 0.45443193961517037, 0.367235875083968, 0.28921679357611957, 0.22591533141774636, 0.1824688879760629, 0.16569962635981408, 0.1843683121422822, 0.24151780413520985, 0.33577221122321715, 0.45610918131412453, 0.5855585134795215, 0.7070339583599257, 0.8048712426926092, 0.8689432006873652, 0.8954217040248168, 0.8843480459875488, 0.8404534837249725, 0.7740427138706273, 0.6987012396827504, 0.618604867743495, 0.530523554110999, 0.4338632878714894, 0.3379052454559164, 0.2544883424803313, 0.18740138327893036, 0.1337135518010872, 0.08869969716051267, 0.0481404628005962, 0.011971800699356126, -0.014559064262820016, -0.025680596829924584, -0.01922830151577826, -0.10339653527439654, -0.1892000552600284, -0.24166189593362514, -0.24740382169569347, -0.2019171245687779, -0.11312934694462569, 0.007586851478600292, 0.15178332450495807, 0.30870712879750845, 0.4611751597975481, 0.5923610828386826, 0.6927228341127236, 0.7589955134394155, 0.7920101845975018, 0.7898501562775337, 0.7498460870046189, 0.6830132277065994, 0.6116392064263584, 0.551466531040479, 0.5085679487385923, 0.4865450853113983, 0.48549144469182187, 0.50811455118303, 0.5550364448328703, 0.626107941520474, 0.715718761336069, 0.8130290101705929, 0.9060499023923759, 0.9816002349544266, 1.0293735097394903, 1.0408858808917765, 1.0140604009566685, 0.9528611856827669, 0.8688477582531997, 0.7723231839567444, 0.6651028885669862, 0.5498907862978979, 0.43646139331890293, 0.3381919465818175, 0.2617346000622728, 0.20441081342114717, 0.15887448747849248, 0.11735414892638757, 0.07556879797953206, 0.03612513886903863, 0.005967444774210831, -0.009931621882180122, -0.01048328877251538, -0.0690693192667095, -0.12336599186292596, -0.150346208901888, -0.13803311862183054, -0.07978085279063749, 0.01775801550284207, 0.14070693966201442, 0.27865417808658133, 0.42401913368104027, 0.5675546329144866, 0.6982030472414326, 0.8057395570498835, 0.8822530685064331, 0.9250139194828396, 0.9353061371435741, 0.912739845563789, 0.8634381287973648, 0.8060075594490532, 0.7591759140456747, 0.73120762301182, 0.7251027953227951, 0.739101956842201, 0.7706126858647794, 0.8180769396716453, 0.8795098998356309, 0.9509857972496529, 1.0243950608226426, 1.0902355482632313, 1.1384129815931372, 1.1594395311936225, 1.1461726345397245, 1.0978013762712981, 1.0180544436748378, 0.9164407313585048, 0.7982804365122684, 0.6678393215711149, 0.5364828013217499, 0.4194685138827873, 0.32640859403540384, 0.2575279733679579, 0.20716927951754835, 0.16622990233149865, 0.12597152044382068, 0.08325444887312723, 0.04244886568001246, 0.011244620971932576, -0.005594657059190657, -0.007790956175873022, -0.033334941314564034, -0.055409968877382774, -0.05690449273031084, -0.028821984319540122, 0.035939256195756275, 0.135129572390171, 0.2566118453273334, 0.38733109230851503, 0.5187864156698788, 0.6460057362817365, 0.7644308995313033, 0.8675268592609892, 0.9470420160543299, 0.9967890982085206, 1.0162641631942944, 1.0074047784966804, 0.9744873381961281, 0.9306573756218455, 0.8942334252952069, 0.876888518515275, 0.8820272293229092, 0.9081606089574238, 0.9496926619087749, 1.002120815373431, 1.0603928989019238, 1.1197229635125214, 1.1731164079232572, 1.2131929285287113, 1.2332994463520515, 1.2267939617462222, 1.1901650142582845, 1.1228339640148153, 1.027895076103087, 0.9112653904255646, 0.7781633934938738, 0.6384226513817806, 0.5063153694680361, 0.39420437846942846, 0.3072038262367402, 0.24428192398902365, 0.1989436447153631, 0.16063074618321685, 0.12127334593153712, 0.07939388329448081, 0.03946999318559719, 0.00884740923731301, -0.007217007423775382, -0.00844025967598499, -0.00048335647055859334, 0.00593362122234621, 0.026216289966160506, 0.06717533365147203, 0.1341640057726722, 0.22772008527282803, 0.3408334040807915, 0.4614278594634119, 0.5790913766941048, 0.6895186921156903, 0.7912730661072951, 0.8810496073217167, 0.953510009931636, 1.0028192982342083, 1.0257009668918138, 1.0233184275180793, 1.0005833257892542, 0.9672181275642551, 0.9387772918639401, 0.9288891459990404, 0.9423649228015114, 0.9775204599320486, 1.027827211186594, 1.0854250536819046, 1.1429303579913546, 1.1939693545117671, 1.2325022107350057, 1.2526357533752628, 1.2502784616553615, 1.2220245682077404, 1.1667150678166334, 1.0844423581833995, 0.9785689668047413, 0.8545739174469293, 0.7208477907059814, 0.5879396650986936, 0.465379357501503, 0.3606487935143865, 0.2792020767931438, 0.22225460545873102, 0.18236982840404714, 0.14776854656247373, 0.11148476475799313, 0.07288976268724019, 0.03554673961079114, 0.006175734262604882, -0.009088166710189896, -0.00933449220837003, 0.024901137463346767, 0.05220038678515038, 0.08719947062349752, 0.13629800577547893, 0.20308940308935922, 0.287503143910003, 0.3858535098535694, 0.4901874263176443, 0.5916013309836331, 0.6859623267140093, 0.7723521475656316, 0.8479191206729098, 0.9093100709074854, 0.9527090067772385, 0.9734809216940336, 0.9707778778022637, 0.9499565186878297, 0.920827902680411, 0.896773398321894, 0.8914830919833456, 0.9106238080902644, 0.9519191223310729, 1.0082374169917725, 1.0696652942508986, 1.126840948738897, 1.1724289163645738, 1.2005287034028682, 1.2060521824610209, 1.1866563287650125, 1.14212612192336, 1.0736266259863207, 0.9833291849182455, 0.8757693820271624, 0.7572603590997438, 0.6357912862214666, 0.5180106828643603, 0.4088294583443283, 0.31408404214320496, 0.24086378443667328, 0.19149983313487673, 0.1585976796139601, 0.13075594521797432, 0.1010646222826715, 0.06817384591208119, 0.034702253163400316, 0.007166941353324869, -0.007597948192065441, -0.00821578445451553, 0.039963517506881104, 0.07879784984258137, 0.11990168661132099, 0.16983558685112932, 0.2321416932952479, 0.30572809290220576, 0.38717801287255027, 0.47129112696116277, 0.5528562278903254, 0.6296207165069327, 0.7007328072927558, 0.7632021597989777, 0.8138001077497922, 0.8496822959213457, 0.8658360704960757, 0.8602529856044686, 0.8380187701791331, 0.8093536740282171, 0.7869386307893298, 0.7836491768632468, 0.8052155608159944, 0.8486664080501374, 0.9063546353337832, 0.9677803537699083, 1.022349474054431, 1.0622400181715967, 1.0813381274345855, 1.075575331896722, 1.0445019282668757, 0.9912461889756314, 0.919155526303351, 0.8319674591713601, 0.734398630749553, 0.6314558772844386, 0.5278340943867763, 0.42745696571131225, 0.3345152665735043, 0.2545308390006257, 0.1932941791102151, 0.15286006681732414, 0.1281686335600236, 0.10949534387745136, 0.08882823506471525, 0.06336092227746648, 0.03522608918860664, 0.010768561410498994, -0.0032184132312600942, -0.005249699839086967, 0.043146220365219055, 0.0837796544277603, 0.12304447116197247, 0.16640555112995428, 0.21810535957137986, 0.27756333757796897, 0.3414743325926623, 0.4055774107029997, 0.46677426453153475, 0.5247372768734577, 0.5790287096646645, 0.6272053621763654, 0.6663600444698974, 0.6935908085702401, 0.704306434426144, 0.6964564535760328, 0.67457613497834, 0.6474252639858212, 0.6266512368748498, 0.6239201144532354, 0.6445318779059233, 0.6849420882862165, 0.737575025166341, 0.7925922764605402, 0.8399829502185225, 0.8721317257581952, 0.8836155215350946, 0.8715429028827486, 0.8374334457473896, 0.7861240003123396, 0.7214728212324931, 0.6471977478752362, 0.5673012735781824, 0.48503616013908213, 0.40253228680824804, 0.3225746909134947, 0.24944198325477457, 0.1874518275299167, 0.14008336288328008, 0.10951713793115786, 0.09337832201101333, 0.08355129009455262, 0.07155918607866754, 0.05392424412042569, 0.03243395963681916, 0.012651136387072676, 0.0005295885595437582, -0.002482544256361462, 0.03512920651755234, 0.0682126096758165, 0.0990306223505097, 0.13077792734969235, 0.16723128250450292, 0.20880841949775578, 0.25319306261261615, 0.29735122949583914, 0.3389720942592667, 0.3780261561393355, 0.4145407908651096, 0.4468635457806213, 0.4731618749418718, 0.49091083379091593, 0.49658877953480574, 0.4888554737751433, 0.4710599668288106, 0.4493216071235785, 0.4325628870239699, 0.43030745279326277, 0.4466761374487947, 0.47832176874712806, 0.518689057529841, 0.5601377393311273, 0.5950366920330492, 0.6175186155953226, 0.623737235161935, 0.6119370743405529, 0.5842556938841443, 0.5446873337217593, 0.496122041714835, 0.4412530852394925, 0.3836237421160985, 0.32583945071441156, 0.2685978021489784, 0.21316376062394732, 0.16247350418325898, 0.11951590403055258, 0.08697867328308947, 0.06716307026453966, 0.058695320561815395, 0.05503658757142498, 0.04928236516174745, 0.038662346190099554, 0.02443830597184102, 0.010615777743799137, 0.0016786411438374483, -0.001062793980924478, 0.01931883663852062, 0.03767067983754794, 0.0546969886655027, 0.07159787759436673, 0.09041351133625915, 0.11176676410967169, 0.13448423419064306, 0.15716052540826958, 0.1785292204683099, 0.19831867086964655, 0.21666577314716984, 0.23273292406666768, 0.24574964709648273, 0.254343213402917, 0.2565298863926259, 0.25179389079542985, 0.24179450868963945, 0.22965330706372164, 0.22013818584079287, 0.21882132127666937, 0.22796536951099394, 0.24549428792440994, 0.2673795017480763, 0.2895329475232899, 0.307880535565878, 0.3194166488174252, 0.3221626007073573, 0.3153648673907629, 0.3003265434546142, 0.2790014952162897, 0.2527965260541944, 0.22310682515769328, 0.192432522022922, 0.16257636957149235, 0.1335198548657718, 0.1052704868797587, 0.07903894535844808, 0.05663991020488699, 0.040047638192783966, 0.030725362050584612, 0.027642931842916645, 0.026917485861513685, 0.02482256358704042, 0.019958795528361148, 0.01296196664401296, 0.005866911069672442, 0.0011124468868017462, -0.0004516377590053124, 5.588183339936756, 0.007279414516608228, 0.01576046073618965, 0.02754238609139368, 0.043227066089402126, 0.06019830428707712, 0.07559444751785674, 0.08951276350744551, 0.10294249056460968, 0.11548824980731547, 0.12689374517986923, 0.13714196184793925, 0.14544857644713108, 0.1502216999457052, 0.14991942579027154, 0.14406928502503563, 0.132430024391535, 0.11545868860090895, 0.09496080937022253, 0.07306355785091138, 0.05067543637941472, 0.0275775923203267, 0.00217720217792809, -0.02657198953920521, -0.05734665077129361, -0.08856111013522146, -0.12072322331712218, -0.1548616759004495, -0.18986087876971106, -0.22270412761015038, -0.24965912514467611, -0.2690528953279944, -0.2838360238428966, -0.2975034689055267, -0.3098674556643694, -0.31906984398604626, -0.32404439247449324, -0.32308995905700777, -0.3135094830896676, -0.2945846013387076, -0.26823692931547205, -0.23758063416024022, -0.20661805672603112, -0.1778023989047795, -0.14989730592547215, -0.12025095084533902, -0.0886435446753111, -0.05729829339636838, -0.027880528802613, 0.010551482504638247, 0.025345297465624358, 0.04746318071898408, 0.07679541874646993, 0.10869656032819232, 0.13826462898264627, 0.16492062444296118, 0.18957345199368833, 0.21234587788444634, 0.23361301185557568, 0.2528935605538267, 0.2682568713593173, 0.2765739950320156, 0.27499031810914054, 0.2618081159869725, 0.23576620722087532, 0.19816936316093514, 0.15446496885289432, 0.11099981438161227, 0.070994936146034, 0.0339194327557979, -0.004946151342560594, -0.050681367755038224, -0.10394854252698629, -0.1633321985939394, -0.22897748855738376, -0.30044500633709803, -0.3741052087171557, -0.4436321695608286, -0.5014326263028659, -0.5434638267924625, -0.5741935707800042, -0.6003975111675783, -0.6227399511610032, -0.6382569663399383, -0.6449658923158061, -0.6402646928438182, -0.6203002455349801, -0.5842052067914146, -0.5350746923935055, -0.47759817466464816, -0.4176811804972791, -0.3596132261281049, -0.30223573997977, -0.24175733031398228, -0.17811286263576165, -0.11533899645690407, -0.05628074327025297, 0.008579049658241177, 0.025680779452170573, 0.05407863683867781, 0.09174342006997195, 0.1331850048769516, 0.17289509106008008, 0.20867026113402742, 0.2404503126559972, 0.2701031907028381, 0.29974768984404815, 0.32821149347851525, 0.3514457959653432, 0.3643562389875444, 0.36226615598747725, 0.3406312411388748, 0.29637133243418484, 0.23243803207800048, 0.16005755200308971, 0.09257591928160651, 0.03817506080595195, -0.0027941126665145593, -0.03925543534454304, -0.08446596362968406, -0.14642990076010035, -0.2272798264735861, -0.32638690029191514, -0.43866364691513565, -0.5547712041282512, -0.6640004410005061, -0.7554483479919412, -0.8228450195822506, -0.8704381929874753, -0.907240282374816, -0.9357470017768226, -0.9530347893430506, -0.9568027609933409, -0.9447297996901595, -0.913854970092581, -0.8637303930639213, -0.7971238513365929, -0.7181305020692493, -0.6323285884108016, -0.5450501475805974, -0.4568389364328627, -0.36473530926710757, -0.2691580319859125, -0.17510876252246027, -0.08587106309035286, 0.0013355714886213528, 0.01426773795934628, 0.04141568231095983, 0.07957168704617681, 0.12356286056766248, 0.1678141647535028, 0.20806940681775943, 0.24345461186568135, 0.2781077016257307, 0.3161395652122169, 0.35541540256721516, 0.38898654217314643, 0.40949634202968666, 0.4092183410291541, 0.37928189826471254, 0.31445307301362646, 0.2195294068958375, 0.11196194761481783, 0.013935548162900383, -0.05808577433066605, -0.09971515407570936, -0.1230294736079732, -0.15210495398772422, -0.20743494434773416, -0.29875629756085703, -0.4256992277463845, -0.5771644198997901, -0.7350490706583563, -0.8821303303631782, -1.0047842954456192, -1.0958840576174445, -1.1591208081565803, -1.2043800605596862, -1.235995795743866, -1.2518392726586174, -1.2498609508678373, -1.2288780972229956, -1.1879268660258109, -1.1272140801002453, -1.0478556243817518, -0.9518463878813068, -0.8437026635666537, -0.7293014404031078, -0.6110977114675538, -0.48783772070103937, -0.3609231782727689, -0.2359719559348241, -0.1162570674173737, -0.01100101941924366, -0.010326566233278095, 0.0059937678985881844, 0.036388835659091, 0.07655792731182012, 0.12014690550847965, 0.1614541271723232, 0.199599011657102, 0.23986787674837395, 0.2867745173856929, 0.33694883184043545, 0.38157410142212106, 0.4113429636951138, 0.414196582813631, 0.37656621308634347, 0.2914390443758141, 0.16434953746240538, 0.01706281647289004, -0.11925525498799162, -0.21694825903121873, -0.2640657800397227, -0.2731972652579516, -0.2783647917142491, -0.3142762028463892, -0.4013461914583095, -0.5425295675088033, -0.7225442236793824, -0.9141906766067572, -1.0918218033921077, -1.2383232787227054, -1.3466471880228095, -1.4206964016833834, -1.470888016077357, -1.5035772448980596, -1.5178804154823062, -1.511615740554252, -1.4840632161976346, -1.4355055901116485, -1.3665389381062882, -1.2769406036096742, -1.1669581525556443, -1.0404276205981708, -0.9031512938126044, -0.758133289024762, -0.6057315123350065, -0.44900135396332846, -0.294345539375634, -0.1452732139854186, -0.02749839484865126, -0.04632092155799066, -0.04965378367794063, -0.03449317022561987, -0.004011075647593341, 0.03431407861947877, 0.07441987560196485, 0.11549425889140684, 0.1617278333402159, 0.2162290012769477, 0.2750138220517946, 0.3290940205481874, 0.36700836656117825, 0.37177087425852423, 0.3266420735792169, 0.22398907334613133, 0.06838694174300858, -0.11690921136735613, -0.29351359825175427, -0.4225615465565477, -0.4833946098583219, -0.48652292217443754, -0.4711844488394114, -0.4826410820342969, -0.552402737635331, -0.690400940966004, -0.8813430292772211, -1.091866708225018, -1.2880640035213087, -1.448003190684079, -1.5642834298862733, -1.6415628017590083, -1.691065343062652, -1.7216857038454023, -1.7348790684013298, -1.727966002659549, -1.6986374891583187, -1.6461217109675106, -1.5704618952578822, -1.4716162530017676, -1.350149469541148, -1.2095573453294954, -1.0545688017713089, -0.8876461762097555, -0.7105802739790884, -0.5281182779464849, -0.34703198366290583, -0.17136595871705956, -0.04784111683114872, -0.09105900437883842, -0.11954826563508625, -0.12482137535654617, -0.10854599539799184, -0.07892125731855981, -0.04227782301809864, -0.000295378645340025, 0.048913234637297374, 0.1069922426095009, 0.16992557231802416, 0.22841027178094198, 0.26840709340183905, 0.2698515527336289, 0.2166939657689447, 0.10247291466869217, -0.0701084868255921, -0.27921879870555133, -0.48375496566202836, -0.6390254249887032, -0.7185051153440304, -0.7283342286150947, -0.7055571672552724, -0.6984880952114118, -0.7469205664234239, -0.8693962268583945, -1.054147222495913, -1.265598593830296, -1.4646647794694883, -1.6254115930202768, -1.73995305845242, -1.8136794743163935, -1.857926181857438, -1.8830037921171205, -1.89318922485413, -1.8864223444496493, -1.8582988730595202, -1.8054201828440388, -1.726131554114888, -1.6206599544696374, -1.4912065824204825, -1.3412585824239687, -1.173852430448247, -0.9909885541189983, -0.796007595147513, -0.5944799154512754, -0.39238955189023617, -0.19413554118633367, -0.07222346013855345, -0.1415378909363332, -0.19585696937908562, -0.22327135589718833, -0.22375827824556926, -0.20548632008930684, -0.17551240993967385, -0.13744539655599844, -0.09156021138467912, -0.037402204733738995, 0.01975447777919742, 0.0698075851119161, 0.0985311585405707, 0.08769285594130914, 0.026326868834317625, -0.08887804043920186, -0.2565390599701158, -0.45965551830576934, -0.6624116976559208, -0.8245672854135979, -0.919189694728062, -0.9457450342775463, -0.9314148391608639, -0.9193992418212763, -0.9524710295985769, -1.0563048348092783, -1.2241803379286673, -1.421239573492332, -1.60753132942722, -1.75663903009714, -1.8614773022935245, -1.927999297828645, -1.9662150626091766, -1.9851068159170007, -1.990035938103774, -1.9806879310771766, -1.9524936113441174, -1.9009228673088951, -1.8229476375098623, -1.7173216656810362, -1.5859685600434967, -1.432148599791008, -1.2576084717631746, -1.0644758735870619, -0.858050044655078, -0.644228690937425, -0.42739975516835177, -0.21199296615733373, -0.0990857935730954, -0.19321039477672777, -0.270522378219461, -0.31963361168172716, -0.33919828679874675, -0.335583227361403, -0.31643964342372305, -0.28862880260939955, -0.25504329629618827, -0.21774979763641364, -0.18425039086081502, -0.16261424466541832, -0.1619267689760956, -0.19375554401286668, -0.26192995012761033, -0.36469553400621757, -0.4999760517475512, -0.6587441252627235, -0.8196564608922708, -0.9574233743762108, -1.0509817711443696, -1.0937029498201947, -1.0988487751899323, -1.0968717504948795, -1.125463351354555, -1.2127814722674066, -1.3581229428324653, -1.5311363072200732, -1.69488192740128, -1.8252807744668305, -1.9166251310678928, -1.9752382501310144, -2.009132921191581, -2.024325792403774, -2.024823985128813, -2.0113090547915733, -1.9804846163660432, -1.9292098184319368, -1.8557183473672494, -1.7573751397098667, -1.6326200965291278, -1.4824184037986214, -1.307383232627528, -1.1098242597689199, -0.8970264777447504, -0.6760676152521137, -0.45035443168619754, -0.22394638521912064, -0.12586374805728498, -0.24205423709185908, -0.3388348890413045, -0.4085972078363972, -0.4486438642418129, -0.4621250545289139, -0.45839963999617434, -0.44922598878059417, -0.44109134002463224, -0.4392991030827511, -0.4507287862142407, -0.47627462506903256, -0.5161734547527312, -0.5746973004233072, -0.6490745051029518, -0.7295122146068846, -0.8099514504518563, -0.8901780024980164, -0.9696432952588061, -1.0455155112823358, -1.109192076417005, -1.1528209516017869, -1.1775481888442436, -1.1957466334622584, -1.2302685344232345, -1.3044189983415044, -1.4237608618084725, -1.567448538527494, -1.7051664551636248, -1.815959900964176, -1.8946253965965536, -1.9470912714285518, -1.979637181823659, -1.995473167324825, -1.9958928134208338, -1.9807894634349212, -1.9479553536898486, -1.8962715864791924, -1.827207188158987, -1.7395055857700212, -1.6286224665456384, -1.4912799174450821, -1.3253684796133895, -1.1318715975021651, -0.9186951506017152, -0.6949893394845296, -0.46497171417287053, -0.2321515091895098, -0.15017172674574442, -0.28571335952348204, -0.3994496278093461, -0.4873850152736737, -0.5456209786604259, -0.5769487927535196, -0.5952980587929876, -0.6169566481384297, -0.6506820329978821, -0.7017000621709815, -0.771287773124286, -0.851680127182186, -0.9363696389254165, -1.0249794812770139, -1.1075564110681093, -1.1628257721681472, -1.1787330063631778, -1.1623372623592263, -1.1340952630484367, -1.1157320792754748, -1.1160253145474566, -1.1338125676123447, -1.1648307253286871, -1.203588323497339, -1.2510952402677757, -1.31864648522444, -1.414724413094179, -1.5287516456496821, -1.6384175360682445, -1.7276353213722622, -1.7928005653493564, -1.83950798360943, -1.8731806701274607, -1.8943273324733945, -1.9004418774019982, -1.8890703575244452, -1.8587167896921624, -1.809927450895449, -1.7465841513594487, -1.6703737090038537, -1.5771037547429196, -1.460336392804027, -1.313835002851434, -1.1348376054483198, -0.9293344363989336, -0.7077633699693987, -0.47647733108379364, -0.23926564335533843, -0.16948184481409637, -0.32229237830530116, -0.451447913783275, -0.5535521591245144, -0.6270055632628487, -0.6802569815976198, -0.7316215929993404, -0.7970795308237445, -0.8826039766045127, -0.9885225672415988, -1.1101395532615523, -1.2364609714596284, -1.3600053021434229, -1.4767298394150663, -1.568164949609399, -1.6029928623489815, -1.5643909359287, -1.4626890487147437, -1.3305493113105222, -1.207349864163052, -1.1198527938470955, -1.0817778413314405, -1.093176463440693, -1.1385961692055189, -1.1986116015336035, -1.2688186492723965, -1.3527604494101735, -1.443892964776583, -1.5254283013172207, -1.5880710333333397, -1.632948411981453, -1.6666335281219324, -1.6965120066966894, -1.7224782380565389, -1.7373209372971656, -1.7348254390655147, -1.7134744259372534, -1.6747133553360283, -1.6228199168109205, -1.5614751657702284, -1.4887140064534663, -1.397282537320522, -1.2776217055000412, -1.1223178256141053, -0.9328325939698631, -0.7185371808577674, -0.48797293552340154, -0.2466671413633592, -0.18281762052800196, -0.35009934208387744, -0.4925038322969914, -0.6067262339354665, -0.6987434642353826, -0.7840863682601027, -0.8789641786503966, -0.9914458420624285, -1.1202222926960248, -1.2613634823511466, -1.4101510487208533, -1.5601894163959398, -1.7070442059158655, -1.84208181354408, -1.9415815494870816, -1.9726040834796057, -1.9149938124979125, -1.7729690112697118, -1.5754219334707424, -1.3663856621643253, -1.1872320706012722, -1.0705025988686292, -1.030027685462403, -1.052497580606794, -1.1091907651677853, -1.181847468270745, -1.2619698011081626, -1.338520820556279, -1.3965307500647004, -1.4320111247889125, -1.451295974637442, -1.4614741602533825, -1.4739687140927764, -1.494267347740988, -1.5136842695334811, -1.521689226010852, -1.5151987791334478, -1.4947543560579812, -1.4625118129324681, -1.4223395719032426, -1.3746422311112276, -1.3124318388003373, -1.2241819973813457, -1.099054584951523, -0.9328574055060473, -0.7307273209998758, -0.502036230875354, -0.2555880198544351, -0.19101358198030852, -0.3686907520719008, -0.5223090539690619, -0.651672961089468, -0.7711120750946834, -0.8969087560334673, -1.0345015315311041, -1.1801258197514897, -1.3278374109434636, -1.4749745879139724, -1.621492611553205, -1.7694470334380434, -1.918846103774835, -2.059147500443257, -2.169765521973778, -2.2238328073602798, -2.19628463613515, -2.0739898859029995, -1.8681895033228724, -1.6161470456959022, -1.3661628880373282, -1.1669366102622096, -1.0506554557735486, -1.0166356450682927, -1.0402215856208048, -1.0956036178553226, -1.162025275475454, -1.2204108618372846, -1.2557128513864022, -1.266129370347195, -1.2606511862488343, -1.2452345762000692, -1.2316213199715333, -1.2335434959435907, -1.2482741024673747, -1.263835679768412, -1.2742371606646923, -1.2779393994908173, -1.2733692712902958, -1.2619914274876582, -1.245243888593649, -1.2164607423164753, -1.1624693321486126, -1.0703823490412794, -0.9314704618521609, -0.745049687545335, -0.5191733347573131, -0.2663459480428819, -0.19607460794281106, -0.3815846322702772, -0.5474117450524455, -0.6981514381409437, -0.8513184500910649, -1.0148757360684304, -1.1797908737792875, -1.3351127746525866, -1.4769380259341731, -1.6057743328133314, -1.725869254865797, -1.8483895746656613, -1.9800492701737642, -2.1143948520791556, -2.240954013471999, -2.341490857961106, -2.38418641916294, -2.3341828026353095, -2.1793130512308148, -1.9398092539559872, -1.6583275515690519, -1.393131709577334, -1.1944657626043742, -1.081211269032466, -1.041694591132244, -1.050885818234254, -1.080158293465674, -1.1035018330320583, -1.1045903270902233, -1.0822290826878669, -1.048025655808192, -1.0098220734278722, -0.974680651951742, -0.9568168906253616, -0.9616109425380733, -0.9812121126065411, -1.007638963856175, -1.037430695605861, -1.0665363383551232, -1.0917320098952228, -1.1119799773901669, -1.1198731098436312, -1.1006334973785363, -1.0400373307200337, -0.9271368579510304, -0.7569817785338271, -0.5352595516681574, -0.27684578059444265, -0.20096654715552612, -0.3950746614473373, -0.5770726246501239, -0.7547326493494141, -0.9406756941573672, -1.128618774768626, -1.2991255991767572, -1.44219890098342, -1.5587844296646223, -1.650990624541621, -1.7272077994500623, -1.8087583287536193, -1.9105916699458159, -2.0336266901010958, -2.179546662100219, -2.33906808500215, -2.4750576069630466, -2.534013531637926, -2.4784829825258257, -2.3003900921810083, -2.026646142012306, -1.7169612810504045, -1.4366019142593602, -1.2283438100051358, -1.1023748304261383, -1.0429697596645349, -1.0185319343788928, -0.9960196378569379, -0.9535399899086611, -0.8869102241545861, -0.8118819812638586, -0.7466222690974684, -0.6970948030832516, -0.6687916271213447, -0.6678334531161927, -0.6917482062921322, -0.733577547368243, -0.7894494275062552, -0.8551538185975579, -0.92249638547966, -0.9840295239032535, -1.029569390121494, -1.0429568892360248, -1.0092526854371202, -0.9178621162596854, -0.7624924896606367, -0.5464858265666322, -0.28502174631732746, -0.20779492376216904, -0.4134801818615664, -0.6161734332143433, -0.8223404755407787, -1.0327643076131334, -1.2273935969074745, -1.3834885453471262, -1.4962239239996649, -1.5713330986393632, -1.6141205860665127, -1.6410690992168402, -1.683219850195988, -1.7598000126223778, -1.8766930882956134, -2.045644549984254, -2.266563583981556, -2.4999819653876183, -2.6790187582935934, -2.74010849677186, -2.6438101911982432, -2.399379615793388, -2.0593045267021037, -1.6978056921259461, -1.3827103908961915, -1.153933128455293, -1.0135968575203504, -0.9326126013174735, -0.870953952006899, -0.7949393221349015, -0.6901312995933705, -0.5719769911295884, -0.47266243675751146, -0.40756321809363744, -0.375551392101643, -0.3772824019239719, -0.41084354497379166, -0.4694043184301318, -0.5501571707393795, -0.6512780024126493, -0.7613287311960526, -0.8644956431588378, -0.9459309740636268, -0.9884855399216097, -0.9770748740962738, -0.9028655120523662, -0.7606945764725954, -0.5519993252076829, -0.2903760202670205, -0.21759145956839118, -0.4383994829880242, -0.6637814867841308, -0.8940925685830603, -1.1168762423743843, -1.3031989719415045, -1.4314140154205346, -1.5017297379981485, -1.5252393732701834, -1.5166681360367777, -1.505306116803158, -1.526929658344872, -1.5967051699340638, -1.7194513205705662, -1.913412591926024, -2.1843351036273937, -2.4926148620671476, -2.766952656148501, -2.925230797624728, -2.904384946118834, -2.694479920020672, -2.3326513513975886, -1.8942639968646167, -1.4695079010817549, -1.1318200966281242, -0.9094041594800422, -0.7806368696687519, -0.6997984519453456, -0.6172375474058933, -0.5007480515895045, -0.35621609322489817, -0.22397515488376887, -0.13593432892899712, -0.09613074995326061, -0.10244938154275647, -0.15028556537591822, -0.2283736451047831, -0.3321798016886494, -0.4630907433910386, -0.6099798493514498, -0.750196992871248, -0.8630940154380018, -0.9304375387850903, -0.9376203686760751, -0.8778598637028066, -0.7481257719071516, -0.5486807198826016, -0.29090114335905787, -0.229673726866963, -0.4667258218839572, -0.7120935021522624, -0.9584059489747405, -1.183324227200774, -1.354659379582798, -1.4527074466241277, -1.4800618753528847, -1.4551117502039772, -1.407104929026135, -1.3772707404339195, -1.3997588913223131, -1.4795756856421172, -1.6180396663792056, -1.8330102355734168, -2.125901930195044, -2.461984971450207, -2.779367776567513, -2.9924085156160656, -3.023308939563443, -2.8409049177977233, -2.4627512162734093, -1.9573126706745592, -1.4299912116887867, -0.9914405506532227, -0.7022336972319522, -0.5507151986943689, -0.48278402417191696, -0.4314389422337945, -0.34081283779204935, -0.19694287290050566, -0.03980158531788436, 0.08037743905785748, 0.1410985751600569, 0.1389844558290491, 0.08081569028155797, -0.0155495514524946, -0.13955316792360534, -0.2925710613127815, -0.4658542903429093, -0.6342418098821728, -0.7720856666203731, -0.859358810145774, -0.882030268626298, -0.8353231366647761, -0.7185263270675196, -0.5314916651358571, -0.28355830062241877, -0.24001580956583726, -0.4898450973103569, -0.7483708485557968, -1.0016096531941354, -1.2230685726151869, -1.3821249068728283, -1.4596768166190142, -1.4578578973150513, -1.402143316735075, -1.3344188887766306, -1.3021760703547243, -1.334218382142611, -1.4286062106946862, -1.583340111324714, -1.8038079342674447, -2.080083989573912, -2.387801999051271, -2.685468725921095, -2.899667215638932, -2.950231651654398, -2.7881507990725547, -2.4052825341778084, -1.8493448134546748, -1.235648940422018, -0.7149928110868058, -0.38731873393951705, -0.2531849197633555, -0.24083090298557722, -0.261441959814873, -0.23523432910008724, -0.12113043547116882, 0.05020411416353849, 0.21152664417741135, 0.3116657585441011, 0.3312864678387502, 0.2760580766987358, 0.1696586529514523, 0.031237546474500572, -0.1359351594354146, -0.3244171719588748, -0.5101313666679241, -0.6651448850135039, -0.7678274826954707, -0.8043571420517764, -0.7711426704870273, -0.6692654712562165, -0.4987931380949708, -0.2675383760882179, -0.24467373763623038, -0.5001003209332119, -0.762773564820941, -1.0151220991514438, -1.231749622588448, -1.3863955262245737, -1.460036605407422, -1.4524084805992872, -1.391371283319658, -1.3233645423597298, -1.294893493896111, -1.3314770943089493, -1.431664158557183, -1.5865035405088386, -1.7828497647703672, -2.0016790774327333, -2.2301577067142406, -2.451369400643058, -2.616561381934929, -2.6587490837817636, -2.51884781802942, -2.1575627854448927, -1.5904755542623383, -0.9302299808768256, -0.3578372735044735, -0.015622433574000021, 0.07572675540933543, 0.002999625362978545, -0.11919404347313982, -0.18531189179254948, -0.12540582911357956, 0.04589839827352392, 0.24955710305464007, 0.4042900585350763, 0.46574375311440663, 0.4323674795243411, 0.3300361590957793, 0.18625873295133077, 0.013030507423779564, -0.1806836320144209, -0.3735665650124344, -0.5383676557265508, -0.6528096170820812, -0.7028226585423616, -0.6849191929140398, -0.6010099050626254, -0.4516022250271046, -0.24352197899577402, -0.24233414734178985, -0.4953258577513529, -0.7539331506406171, -1.0000837337355626, -1.2129901426977747, -1.372625209849702, -1.459905489681899, -1.47030467446418, -1.4278954012100202, -1.3738461617466349, -1.349104598050125, -1.3789512849043786, -1.4627851747617058, -1.5834793085809444, -1.71687696933641, -1.8418616773796364, -1.9535645843728873, -2.057365102767867, -2.1370112506685857, -2.1521525877398853, -2.0501854264596604, -1.768108731451622, -1.2794184465379608, -0.6613482369249435, -0.09705695905547711, 0.24438829065333678, 0.3166765202252, 0.19439259469390766, -0.006255983217171145, -0.15952464574028694, -0.16410634519172268, -0.009884719618127742, 0.2221814295200953, 0.4301008749172661, 0.544142276166009, 0.5487522645515355, 0.46670889215992284, 0.3303909333010925, 0.16047364637922534, -0.030267933949563258, -0.22266054267506197, -0.3917717367661063, -0.5155997354429789, -0.5792981350501775, -0.5783962419358729, -0.5150488844320459, -0.3907748305360254, -0.21197314813884666, -0.23368944288757254, -0.4773467921722661, -0.7254603319080335, -0.9623499962138629, -1.174243601630266, -1.3477786106561338, -1.46358373696598, -1.5107650376204371, -1.50360791702822, -1.4718588573979348, -1.448254527317827, -1.456188975894787, -1.4943004237060382, -1.5415741047629157, -1.5744156314141269, -1.5747051224963118, -1.5423209228230206, -1.50422597727545, -1.4807969711595448, -1.4728130905112526, -1.4493488911049173, -1.3260363740255035, -1.0257700899405824, -0.5678557792557803, -0.09893511134453742, 0.2178489467112414, 0.3183095068008251, 0.2347305858999582, 0.04603350617619486, -0.13332639469982388, -0.18388050474845039, -0.06007479830220324, 0.17595960248957956, 0.41752633556978996, 0.5790020904880872, 0.6291178883139319, 0.581256498647691, 0.46682586385805563, 0.3111401271021633, 0.13021646889560565, -0.057260320344874244, -0.22783716462684986, -0.35985907905170944, -0.43746706635396987, -0.4547451425508271, -0.41407117132699267, -0.31842680319798383, -0.17412226697265176, -0.2212430230839096, -0.45098197906508386, -0.6842886249874374, -0.909970218409264, -1.1225987970658327, -1.3159876773668668, -1.470437149649441, -1.5662429646203482, -1.6036894361546263, -1.597780250038176, -1.5713059131042522, -1.5444629865758535, -1.5141229539824752, -1.4588237294171886, -1.3624604169888461, -1.214577416428628, -1.0241048979952494, -0.8381249538816166, -0.7130535027123377, -0.7022218400136376, -0.8001030644218313, -0.8949148262874193, -0.848911218196474, -0.6262906634852237, -0.3245177145188128, -0.06970565119836052, 0.07455186835914529, 0.09642033904749739, 0.01718912757792874, -0.10200971114538235, -0.15632620414349543, -0.0673666345556717, 0.14583720696449087, 0.3940674493132826, 0.5877922959290734, 0.6826453816480187, 0.6786504778367285, 0.5994914838972921, 0.46875507176486214, 0.303536218769111, 0.12376353410173425, -0.04664849151962006, -0.1860500880073368, -0.27783959578055967, -0.3149073951495158, -0.2998527506380445, -0.23684579788895604, -0.13159410973932778, -0.2086222076077434, -0.42328456685326515, -0.639408592104436, -0.8513015716588832, -1.0631128418225193, -1.2764130080371348, -1.4721538607908164, -1.6221015539841566, -1.7100425766613012, -1.733783306184653, -1.7051467163530274, -1.6391459425300614, -1.5308355231507842, -1.3616777026306506, -1.126008105103365, -0.82570744570404, -0.4804079551844047, -0.15347475554271775, 0.059087757455437276, 0.047462146967070316, -0.20233836285987553, -0.5304450717166667, -0.7462501531941352, -0.7708781885855255, -0.6511520034822533, -0.47423934664070794, -0.2992005246194049, -0.16332025548114368, -0.0845883898870629, -0.07734971806634941, -0.09309824922483785, -0.03328660489623351, 0.14010189427659317, 0.3745131593447293, 0.5864452978571573, 0.7220560254928938, 0.7666450349796423, 0.7317410707440759, 0.6344000323115137, 0.49021274092796224, 0.3210424607698263, 0.1527859650371098, 0.007271547450230422, -0.09885272314879456, -0.15792024338706942, -0.17248614928043607, -0.14683700941688818, -0.08507931819068, -0.1982233504109826, -0.3987805911723369, -0.596610470355423, -0.7911394574959891, -0.9961501228401768, -1.2224941767198347, -1.4548207586304174, -1.6587326086359573, -1.8018141726604833, -1.8628296089406158, -1.8396714216797576, -1.7412855328255528, -1.5632898221221374, -1.2928150683105555, -0.9358103531890523, -0.5070791563441623, -0.034865174682986104, 0.4015995774966862, 0.672272916351622, 0.6281548319314597, 0.23800074531749385, -0.29326164476396516, -0.7342136127383384, -0.9731450226438818, -1.0146690793301427, -0.9136624974780986, -0.721317661452909, -0.4857357794654562, -0.25118240614750215, -0.095820013452067, -0.04540161503879427, 0.005312586920688812, 0.14509016092549004, 0.3632439962890566, 0.5873953105541879, 0.759325417059232, 0.8529018515948854, 0.8659852416273978, 0.8064549936064201, 0.6870852757014391, 0.5315104403587199, 0.3676284679998541, 0.2172649055634199, 0.09668919507137318, 0.013789432494229667, -0.03368729439713932, -0.049217864112600734, -0.034753757282887696, -0.19036367273717542, -0.3784819066939549, -0.557454672812599, -0.7303726738395274, -0.9200484835432674, -1.1475576756456123, -1.4044164875781682, -1.6550133512659388, -1.8541789686444543, -1.9618527213167027, -1.9603657194531754, -1.850921672455836, -1.6305929859921355, -1.2949269680239477, -0.8613704060187, -0.35703137026449755, 0.1809824649331646, 0.6658112344923455, 0.9559520885592825, 0.8935984804501023, 0.4334190701057233, -0.22134538058899264, -0.817191000112094, -1.2110874300565417, -1.3748161001623638, -1.335098374115707, -1.134656620527884, -0.8293165883375795, -0.4823852507129198, -0.20640254334935368, -0.07974495379006136, -0.001680926201410789, 0.13948889491956806, 0.3590609334188458, 0.5987055368578036, 0.8042763570345701, 0.9437169781437668, 1.003121829678611, 0.9814803341916722, 0.8884696709234025, 0.7486768691340062, 0.5910952771075395, 0.4371845837263979, 0.3025710592358792, 0.19494987556545368, 0.11264605848200744, 0.05380145490037564, 0.018585296285656083, -0.18401354985982998, -0.3607648921608035, -0.5207284935352162, -0.6686426595218093, -0.8341949776861176, -1.0487832377327355, -1.3135924286906364, -1.5965445679357928, -1.846172499026385, -2.0082479830123647, -2.049068295536288, -1.9600382530936493, -1.7393496788996679, -1.3912215146315683, -0.9438103317267105, -0.43385072381720524, 0.09810563442407698, 0.5699924643108948, 0.8523902701598294, 0.8005369064887227, 0.36379234288602164, -0.3001429440546772, -0.9486216985615045, -1.42015500229485, -1.6562817844985664, -1.6599145952961418, -1.4671912777552516, -1.139807866841511, -0.7519710509601361, -0.4174387172137044, -0.2174736315999417, -0.07238540796730857, 0.11429162986481005, 0.3605736126158684, 0.6231617992707069, 0.8607281737783128, 1.040727916437539, 1.1404562960019458, 1.1526310387256407, 1.085286222975633, 0.9629937928151959, 0.8141352779476656, 0.6588678828364677, 0.511453004697627, 0.37887612036764917, 0.26065136213121876, 0.15772689229112805, 0.07245863587574601, -0.17598071018873226, -0.3408454876121129, -0.4822975957043896, -0.6043817859293007, -0.7402874321889013, -0.9297787126604996, -1.1848227396322273, -1.481346934529784, -1.7688449605774184, -1.9866083255307174, -2.088793469926382, -2.054813991577096, -1.8801865064174013, -1.5753317285572581, -1.17419853204385, -0.7160979167206839, -0.2419882113161446, 0.1741375875932973, 0.42810147935544884, 0.4074140971437206, 0.0659814969646263, -0.4961080621479225, -1.0846029692560246, -1.544500804931077, -1.797267072274561, -1.8270280060090602, -1.6627480269822024, -1.3644760482275347, -1.0010912196968949, -0.6597460480390143, -0.39686312629247666, -0.16703739178587407, 0.08756854464774476, 0.3736704130976017, 0.6631370533873256, 0.9292353350924931, 1.1403160590605042, 1.269479472445869, 1.3082165838977444, 1.2645342659988639, 1.1613358149976396, 1.0241031916731886, 0.8703381891821715, 0.7120279531734446, 0.555071746426626, 0.4011465347216321, 0.2554377531702111, 0.1228503173697341, -0.16311251866231025, -0.31385521544630446, -0.43837258440616755, -0.5378266065862393, -0.6437172579250485, -0.8001465748529641, -1.0297484559488195, -1.3198574218383035, -1.627321445632191, -1.8928971758486535, -2.064367061613973, -2.1105202385131325, -2.020470743518029, -1.8039453206067375, -1.4939787988677855, -1.1258456346715362, -0.7346511654656411, -0.38626912947806635, -0.16420657095348112, -0.14713164772046264, -0.3707005975099768, -0.7744014350359997, -1.2217103018664233, -1.5880480433769442, -1.7987722772036183, -1.8322118491519406, -1.705689215387197, -1.463005691039741, -1.1535258825245427, -0.8279651506746233, -0.5208960274284489, -0.22097887469774155, 0.09113786769312697, 0.41071944230424623, 0.7217313907154468, 1.0065525081480036, 1.2341359256451294, 1.3789808081507853, 1.4358670906147504, 1.4131921482554057, 1.330153831937832, 1.206946394649702, 1.057008500904104, 0.8898537269005036, 0.7107959612905795, 0.5244768348756801, 0.3406868130665836, 0.16667779028913315, -0.14573531465609954, -0.2803615851598911, -0.39017071871379294, -0.4725966764339215, -0.5529991897480571, -0.6739279150628145, -0.8657659802155242, -1.1297929568093636, -1.4356456830803948, -1.7319639605299142, -1.9669820741391844, -2.1021970932654686, -2.1181176733883507, -2.0168427275404697, -1.8220642930051816, -1.5637294641964141, -1.2706138333588466, -0.9950164208234533, -0.8036959288262095, -0.7510491911419538, -0.861147595933643, -1.096556432284815, -1.3665156105033807, -1.582771816156181, -1.6976872427869922, -1.7020598477726885, -1.6007649154915153, -1.4110536827032494, -1.1549771765320784, -0.8543789030392845, -0.5325996674709602, -0.19973557146750967, 0.13913973442720948, 0.4735333218377347, 0.7930831713208047, 1.0809615640533303, 1.3082435048724648, 1.4566076025847177, 1.5251406575881208, 1.5208605166871707, 1.4577720241670744, 1.3494924160723185, 1.204783028033389, 1.0311905073531735, 0.8345582592419888, 0.6227324288596917, 0.4090428063990235, 0.20203339856201763, -0.1268532492093506, -0.24498897984964926, -0.34240522912447924, -0.41329938001512057, -0.47454554376028824, -0.5624776609423913, -0.7106624653026689, -0.9330425016706583, -1.215500584387008, -1.5197744294054332, -1.7998610106952972, -2.014506986310325, -2.1355670618337355, -2.154261392864251, -2.081077136152666, -1.9381895587709002, -1.7506463627261375, -1.5564015657123726, -1.4027862541558336, -1.3262073647204824, -1.3398927700439904, -1.4222492594562508, -1.5161883356974974, -1.5680959404554675, -1.5625908906358932, -1.507986879125811, -1.4026218335859515, -1.2407021790292794, -1.0222137951734542, -0.751131139771175, -0.44173967592858565, -0.11156076928570755, 0.22396366950928276, 0.551623339966369, 0.8596166728308857, 1.1308845417161664, 1.3444095303250794, 1.489879774742453, 1.566574610922277, 1.577974249982508, 1.53304070736031, 1.4390995974727607, 1.300473893896537, 1.1234310767542675, 0.9153799604267288, 0.6873239493385501, 0.45460446297740165, 0.22587770622996492, -0.10885708128098437, -0.21189282653449631, -0.29919426112974123, -0.36267743418009885, -0.4111464475912724, -0.47208597151122855, -0.5772839387920475, -0.7496694844406983, -0.9910130162938432, -1.2791051259073776, -1.5787378969051904, -1.8500297382477997, -2.05746048570708, -2.180851402991313, -2.2191357776322547, -2.18580696278159, -2.1001863016868234, -1.9892713457549032, -1.883189491896076, -1.8027881783316408, -1.752641613427466, -1.721279825308266, -1.6774455881603114, -1.595208712734609, -1.4795687074536523, -1.3491698132698564, -1.2047922693165052, -1.034379806263575, -0.8274548021542087, -0.5773145441405273, -0.29145669363363763, 0.013612443699922771, 0.3217448218241529, 0.6193974521106395, 0.8947035569599756, 1.1354607511814003, 1.329808498957435, 1.4706263736156897, 1.553286872390097, 1.5772496323162588, 1.547350158544397, 1.4658371326152402, 1.3337970590989432, 1.1571446532500782, 0.9451768224898427, 0.7114459354036349, 0.4720507169041051, 0.23517486458479156, -0.09223483121772458, -0.18247750437565585, -0.2629211262525165, -0.322981314982973, -0.36395148474046407, -0.4051220141350384, -0.4738382106358736, -0.5963572485671915, -0.7867660466054273, -1.0378077384288762, -1.327369955864301, -1.62336258144586, -1.888212128047311, -2.0918803529732655, -2.2223250579389457, -2.2844127365845464, -2.289705288732265, -2.255745955957408, -2.201902158392876, -2.138458531957123, -2.0641549568288697, -1.9718598003943755, -1.8467290229729811, -1.678813303200242, -1.4799610169958377, -1.2737090797205854, -1.070343362335293, -0.8642142617524506, -0.6444604187951936, -0.402900854833902, -0.14267509228600328, 0.12494370738390854, 0.3893836997524978, 0.64217074461237, 0.8759768171059713, 1.0844413756465976, 1.2605729480891414, 1.3961851955274986, 1.4825989297470665, 1.5160612379959202, 1.4975809804572042, 1.425928258603944, 1.30118733417833, 1.1298824375557266, 0.9228628422645638, 0.6949762190808971, 0.461637982039308, 0.23015073088364688, -0.07752180778530936, -0.15695329017029852, -0.23325354348553168, -0.2944341155491393, -0.3344669583559029, -0.3641817235126848, -0.4059527004188185, -0.48570582795688344, -0.6245852896409454, -0.8269461814625987, -1.0816566623986759, -1.3670088175011168, -1.6520491682965854, -1.9041695375604015, -2.101436307702288, -2.239137900333125, -2.3206945686489395, -2.3544563960871807, -2.3520945930926764, -2.3187709602929676, -2.250778279901817, -2.142176061912694, -1.9856135172946616, -1.7778735661955993, -1.5312750766061198, -1.2714478762068, -1.0165313802674578, -0.7713233626849426, -0.531993443500024, -0.29365642233716643, -0.05725339946537988, 0.1719043255096742, 0.391442402866098, 0.6003781143851697, 0.7970409254544045, 0.9780867625595673, 1.1374533700071197, 1.2662491668871478, 1.3542238951481467, 1.3946044353074323, 1.3844132352558904, 1.320783336271209, 1.20493261998099, 1.044741133649296, 0.8522478568508765, 0.6420900774653417, 0.4271446656147565, 0.2131128876851958, -0.0671829050406794, -0.13762174880842773, -0.21005458244806652, -0.27473193312295874, -0.32070685951588196, -0.34967472064262567, -0.3770662378477945, -0.4255586378878923, -0.5188852326077295, -0.6695090003055999, -0.8749170522007259, -1.1226390296492677, -1.3917989748546473, -1.6559832761632798, -1.8891067759669036, -2.077152504518098, -2.216079855329806, -2.3059536407529246, -2.3508452929034394, -2.3522096307190186, -2.3066853876833995, -2.2094145162659484, -2.0566328039685864, -1.846918486257884, -1.5913681276550977, -1.3127820423369567, -1.0325817877959689, -0.7648184779250229, -0.5138481932287925, -0.27976346570891125, -0.06283772471404896, 0.13729339819909, 0.3236185724578833, 0.4998510369620811, 0.6672173922645893, 0.8238189759362649, 0.9654643526259635, 1.0847938625459128, 1.1712471417878765, 1.2155405939438775, 1.2116200231682346, 1.156426021381188, 1.0529940158019124, 0.9103426320791829, 0.7412483005187566, 0.5590207846606174, 0.3728386046138389, 0.186310094234003, -0.06419118815100455, -0.12853928606371728, -0.1957967273450474, -0.2629708700523488, -0.3184209712604408, -0.35524143127649743, -0.3807085164658563, -0.41218444150708544, -0.4714589188796244, -0.5750319252223569, -0.7268489464149748, -0.9221399772868974, -1.15010770536485, -1.3942900908960068, -1.6320483158558379, -1.8433320710804024, -2.0175384439567585, -2.1481813437890755, -2.2320545993124097, -2.2666519424020946, -2.2488040592132963, -2.1755215016640337, -2.045564313763454, -1.8585017943342326, -1.622992292233212, -1.3560120339930626, -1.0799200730972964, -0.8132777124503587, -0.5669781799580039, -0.3446557869875327, -0.14431630101589232, 0.037513242795302056, 0.2039553110996131, 0.35794222511016227, 0.5011708254165776, 0.6345618920682572, 0.7568142630232572, 0.8626830834681276, 0.9428789480544681, 0.9876652232543195, 0.9895134351387721, 0.9457867736379653, 0.8604271226313295, 0.7422789962288878, 0.603868077420758, 0.4564383841818994, 0.3055034168971221, 0.15297037956086554, -0.06846062810616416, -0.13108602820020446, -0.19259540216799348, -0.2583331187223633, -0.3214169443947396, -0.36981521082551944, -0.4018804893852553, -0.4289159870504006, -0.46869487457137826, -0.5372349654890848, -0.6421124342256782, -0.7836113725882364, -0.9589083152946737, -1.1619676601445477, -1.3782879396784606, -1.5873458001859269, -1.7732878051120458, -1.9249043500376541, -2.0335460532148444, -2.093493965102792, -2.100618476000928, -2.0529641695873, -1.9509483533845846, -1.7961356810528577, -1.5948491663772775, -1.3599941646181892, -1.1121189449460998, -0.8702892711506425, -0.6475074354865548, -0.44679925300023854, -0.26424361283250253, -0.0968759265318428, 0.055345750649160544, 0.1920717893744209, 0.31468937700521765, 0.4258489701497256, 0.526877083186676, 0.6157280568783234, 0.6860055761558634, 0.7289952496604368, 0.7368447600320518, 0.7076868455381147, 0.645650507165709, 0.5582562393900288, 0.4559497853426465, 0.3468611145577351, 0.23360603729783624, 0.11735912984045783, -0.0764855745854308, -0.1418857725658651, -0.19936151127546994, -0.25948729822387223, -0.3235135064292013, -0.38113706918967216, -0.42417670004156155, -0.4561115936992948, -0.4894005364228368, -0.5374082865021138, -0.6088014728517666, -0.707005101633663, -0.8331555363108161, -0.988579520841854, -1.1679655453192532, -1.3545948967268404, -1.5306314186128172, -1.6819527439775144, -1.7972502942297945, -1.8688013509749226, -1.892097707275962, -1.8649116823019214, -1.7888107964408064, -1.6669697921917142, -1.5050941769476018, -1.3137308385852073, -1.109545632732466, -0.9087293279739469, -0.7214111036247915, -0.5488229916779785, -0.3878048262497428, -0.23761805892306068, -0.10061411029694008, 0.01962972751678309, 0.12250622148438745, 0.21155539455230782, 0.29135507740748406, 0.36291564487539085, 0.42267674685656814, 0.46337897270597395, 0.47768105872573, 0.4648894013141604, 0.4290595351785681, 0.37557886917896877, 0.31126454381201374, 0.24061781990939385, 0.16435138024842466, 0.08334407367458108, -0.08487197134148547, -0.1563417371241633, -0.21297431398937108, -0.2655402028208873, -0.32330753299312176, -0.3829986133002652, -0.43557245017129237, -0.4778212079565376, -0.5143866893702937, -0.5541544107912387, -0.6058389148269032, -0.675217309438376, -0.765504158824181, -0.88029601367554, -1.0203987689370264, -1.1747816221699328, -1.3271670093208183, -1.4633488302825164, -1.5707853170492634, -1.6407550454820354, -1.6691661529058779, -1.654411778375531, -1.5985392885605372, -1.505935770964325, -1.3819008808226887, -1.235101882228747, -1.0779168238638301, -0.9218850001749962, -0.7729641532770791, -0.6313557497704746, -0.49594640631838083, -0.3671421209212011, -0.2486308174645061, -0.14700844386381742, -0.06437434411302564, 0.004048549423741131, 0.06492796727620102, 0.12126952131879473, 0.17206144843765378, 0.21193909760208776, 0.235065078371512, 0.24107601127916403, 0.23246444011799194, 0.21197521798137522, 0.18288335296960848, 0.14693008013321757, 0.10380738833501028, 0.053927894633230784, -0.0921329049444279, -0.1712490015450831, -0.23070859222283316, -0.277090397702021, -0.324221661539021, -0.3775944043788554, -0.4326807611534665, -0.4843667909881887, -0.5301332864467335, -0.5717330693745103, -0.6159025469731391, -0.6697290545683369, -0.7379878556967086, -0.824423828122845, -0.9312850164120254, -1.0529389843468906, -1.17725915484989, -1.2925081396647176, -1.3857279386269516, -1.4469858550578765, -1.4725506208909696, -1.462533267170287, -1.4194436967715927, -1.3487175171025407, -1.2550694054850478, -1.1454988100190624, -1.028721725042726, -0.9127064486960542, -0.799992045143042, -0.6900125408253859, -0.5823256752040767, -0.4776634583837224, -0.38127713941856867, -0.3006068786855628, -0.23777852676232927, -0.18738177702049078, -0.14181296323265385, -0.09703101231419595, -0.052301084738729985, -0.010179082305791927, 0.025478381803686726, 0.05266207013173684, 0.07078896594379812, 0.07985114563438674, 0.08039842732279805, 0.07279581566546876, 0.05629238371626541, 0.030929530473562696, -0.09822947022896533, -0.18473794380806852, -0.2500687500358799, -0.2951130470521729, -0.3320617119107919, -0.3725110876813336, -0.4200954291838236, -0.4732036603007206, -0.5268684943282185, -0.5766292554376088, -0.6241415202226319, -0.6746196519579936, -0.7324844426292038, -0.8014246237540209, -0.8834072027268793, -0.9761197391727963, -1.0730195100408288, -1.165989414127373, -1.2432843764426684, -1.2936692323751577, -1.3132312454923052, -1.3029767553603053, -1.26632877239839, -1.2093933033014757, -1.1374501726813788, -1.055533901169824, -0.9700414135619917, -0.886400144898103, -0.8050549188284704, -0.7243718411903921, -0.6436052697896137, -0.564793409561435, -0.4934834772990283, -0.435443683827131, -0.3916666260513632, -0.35570989769114636, -0.32018315370418576, -0.28184833914042295, -0.2390509888250298, -0.19142219168736052, -0.14170247589215357, -0.094100653910263, -0.051918332066764966, -0.017913511531682958, 0.006300505639173847, 0.02043209439624498, 0.02313993837381771, 0.01473156459167701, -0.10371843292567662, -0.1959999296696074, -0.26728363958837315, -0.3149605700270558, -0.3459278194981688, -0.3722637616801856, -0.4047577651999499, -0.4483030694885056, -0.5006195097209792, -0.5562111685847467, -0.6120050028062655, -0.6676898346233253, -0.7243135419384347, -0.7843670049769953, -0.8496779358125227, -0.9195938721389527, -0.9922661187180942, -1.0634634707608661, -1.1238401556146216, -1.162672630930289, -1.1754026950606136, -1.1626102218466707, -1.1281839963852585, -1.0792748776818242, -1.022226942596446, -0.9605989804814034, -0.8990130042913611, -0.8408381845786791, -0.7856193056294315, -0.7307033546065272, -0.6758554023668152, -0.6239622068980544, -0.578830748896745, -0.5433692661594215, -0.5159818245218734, -0.48983780761790385, -0.4596119315095659, -0.4231397520676042, -0.378040358113962, -0.3230252924880197, -0.2610784443110707, -0.19699302623224968, -0.13560201337184458, -0.08244693260187165, -0.040626998392256815, -0.011073523531920431, 0.0037469024701141593, 0.005096026603037013, -0.1075676920534544, -0.20257430423979544, -0.2758654078186644, -0.3245925269181256, -0.3523583756897912, -0.36854399695991963, -0.3861372637330806, -0.41472888221919796, -0.45648854251944165, -0.509188209734131, -0.5687292016481976, -0.6295574522622375, -0.6877977332690812, -0.7434607639259055, -0.7977167275704726, -0.8509777700808165, -0.9040483395807085, -0.9558161403333306, -0.9994361010664172, -1.0262957527452694, -1.0318096136414026, -1.0157957800943007, -0.9820782105261702, -0.9388965594934433, -0.8929707242422295, -0.8472627967415969, -0.8046599135323147, -0.7673829851020058, -0.7343494896824424, -0.7029558038321452, -0.6734425008575105, -0.6474966462887716, -0.626255950377664, -0.6094718566421077, -0.5935993686067629, -0.5734301383591283, -0.5458772871426099, -0.508901466943429, -0.4600774328248894, -0.3991904295332192, -0.32940533503130465, -0.2544327921752015, -0.1802730329861126, -0.1151294614205421, -0.0628957250367032, -0.024932802199809655, -0.004524521540269648, 0.0008001072847105936, -0.10599001017655275, -0.1980500577175008, -0.26698447037799566, -0.3113861992024307, -0.3350775625428965, -0.34537960195880524, -0.3537139676402354, -0.3703496259913204, -0.39993988432345867, -0.44347232695041694, -0.4981582056950935, -0.5566557003927045, -0.6119839125243302, -0.6616904995435439, -0.7057806891045232, -0.7452305823700707, -0.7823815525099057, -0.8178372986590742, -0.8466618725207089, -0.8622379756749916, -0.8610905813860363, -0.8429752801297341, -0.8117410716525807, -0.7753682822117104, -0.7399697074887654, -0.707906575655623, -0.6810227560002962, -0.6608747668629389, -0.6460971078998388, -0.6350292017217627, -0.6275128197189452, -0.6231097074708346, -0.6202906619691813, -0.6164356706552863, -0.6076493392636367, -0.5906090278034871, -0.564125081218247, -0.5270255648028325, -0.4775785234227454, -0.41627099343692303, -0.3452744698754367, -0.26704259656071094, -0.18869753587807697, -0.12030442181046555, -0.06610246859047457, -0.027125737919711585, -0.006262983049217299, -0.0003492452283138823, -0.09447857743727585, -0.17506011777600428, -0.23311687367056633, -0.26873844371313094, -0.28670551348333867, -0.29306617213324687, -0.2967679041388411, -0.3067637718983051, -0.327833608433876, -0.36150232120404807, -0.40563044419022404, -0.4537608296090468, -0.49919966550315015, -0.5384711434570882, -0.5706467582715836, -0.5969055262247539, -0.6205467631342971, -0.6428091446955878, -0.659872574750666, -0.6665680676949912, -0.6609096430479022, -0.6434714996101101, -0.6180042162333664, -0.590745080197934, -0.5661685269291062, -0.5458679514588353, -0.5314156353726069, -0.5236351831725785, -0.5213525750870354, -0.5238672665451517, -0.530727752380745, -0.5399365028645782, -0.5483778513215237, -0.5525201270049432, -0.5482344295606714, -0.5331114647354073, -0.5081403889505532, -0.47401421708921226, -0.42946815852581227, -0.3744922839418025, -0.3102811821563436, -0.23877300260201278, -0.16702903859251822, -0.10510881308647126, -0.05710857621158746, -0.02312829898727592, -0.004956445518651291, 7.288259615985393e-5, -0.07105235621764437, -0.13082832208692122, -0.17269112925485497, -0.19743104445966717, -0.209291531378948, -0.21253730900392112, -0.2135972082073573, -0.2197060982818436, -0.2347717408048235, -0.25914598668676153, -0.2903827348367224, -0.32376343729636736, -0.35483773211044417, -0.3808513735770388, -0.4006576384507056, -0.41543039727304737, -0.42838115677304783, -0.4407120819259999, -0.44947132365442566, -0.4509024520517794, -0.44413194759978597, -0.43049372946707787, -0.413013810541572, -0.39564101102923455, -0.38079836514633475, -0.36959587262898924, -0.3634318872389831, -0.3625171305289042, -0.3658952249962141, -0.37338129582532603, -0.38470187712131576, -0.39766489786493886, -0.40941683595218137, -0.4167993831331151, -0.4156368831361434, -0.40398485867291917, -0.3840975852419937, -0.3576661197621121, -0.32343689166413137, -0.28101833927685094, -0.2317024993629399, -0.1772526771397208, -0.12287346240693539, -0.07631237998125295, -0.04079905636984499, -0.015767285260712458, -0.0022258173669206203, 0.0011547714403939901, -0.037951471967316394, -0.06967627931050242, -0.09160709659736065, -0.10437356177350472, -0.11032055220774517, -0.11148564747237556, -0.11134596238693613, -0.11427964591576308, -0.1226463168496043, -0.13606112128574105, -0.15256283124054426, -0.16955882574133319, -0.18501490143420307, -0.19762613631500184, -0.20668863598023232, -0.21297070585630234, -0.21843055099997746, -0.22378533444139706, -0.22731257946748717, -0.22698739355605363, -0.2225519236521291, -0.21512464298702869, -0.20635587552832127, -0.19805147262921471, -0.19112852165980088, -0.18629243464605266, -0.1843793398287231, -0.18538122177819055, -0.1886407478427701, -0.19410262934769434, -0.2017117914299837, -0.2102091555376654, -0.21813519663572553, -0.2236388419153256, -0.22393244628329664, -0.21784066284305229, -0.20700360461923623, -0.19258967241858882, -0.17367817848828157, -0.15007465918756663, -0.12302021035465702, -0.0936781481512868, -0.06456248608490646, -0.03970759266349971, -0.0208506964502549, -0.007464442238529875, -0.00014161389158973508, 0.0013930476764658461, 5.5261602541510655, 0.047367791750624645, 0.08544607280267481, 0.11751647294944044, 0.14054085168615923, 0.15489690298954611, 0.16487957116133636, 0.17826529739833888, 0.19433080253372959, 0.21081655094036622, 0.2236822918072351, 0.23048879012851492, 0.2301333938923407, 0.23206148226458145, 0.24419817574771716, 0.2640884654405951, 0.28498973991446547, 0.296549567129654, 0.30148708703995836, 0.3028017224075431, 0.3010461606438139, 0.2955075213896987, 0.2809648943419486, 0.25774012975611865, 0.2293566718778449, 0.1991115113820876, 0.1660979941488264, 0.1249162138140006, 0.08092027385448546, 0.02794883506122277, -0.02765959127037319, -0.08241450363319594, -0.13692308295105915, -0.18211671673912264, -0.21682809637845063, -0.23268785896156485, -0.2343673944006283, -0.22683904185678358, -0.21310830874720496, -0.19614799712150915, -0.18102386506608603, -0.17423642862836633, -0.17684528205059286, -0.18618013882930817, -0.19429293547057783, -0.18854748719324965, -0.1647642200142935, -0.12394011951966195, -0.06682066304687494, 0.095050987444916, 0.17373790276161255, 0.23864363999877453, 0.28606418524782545, 0.31844156628123466, 0.340873597103774, 0.36374519242056036, 0.3914671294575676, 0.42090002893114087, 0.4412379679152373, 0.44890135070769654, 0.4489019603251674, 0.4571053895988182, 0.4816001034219493, 0.5140630541169131, 0.5472560101592842, 0.5703849783867072, 0.5828654023903496, 0.586544552967273, 0.5819441756365612, 0.5663848542636967, 0.5350712458425229, 0.48918223781456704, 0.4344158824495984, 0.3728432311704634, 0.3063438520494887, 0.22584862389056948, 0.13635773369702828, 0.034700065163745596, -0.06752254333792475, -0.1650632220894713, -0.2587070954337544, -0.33502671018757296, -0.3924108755903818, -0.41901924240780947, -0.4229120106675896, -0.4117773014875915, -0.3876201213091618, -0.35922853200103627, -0.33400887904746823, -0.32432606178640644, -0.329382432497961, -0.34134027052342425, -0.34919229261713924, -0.33669697418767186, -0.2895547943965154, -0.21470134213003253, -0.11567643139681641, 0.13493918675511424, 0.25183170638660674, 0.3473493335487015, 0.4198087660207144, 0.4727572740891326, 0.5118785615268452, 0.5448102386013586, 0.5797430859553766, 0.612759272933439, 0.6337096031200234, 0.6423928346963041, 0.6448242779106704, 0.6576394316344508, 0.6883487601028604, 0.7238362468646913, 0.7583648776534645, 0.7897061126916259, 0.8136927709206143, 0.8268985684164928, 0.8255383476425717, 0.7987216544547345, 0.749161940873383, 0.6806615814863789, 0.5992529902482246, 0.5041250509639161, 0.4026352279453095, 0.2839666588709371, 0.1537750282337281, 0.012788950479099052, -0.1267667143872052, -0.25388210254307103, -0.3660493267523953, -0.4540945081535071, -0.5161231934265074, -0.544292083504707, -0.5476583135146702, -0.5338127620934318, -0.5032415665102461, -0.4685899391498285, -0.43674336830588373, -0.4272866838254305, -0.4364938800420878, -0.4489749100596314, -0.4510098555851533, -0.42970040657409647, -0.36257964806989973, -0.26413351723624384, -0.14226015583295953, 0.15959083521395417, 0.30187916922410796, 0.4185740876406424, 0.5128650814540122, 0.5892454462223085, 0.6500500160425986, 0.69897204395704, 0.7407978944853806, 0.7710370864690143, 0.7879336517213772, 0.7976520307658997, 0.8043446289327331, 0.8211164732248688, 0.8533861529887329, 0.884988344551476, 0.9128287648836985, 0.9450332281550367, 0.976170985771238, 0.9946387629928148, 0.9954561166926945, 0.9594926437126668, 0.8952079498409219, 0.8074863432705445, 0.6991847756022118, 0.5727498461618447, 0.4400508574587691, 0.28644694274132015, 0.12060831607106594, -0.05155079487274001, -0.21855231192875063, -0.3623833314460703, -0.47710965807625894, -0.560561124662012, -0.6102498973155348, -0.6278813898096333, -0.6206313699780284, -0.5946035714334995, -0.5577582719490465, -0.5196828192463716, -0.48667163611603786, -0.4811437470465423, -0.49733759068709366, -0.5116101338846597, -0.5061458844543003, -0.47291315894765884, -0.3914697094253936, -0.2800872452911396, -0.14980964980901854, 0.1652749874085072, 0.3137110399668429, 0.43732714618556423, 0.5447551338904393, 0.6439527692367992, 0.7318510853452004, 0.8010399892546074, 0.8501866143742065, 0.8809020758795744, 0.8991657603007677, 0.9137275905467342, 0.9278182193881169, 0.946584498522865, 0.9717319368057356, 0.9905556142128827, 1.0057061584901057, 1.0314227450082858, 1.0630804466379422, 1.0807392952616868, 1.0769472822393173, 1.0296650872176039, 0.9475607018233726, 0.8388827715443129, 0.7074141111012296, 0.556402485803139, 0.39853295962441665, 0.21873848855563696, 0.024279946579141228, -0.1722300278309666, -0.3542835491299042, -0.5032632109571529, -0.6112993323916139, -0.680368968835457, -0.7066686454597685, -0.7001815228339222, -0.6704056430091229, -0.6219021874732573, -0.5732307217276775, -0.5309450160251704, -0.5010919313743402, -0.49995818459092795, -0.5201387812074743, -0.534107892173516, -0.5213073034258223, -0.47640434159329703, -0.3886837233517783, -0.27346726938846083, -0.14332647560239772, 0.15364104062766534, 0.2904334663042697, 0.4092741884176734, 0.52698278327689, 0.6483102852115032, 0.7624729066268328, 0.8491184079032448, 0.9055110747125884, 0.9401427536289702, 0.9646329194272625, 0.9891319821634812, 1.0153367579278765, 1.034591998021156, 1.0442981301064318, 1.0423912225580392, 1.0369932718142376, 1.0458660948695961, 1.066198049781203, 1.0725064524661507, 1.0535519272145806, 0.9910990255287062, 0.8931293157353684, 0.7680981006237833, 0.6203299042927489, 0.4492556451129088, 0.2699239929006282, 0.07442261933135369, -0.13563453908242384, -0.343389941450413, -0.5268437694463747, -0.6727907513391157, -0.7709584553490109, -0.8232380620812362, -0.8229404542426313, -0.7835436810287483, -0.7197343954742734, -0.6412353379810382, -0.5721269046672163, -0.5214999053767457, -0.4956776742969352, -0.49997524173643565, -0.5212857260391087, -0.5320131965499157, -0.5113473223582428, -0.4564340148237122, -0.3658561122429588, -0.25144941839374446, -0.12674906787810636, 0.12880391757765028, 0.24705003701983141, 0.35689529312820745, 0.47971646219197894, 0.6163727001001496, 0.7502730052594605, 0.8509492545090728, 0.9177912223817161, 0.9598499783107963, 0.9932711704524485, 1.0284839584148584, 1.063198454052275, 1.0796446807934525, 1.0735843841518777, 1.0499708981449956, 1.019397408817023, 1.0021896571386584, 0.9977060730549472, 0.9779798149548462, 0.9329389632496955, 0.8501499159318913, 0.7387823979463692, 0.6015406588847959, 0.44004948415943224, 0.25071183295735805, 0.04857880832953902, -0.15949763559369304, -0.3719086840575867, -0.5722986776456965, -0.7416358178805947, -0.8700539797296907, -0.9482262241625138, -0.9758341364922801, -0.9470721694323132, -0.8758871142404023, -0.7764416258818273, -0.6667553246311115, -0.5728465052648308, -0.5101147315061443, -0.48462060493855924, -0.49148110221887353, -0.5078367994433733, -0.5085967620980372, -0.4785191320557934, -0.41751753554992793, -0.32809154660168743, -0.22225089771323328, -0.10885020367220964, 0.09412626670950829, 0.19060357170471803, 0.28980761153307544, 0.41484435557059524, 0.5623471057189678, 0.708566588907289, 0.8167455894506207, 0.8933445098893392, 0.9447029412446001, 0.988473392228032, 1.0337705976548779, 1.0730160017561081, 1.0846556560061382, 1.0648810374170559, 1.0214307954775588, 0.9685736400475309, 0.921740513310636, 0.8792313619369663, 0.8177121758733334, 0.7392191037297665, 0.6352112866659019, 0.5122133795955364, 0.3625859970993863, 0.18368178495474585, -0.025706111958391207, -0.24770679560243378, -0.463598928786382, -0.6687980410490496, -0.8494371572059517, -0.9928306577908369, -1.0877263026630115, -1.1315710738929525, -1.1236196278710082, -1.0634116383898862, -0.9612127474196962, -0.8284138568222014, -0.6900635658807892, -0.574395433778138, -0.5000073161644627, -0.4696920085288885, -0.47268329909649126, -0.4789605523438417, -0.46788523627924566, -0.43041369385704725, -0.3653862981570702, -0.27739363925010013, -0.18182509339257438, -0.08724376187223411, 0.055375041586910256, 0.12226563081329078, 0.20744229093053337, 0.33418697808176406, 0.4908151046465711, 0.6446423820047552, 0.7579532205691445, 0.8424655383361105, 0.902411188841071, 0.953971693348368, 1.0036548482802383, 1.0410237139312506, 1.0440494143086032, 1.01630855025352, 0.9630740337734233, 0.8962588943754393, 0.8204519492801482, 0.7354545263554366, 0.6278307229716354, 0.5125073067674843, 0.3877907948945643, 0.25141398598373227, 0.08584020390864519, -0.11534332730891417, -0.34714124066055085, -0.5839743240134075, -0.8043786686933345, -0.9995805628384026, -1.1534106593778326, -1.2584435397380782, -1.3069722355597135, -1.3032208348318737, -1.2494583898452976, -1.1512522635661593, -1.0166704143264906, -0.8585241493156378, -0.7010173058695929, -0.5695158400076987, -0.482972491301144, -0.44103241925297537, -0.42915650809637235, -0.42172392925892155, -0.40196937225923546, -0.36142237407566213, -0.29733318245030166, -0.2165001338235831, -0.13323787269920892, -0.06184553747131714, 0.018035874620239964, 0.05298333959221811, 0.12403180244421412, 0.24728120033889203, 0.40591189607770717, 0.5653906957617595, 0.6881811229815455, 0.7789350064623329, 0.8430918039559295, 0.8970259938363283, 0.942831641764146, 0.9724381939315072, 0.9660683138955907, 0.937876869051629, 0.8860245787578628, 0.8123705829574799, 0.7128152396955464, 0.5915359964105391, 0.4452013418506707, 0.2950120290607255, 0.14808458740972918, -0.009791889275919508, -0.1980854897403521, -0.42400197650080085, -0.6751347260584333, -0.9211141865673497, -1.1425638891361114, -1.3241358056013066, -1.4465111453923725, -1.5024096146927706, -1.4933983229394394, -1.4302495654484337, -1.3236351082633184, -1.1826449425660073, -1.0157525751970176, -0.8365916467899356, -0.6628886048721071, -0.5165860669388354, -0.41777430998436565, -0.36399187910611386, -0.3385166483590461, -0.32465167095933983, -0.3079035795470122, -0.2778204816608332, -0.2262042179703915, -0.15933559879927123, -0.08906888384282018, -0.036481997065948006, -0.01231772622157964, -0.002529917202939276, 0.055209392180732585, 0.16793004475371012, 0.3189718161402849, 0.47965531121232197, 0.6098830231580585, 0.7026352093902061, 0.766308253435052, 0.8173479932089489, 0.8515709743799998, 0.8723262957323938, 0.8669125419473984, 0.8479686491695907, 0.8056263787322279, 0.7318009744160606, 0.6187314010559551, 0.4731476368659214, 0.2989341887569332, 0.11975424596522931, -0.0532617043584079, -0.23981380081767922, -0.453332884187915, -0.6996276494423647, -0.9631125826370659, -1.212282146572071, -1.4262413243781549, -1.583814597069304, -1.67049396340163, -1.6765199555295773, -1.607345006677459, -1.479937241211999, -1.3172880695456766, -1.1315429990866943, -0.936386416160398, -0.7424620191086378, -0.5607212033430631, -0.4066437989301752, -0.2977944303281449, -0.2324965458613548, -0.19886339064963438, -0.18655293964796066, -0.18283961496203857, -0.17521191256924945, -0.14328061304260847, -0.09275113045106373, -0.03964566337070431, -0.007603050531553751, -0.030682028616474642, -0.03673496941575852, 0.01022285603222707, 0.11254530493906491, 0.25235830981912744, 0.4069363218777887, 0.5373480355334527, 0.6313838025874885, 0.693147792192772, 0.7355766567886948, 0.7537797632592886, 0.7649135000028894, 0.766012157354184, 0.7574995058402678, 0.7225845440019136, 0.650757652001611, 0.5351493142274897, 0.3839373621825764, 0.19875491870499762, 0.0011310577251356943, -0.1973785528720183, -0.4105524581670198, -0.6458520517375623, -0.9047213317446319, -1.1685194506278451, -1.40688865831804, -1.5986372638714998, -1.7236205053641127, -1.7716416166118396, -1.7340440721007888, -1.6135491468053926, -1.428526707001289, -1.2106468918692244, -0.9819199821039262, -0.7651846798502346, -0.5657688003983605, -0.38832053342508116, -0.23807953663282233, -0.1267775309990522, -0.05827700937917978, -0.02801399019440153, -0.024958672394927345, -0.03656470985860989, -0.0537906121661246, -0.045416740654651656, -0.015608555871188964, 0.01485549622553169, 0.02303269708973007, -0.03874012442999659, -0.050159873620280515, -0.007690068878948485, 0.08641709485369659, 0.21337114119053877, 0.35746931158380746, 0.48631701583571496, 0.5815928264250224, 0.6380387231897693, 0.6680493444527745, 0.6764237805089223, 0.6846168954860875, 0.6908725132065702, 0.6854779126763821, 0.6502631746309369, 0.577746336990034, 0.4621983144822468, 0.3129394530481252, 0.12708730388324702, -0.07854933294342102, -0.29325671927171887, -0.521791773614181, -0.7662142380968706, -1.0218021458597133, -1.268631214221897, -1.4806723336577987, -1.6380471681351205, -1.7260746189856209, -1.7322566133653692, -1.6521886533999324, -1.4893614544229943, -1.2634696488852706, -1.0074047915607958, -0.753266500350333, -0.5256288014224608, -0.3310354517702326, -0.16832525872507145, -0.03318255923394563, 0.07006880575728369, 0.13159196740278384, 0.15031070780309044, 0.1388361462236717, 0.11278127077839328, 0.07838662230245422, 0.06472650236675408, 0.07043839066718473, 0.07611033625171985, 0.0550149518859174, -0.03712739969359494, -0.045204711340722924, -0.0020730571678541088, 0.08836014581784364, 0.20944034268671488, 0.3462682381366369, 0.4748448719525073, 0.571674934210147, 0.624209081147618, 0.6448853537134325, 0.6502943382838101, 0.6605987476215988, 0.6673050889749942, 0.6570435749352634, 0.6138957245720125, 0.5339557395394844, 0.41587726276208686, 0.26587625274199483, 0.08046183540344311, -0.13020645465376765, -0.35378997347799834, -0.5853114459485519, -0.8187768927331692, -1.0481694448302945, -1.258479406435871, -1.43128242808901, -1.5466891717050122, -1.5951404841457146, -1.5651574571879294, -1.4518584606279468, -1.2583625902599869, -1.008154166271318, -0.7361827072807643, -0.47776242274683045, -0.2529894923859628, -0.073434805441341, 0.0691511777104648, 0.18045143283420417, 0.26063184919185955, 0.30174247015066286, 0.30509844217462573, 0.28029722215231984, 0.24299148687525654, 0.1998228677133498, 0.16793619608084817, 0.15081240257894474, 0.13326231497547567, 0.0835897794006752, -0.025294987107138085, -0.021054996292198775, 0.02930550697867432, 0.12142477497856137, 0.24257952951471096, 0.3752030133821553, 0.5052949325560531, 0.6086998658798068, 0.6690343298486828, 0.6942015342073977, 0.7025637760832782, 0.7118604598640292, 0.711271927360977, 0.6901697036761317, 0.6330554664750397, 0.5368086757202897, 0.40809338131327033, 0.24872636211865953, 0.05813773338836601, -0.1582093130427664, -0.38338698723677195, -0.6049377476372193, -0.8108460584695144, -0.999111181342103, -1.1578939510272719, -1.2783279433510877, -1.3467912543319696, -1.3538627388173385, -1.2924955919080303, -1.157943849364205, -0.9539170267994852, -0.7016430816970545, -0.4362862167963288, -0.1936700333685986, 0.007446911932541268, 0.15790102541509876, 0.27406001983456474, 0.35666330283542347, 0.4050653874971247, 0.42000835112797397, 0.41090386526534306, 0.3804651320636162, 0.33605090903630286, 0.28679657159272665, 0.24026222903279687, 0.20405352335009921, 0.1640851227244468, 0.09504027855787589, -0.004553971728095692, 0.020589245730369764, 0.08742207682882847, 0.18929398658769703, 0.3142646508995481, 0.44853559267766996, 0.5820353897418692, 0.6950544412933469, 0.7711589851666032, 0.8089836603936145, 0.8254763738275412, 0.8340650206112777, 0.8245104076175863, 0.7877525970211511, 0.7105072859327212, 0.5912971649724237, 0.4447738932369829, 0.26949770514212384, 0.06634797100429542, -0.15775974393563685, -0.38083700157099665, -0.5839012737941166, -0.7542911269837462, -0.8958043759435274, -1.0023761951839927, -1.0692795928211296, -1.088619739081333, -1.0530139354562686, -0.9625876016180074, -0.8164127905575063, -0.6184774507107131, -0.38256294095813004, -0.14138957186417725, 0.0696599252026377, 0.23324077020275713, 0.34597146370460835, 0.42614731096282826, 0.4731123716103548, 0.48541961106169296, 0.4694534924724129, 0.44154416570797167, 0.40469606077801085, 0.3547228701355694, 0.3000633252591164, 0.24434094897356973, 0.19767982996552227, 0.14718384024193276, 0.07994716145599884, 0.024056500784839643, 0.07691869883235926, 0.1672612328388156, 0.2867837136635554, 0.4191050332573703, 0.5593611993053276, 0.6986701023284031, 0.8231678179615018, 0.9174138661920999, 0.9711769000368218, 1.0004836529233871, 1.011982960152405, 0.9947325606669456, 0.9351553869855633, 0.8305148161424175, 0.6837060346307087, 0.5138817675205853, 0.31996317898349746, 0.10122612603497924, -0.1299483231094366, -0.3465032131315751, -0.5264576514017929, -0.6617587593805125, -0.7574920052211686, -0.816071161415853, -0.8325239371105443, -0.8007956269774802, -0.7260949413567344, -0.6137416589941552, -0.46355336041742107, -0.2805811375627171, -0.07677771240265473, 0.1229834707686138, 0.2892108379040822, 0.40660243800602225, 0.47522124754231376, 0.512574086326615, 0.5188814637443425, 0.49337832366412476, 0.44199577830512804, 0.38396752719254407, 0.3308538713654743, 0.2750394261259571, 0.21722725949022265, 0.15723874051317502, 0.11060530246891735, 0.07215984057074822, 0.03658700333864874, 0.05981826087054066, 0.14638210124082676, 0.2644999369043999, 0.40380263886796686, 0.5486690059266011, 0.7014834232768907, 0.8525366094504542, 0.989707085760694, 1.100912698443214, 1.1719168039961452, 1.2147433770426361, 1.2268935260596978, 1.1968038258894822, 1.108360042333312, 0.9705973604692385, 0.7904211648661325, 0.5905953443317823, 0.3752810990579086, 0.14323287080182565, -0.09048348049271622, -0.2948419267491915, -0.44852441569817864, -0.5480054662840163, -0.6020043359025783, -0.6165030796388667, -0.5844948562399211, -0.5049881496827973, -0.3976564448363887, -0.27029142291382857, -0.12148440507384309, 0.04168307091252923, 0.2058024647994756, 0.35583585187776895, 0.4677627660480422, 0.5313418189830315, 0.5504780475842274, 0.5424150756324294, 0.5035650957163699, 0.435449453758325, 0.34527790147159476, 0.25246172006423107, 0.17453469374569486, 0.10679878989135702, 0.04618246867171159, -0.00838956101315896, -0.03993322390640222, -0.044714457765848516, -0.02599314824275477, 0.08785471132367659, 0.20363262784307914, 0.3494625773174208, 0.5140704084379417, 0.6857013685744963, 0.8630050801641795, 1.0324519105712167, 1.1793686501873564, 1.2992902484828879, 1.383570714928947, 1.4369657737468327, 1.4476309091152006, 1.4038776780910238, 1.2866732944751131, 1.109483747846977, 0.8885796650000591, 0.6531626658329368, 0.4135194752309647, 0.17364846091129493, -0.051966247733642064, -0.235502981286509, -0.36272293076495904, -0.4248543806858992, -0.43460920701778344, -0.4045017975749699, -0.3290962412400327, -0.212210586480445, -0.07759032305425753, 0.060970984566674956, 0.20273976895331686, 0.33950217191189597, 0.4618307868153312, 0.5610756966199432, 0.6151606803082207, 0.6231907216169733, 0.5929251924693395, 0.5392258584954978, 0.4552217230433745, 0.3435370897217165, 0.21514524946639607, 0.08934365644390709, -0.016326044069055794, -0.10251649083879566, -0.17131225026809804, -0.216761775060635, -0.221119249710633, -0.1790130619780615, -0.09553010740118335, 0.11046209039549339, 0.25028400172577314, 0.42090745512759753, 0.6119352133990562, 0.8148978898943595, 1.0192650225503552, 1.2082965501026175, 1.3635207331604122, 1.486524307012549, 1.5763682586468861, 1.6320685274731495, 1.6364162243620155, 1.5798194679525264, 1.440423449786838, 1.228355423840176, 0.9707869055550841, 0.7046122145816187, 0.44453689090297227, 0.2021687912864298, -0.008079486448208136, -0.16402072386126879, -0.2605187464273912, -0.28444916825516703, -0.25005482189141964, -0.17621037462595068, -0.06697669751401375, 0.07172459126208149, 0.2204396820546456, 0.3609638602017775, 0.49226650738422634, 0.6051799550253236, 0.6925570263512455, 0.7447421470455117, 0.7419742374745922, 0.6937816952393261, 0.6147718443283492, 0.5156550141296805, 0.3918663593748037, 0.2442093353759338, 0.08277597584615114, -0.0716935433336437, -0.2043666484891755, -0.3091821843168853, -0.3865224108746784, -0.4232058488048183, -0.3973075634755216, -0.30686476796541784, -0.1620936633601367, 0.1323439108698113, 0.29173243332642407, 0.48290709626228495, 0.6985495992719502, 0.9272182837034186, 1.151140136517712, 1.356341821334183, 1.522039189196578, 1.6465038005172319, 1.730581107685951, 1.7766301566159088, 1.7708483811685964, 1.7031177266558508, 1.5472580356659011, 1.313348632202148, 1.0325939123191914, 0.7478531548690409, 0.483382080201588, 0.2526715750868865, 0.06316101820841914, -0.06736342932141805, -0.13040028114647076, -0.11551681551723578, -0.042459473645343575, 0.06461276989389653, 0.19187424577567916, 0.33428341158048624, 0.4790703420044476, 0.6097602926275395, 0.7270721895741945, 0.8232766434798687, 0.8885158801348368, 0.9058542424180381, 0.8563161169847773, 0.7581912440632389, 0.6351315610913785, 0.49514162146443863, 0.3357237819552195, 0.15586714936331464, -0.035682618356194074, -0.2160471864697252, -0.3724212559863471, -0.4932159216756074, -0.5751178346038747, -0.5987268641445389, -0.542009953498794, -0.4073689205342713, -0.21546943167670712, 0.15707111302136492, 0.33412710095520104, 0.5414961426335881, 0.7751985156384829, 1.017534510367502, 1.2480750726385605, 1.4584738009449922, 1.6312079055018431, 1.7557950454501694, 1.8290908879248047, 1.8601986520698406, 1.8431015748276727, 1.7663832997541629, 1.601748418862807, 1.3633805396188337, 1.0808960396757912, 0.800982249449246, 0.5535048835386314, 0.3473543126652521, 0.1838398418516463, 0.07608775869918326, 0.03998945468282868, 0.08127582784749798, 0.17608982488417008, 0.2969945669869349, 0.42468151574378404, 0.5538969554351832, 0.680915593494539, 0.7979626943551191, 0.9044910386650971, 0.9932759076809918, 1.048740287417887, 1.0466531010137812, 0.9652273550088896, 0.8260563430214086, 0.6597707004303978, 0.47806551986791496, 0.2825037623481919, 0.07419307447584197, -0.1403201069593761, -0.3390320594775737, -0.5080916876207123, -0.6358325373416014, -0.7160497576804999, -0.7240114543019264, -0.6445690679314771, -0.4788051240663911, -0.2553378751097966, 0.18182153201943632, 0.3777916078880683, 0.6001627663019503, 0.8389705283519011, 1.0761076284717037, 1.2987530735782946, 1.5050042362722684, 1.6785736591598337, 1.8013717953407413, 1.8648981026922178, 1.8789732130606231, 1.8460430563624892, 1.7589535609616922, 1.5966330034787883, 1.3746851303982854, 1.1189615112800204, 0.8723285041313241, 0.6627585548900583, 0.4960876246920122, 0.365491872208755, 0.2829348784803473, 0.2646669257504182, 0.3117681074659126, 0.40209598359006665, 0.5119937006490145, 0.619919898232925, 0.7234695053178464, 0.8258907745319803, 0.9261995053861818, 1.0249214122148929, 1.117040590772906, 1.177519429584973, 1.1708682330457587, 1.0724360003428608, 0.9032676193940004, 0.6983119389378522, 0.47805823373645606, 0.2468179102903589, 0.00839064788368874, -0.22898992522116804, -0.44340292912733237, -0.6164882990433371, -0.7410781875788645, -0.8121646572341942, -0.8005641828486605, -0.7013560194459284, -0.515604464801703, -0.27516675843720634, 0.1972362180054739, 0.40581531810065435, 0.6356421263196163, 0.8698171482311782, 1.0944911212531847, 1.303471759946235, 1.4982480483903056, 1.6624205850042486, 1.7779555252469568, 1.832780574774014, 1.8311437520663634, 1.7823408465418729, 1.6861119493669126, 1.536635020940506, 1.3486424903588088, 1.1434674743019433, 0.9535719357297167, 0.8027044485275914, 0.6932019166060523, 0.6026735492108277, 0.5438291310901133, 0.5307333737511967, 0.5633406365952273, 0.6270621277080666, 0.7075519562167837, 0.7863858676379308, 0.8636675055215242, 0.9407906447723399, 1.019623469856982, 1.1092980102480312, 1.2081854686924691, 1.2790157528897883, 1.2739719028808154, 1.1697933301194867, 0.9831805916295476, 0.7485982363434945, 0.4935730185347082, 0.22844110409222632, -0.04020296588642679, -0.2981308338332932, -0.5229493431274601, -0.6933740692117534, -0.8067731288150298, -0.8626898344490277, -0.8309317032095084, -0.7122767439680082, -0.5147377988450887, -0.2709780280263805, 0.19682567371139018, 0.407713169181388, 0.6327332964640834, 0.8538273608978156, 1.0601840441291348, 1.2488665952952995, 1.4242151252070554, 1.5710271190025509, 1.6742351240092344, 1.7200670251330497, 1.7069205253813917, 1.6469684510126823, 1.545518837073388, 1.4141461704660139, 1.2703870973475817, 1.1311511599887338, 1.0163469923500899, 0.9439258795573758, 0.9053942101372177, 0.8629598994981313, 0.8217931554645876, 0.8005455910979802, 0.8071854363698927, 0.8402201100795255, 0.8886010606981712, 0.9387893029300775, 0.991231712866265, 1.0447283320344847, 1.1014919908987502, 1.176006083737476, 1.2746686481419576, 1.353573459658591, 1.3526836208043682, 1.2507719485649615, 1.05728038407589, 0.8051138476262716, 0.5239360893108022, 0.23184921292419722, -0.06008840855428662, -0.3317794467364974, -0.5623513819913252, -0.7300404080477545, -0.8302569633585244, -0.8682199024575936, -0.8225493315017257, -0.6925901690104038, -0.4923228258663611, -0.25443805227463534, 0.17628962357570208, 0.37276810143565253, 0.5819575304139287, 0.78807078084093, 0.9766507236890037, 1.1404693922295648, 1.2843776676399652, 1.4015036621461114, 1.483136634210065, 1.5152509030456904, 1.491699506434832, 1.4235172788698351, 1.325873302498191, 1.2201453427379947, 1.1234433511570385, 1.0534455376714902, 1.0202824278396083, 1.0314069156651702, 1.0668589996213393, 1.081153212241913, 1.0607331356412797, 1.0341886073400473, 1.021108579235887, 1.0321715878242967, 1.057317727009447, 1.086516386378412, 1.1193949885674974, 1.1551371472922936, 1.192967540446801, 1.2458630119267466, 1.3337503593304667, 1.414127771800926, 1.417841816750596, 1.3205331752149263, 1.1255827195521368, 0.8622136031942897, 0.5607918441903206, 0.2469914647842444, -0.061486296300111175, -0.33839165614817485, -0.5671499169816436, -0.7333659136827246, -0.8250290178486485, -0.8447567785244784, -0.7829491945182225, -0.6465695672411929, -0.4539912606750856, -0.2327878037188901, 0.145531883955243, 0.3159535393931224, 0.5021561366630606, 0.6870722981787142, 0.8520920964772577, 0.9857560264492428, 1.0899139510546492, 1.1664122865801172, 1.2138981014064585, 1.2246615569254429, 1.1916553749158392, 1.121730159568028, 1.0388503757359433, 0.9620578123991552, 0.907712637605443, 0.900319931818431, 0.9399771192585639, 1.019292608294586, 1.1157849626918297, 1.1855303932998644, 1.1967216953493596, 1.183253960658514, 1.1732514140648402, 1.1818418242472672, 1.2023914066588257, 1.2271744855047941, 1.2527508418154816, 1.27985886175271, 1.3071343289247364, 1.3443766520470493, 1.4154235081703215, 1.4827530613843896, 1.4845882980336362, 1.3932870393819137, 1.2024890705581677, 0.9333199968362146, 0.6176220399458505, 0.2870413410548731, -0.033892579018304995, -0.313599934574621, -0.537935635576753, -0.7023590167077461, -0.7895405799263276, -0.7999955049850647, -0.7298576606857012, -0.5929608625658005, -0.41054711314752623, -0.208085752900938, 0.11695063293266694, 0.25390030745102643, 0.40721097328962885, 0.5604194936959487, 0.6914730271028449, 0.7866431615804407, 0.8447308238173076, 0.8731246757447221, 0.8795679859177697, 0.8647974491419459, 0.8239886009478146, 0.7627802667065955, 0.7043285578797684, 0.6616935873572487, 0.6461356628533954, 0.6841459444724031, 0.7736344717026419, 0.8957879662559382, 1.02997747115013, 1.141479323215209, 1.1959902838099221, 1.219826328735317, 1.2444017947243642, 1.279244071724568, 1.320663654685299, 1.361367010686283, 1.3965561062637817, 1.42743212777109, 1.4563061718107821, 1.494062586974992, 1.5528090821377483, 1.5986949528691534, 1.5864877699420579, 1.4905631551217533, 1.2983057218447842, 1.0263464386489818, 0.7020834933553013, 0.3603940416322589, 0.03434285887937208, -0.2425164421527456, -0.4595450949742636, -0.6217551353530676, -0.7093332899940118, -0.7195207507748315, -0.6548082343993856, -0.5291743474905327, -0.36371481586149373, -0.18299563558535312, 0.08955616328750923, 0.19055317957680654, 0.30472740938348697, 0.418660140568665, 0.5086068992015601, 0.5590532712097466, 0.5676857010277861, 0.5444014625844714, 0.5075740348121713, 0.4682859480979558, 0.4239211165727098, 0.37837634169492024, 0.34485213265339953, 0.33766997549845484, 0.36284740446048525, 0.43410145112505405, 0.5483103292018, 0.6867487131776387, 0.8359731052734227, 0.9755193060784861, 1.0802811133363295, 1.1594405980651628, 1.2423245949820443, 1.3270591534951524, 1.4095433088965952, 1.480526816875761, 1.538694833017479, 1.588844558472841, 1.6348667624713071, 1.6846713899882164, 1.7357101159101225, 1.7614558645792777, 1.7301657400729449, 1.6212713971428645, 1.422254000530152, 1.147650577596024, 0.8197655083910411, 0.47557617292502646, 0.15258725164038164, -0.11723570789362503, -0.32509502613439273, -0.48204394559091185, -0.5745068758313204, -0.5951413557707, -0.5494374379098592, -0.44512380509989685, -0.30592823536552494, -0.1547465425643167, 0.06311869704140011, 0.129591562772735, 0.2027613126479507, 0.27348526404400814, 0.3183710632787892, 0.3235059564462035, 0.28701091830624226, 0.22094563353601043, 0.14644507621490602, 0.08470233772085584, 0.03671580835942832, 0.003641302627799731, -0.0075892801455074805, 0.017145161469561705, 0.07871335860449744, 0.17545304659187871, 0.30070181265588813, 0.44354568893246565, 0.5999333242074067, 0.7586767364088639, 0.9063005870833284, 1.0468182435762559, 1.1982696177857846, 1.3443575031225667, 1.476343925367306, 1.5834381908785278, 1.668200055981222, 1.7413052831811366, 1.809835954010892, 1.8768018198716407, 1.9274877501870726, 1.9419704326402711, 1.8955019443175463, 1.7737087578176058, 1.5706355495604287, 1.2971455246844625, 0.974940914386742, 0.6390594350104252, 0.32745448796083837, 0.06936412947081143, -0.1288723953398135, -0.28215874542997704, -0.3866545196166185, -0.4291887037938378, -0.4145706959080228, -0.3444645681846359, -0.24174934518668942, -0.1252321173379945, 0.036107469733223214, 0.0699461609653685, 0.10493905889613869, 0.13687674836740343, 0.14300741577250795, 0.11261694156311852, 0.04097380290323795, -0.05808280079224662, -0.16487574326158666, -0.2498746876338761, -0.3074369994609883, -0.3377857872172318, -0.33120038449717215, -0.27944795814519613, -0.19053356667056673, -0.07356891315114181, 0.06077808087965531, 0.20562115510046017, 0.36528417890385995, 0.5352678490043347, 0.7129266549443415, 0.9073585517036957, 1.1213156581879056, 1.3293961376977048, 1.5141056558017065, 1.6605572669385997, 1.7723584459732624, 1.866717341124187, 1.9548302387589083, 2.037631434976055, 2.0919050791467786, 2.1023021004828077, 2.049110790107295, 1.9218010190702493, 1.7241584656749522, 1.4629626467494998, 1.1614489370910661, 0.8482448753923788, 0.5583145559976751, 0.31573194434631074, 0.12012789604951327, -0.03860824824400473, -0.16117795963156886, -0.23510788212360162, -0.2586869627982752, -0.23359218867821735, -0.1754128812515887, -0.09562594216955322, 0.011081560678062513, 0.017036420530530685, 0.02081276842963794, 0.02199278715229976, -0.0005185440248998937, -0.05354592935835877, -0.1490881234832822, -0.2757650526302938, -0.4129067500696062, -0.5242874879078179, -0.5972916199810935, -0.6294160755737388, -0.611138837812885, -0.5411077569756648, -0.4350903012950979, -0.3058558727787122, -0.16143029757272626, -0.008870997541925038, 0.15555532220703955, 0.33242594654558955, 0.5300118606818786, 0.763249666338793, 1.0266091058784885, 1.2874148742779972, 1.5201458660897276, 1.7065248005876508, 1.8468850117169338, 1.9609388707094546, 2.0623339466195674, 2.152898003984633, 2.2114839293602744, 2.2228742008654883, 2.1701782408950834, 2.045667225594021, 1.86142733706922, 1.623448080003371, 1.3521836206586304, 1.0722352735453817, 0.8098141874756339, 0.5811111561188325, 0.38357102825155315, 0.2146435052340916, 0.07083831378463873, -0.040736791444129894, -0.10808673256271936, -0.12986824535942548, -0.1149164533957625, -0.06915538319132856, -0.011558997632885159, -0.029986654699428485, -0.049896643885376145, -0.06681417587698145, -0.10282802529203162, -0.16651572107231977, -0.2782753573490287, -0.43070411077234094, -0.5974597452070256, -0.7368717821108722, -0.8282668075594427, -0.8629043607440492, -0.8375553099120273, -0.7574206962631048, -0.6395073775857155, -0.5000983793678841, -0.34480628531454854, -0.1825978809347025, -0.012491665542834963, 0.16845096890253639, 0.3753226478827628, 0.6265494975526646, 0.9204803123517435, 1.2232464653201065, 1.4994170689637336, 1.7225250082228105, 1.8894204159356176, 2.016132033915316, 2.119077864571967, 2.2042471200569524, 2.2644475558651602, 2.28126008180116, 2.2363578811475704, 2.1262169021441446, 1.9652503769393703, 1.760402996645559, 1.5231629745857422, 1.277016887782924, 1.0391650622607, 0.8204875736134405, 0.6208107955669693, 0.4400533033960377, 0.2747356284889264, 0.13320386362273176, 0.027921747114206478, -0.03238129764778501, -0.05334873471828675, -0.03896372325360012, -0.031940383270564136, -0.0679293888775512, -0.09840335808864324, -0.12309188412723489, -0.1655595075668707, -0.23829760344488032, -0.36487375425006097, -0.5398958205218186, -0.7305257758292498, -0.8922724517989029, -0.9999069072416281, -1.0376085182742925, -1.0068392370374892, -0.9187397379001893, -0.7887402860471101, -0.6392214353562293, -0.47654875992597784, -0.3089494978730164, -0.1364936265124562, 0.044633309210219775, 0.25387611839008817, 0.5094618689317836, 0.8163448818807704, 1.1470020165334407, 1.4568765647685389, 1.7082854142702992, 1.8971942256971341, 2.0320067505607957, 2.1285336680401525, 2.197539795730988, 2.2484422556558323, 2.2667610431503564, 2.2351963188552397, 2.1474123629689816, 2.012754167074242, 1.842555026982161, 1.6429349017803097, 1.4311126724442074, 1.2162227016527227, 1.0092007555839841, 0.8097517089931506, 0.6189759430513858, 0.4351483547379892, 0.274184689183651, 0.14407185974738576, 0.05750559966014323, 0.008717980548894605, -0.0052568446479373246, -0.04072634875261263, -0.08393141354573329, -0.11445036340074226, -0.14267012502927692, -0.18903203928096413, -0.2677218164319478, -0.4063996107542991, -0.6000983113948767, -0.8082739948339954, -0.9874316516562726, -1.1090295892383772, -1.1495957559765797, -1.116136683673526, -1.0246624367378843, -0.8870839774814798, -0.7324763214845121, -0.5685554738771879, -0.39977892579479146, -0.22622478083649425, -0.04435215205717115, 0.16726721504291303, 0.423393504543479, 0.728592056894507, 1.0655798087438442, 1.3912121151560148, 1.6602572727727611, 1.8622866104436875, 1.9968924479455998, 2.0804552223845327, 2.131035497976535, 2.1652580825750065, 2.1775985040182437, 2.1588451850334365, 2.0952212274654562, 1.9867066051694051, 1.8452762657361752, 1.6778681979400059, 1.4978971469962197, 1.3107388175815908, 1.1236678711888621, 0.9334838110662335, 0.7452411929410669, 0.5561179790792523, 0.38678539870086953, 0.24500513763853377, 0.1430025943386937, 0.0732323818024484, 0.03096457238464964, -0.03262566264398464, -0.0701624455806675, -0.09480563471522369, -0.12156557940945292, -0.16948770445028385, -0.2531758683980546, -0.40032946961185767, -0.6077402689292716, -0.8292752303810385, -1.0242337025815011, -1.1600510310038399, -1.2065584836853045, -1.1753188078275811, -1.0872711017820003, -0.9520990552617021, -0.8012354399247767, -0.6405461248552582, -0.46969690554732135, -0.29010737788892654, -0.10280199391416667, 0.10985848008780456, 0.3615574109713137, 0.6572684207014633, 0.9855846938083106, 1.305925780629741, 1.57301813702681, 1.7722920145225416, 1.8989423475613054, 1.9681427865574272, 2.002416562328761, 2.0173517473940823, 2.019186572724878, 2.005794791883889, 1.95934105099695, 1.8745145370892167, 1.7605817609985217, 1.6251219136426964, 1.479991454950227, 1.3268592117410236, 1.1667751000561895, 0.9964035110939486, 0.822440962811498, 0.6429068526649353, 0.4788100719186702, 0.33783715341070253, 0.2265840752465958, 0.1391976552251681, 0.06741025642003524, -0.014779871052271826, -0.03352004315639093, -0.04512759150045972, -0.0649627086536182, -0.1114208132495536, -0.19834851856790153, -0.3481838026360223, -0.5622307229200239, -0.7941411122034399, -1.0042907720675978, -1.1538420587792475, -1.2136950202388699, -1.1962487641880708, -1.1218094064184143, -0.9990414994519162, -0.8560106040170191, -0.7000978836800223, -0.5303663589777962, -0.3449438321271435, -0.1492381761394374, 0.06546767177016269, 0.3097990082019841, 0.5896115937737785, 0.8944823591117843, 1.1899560729402119, 1.4360138056813787, 1.61733243214922, 1.7328486937242278, 1.7922777766660642, 1.8145346280637573, 1.8103645354768156, 1.795724418749443, 1.7759272678954736, 1.737246560108905, 1.671393237805016, 1.5870794793022573, 1.4871303921556471, 1.3816007433959008, 1.268670267826523, 1.144324426926462, 1.0081394628447755, 0.8622354381415674, 0.7042249303689867, 0.5517615690054196, 0.41387825825510044, 0.2947082064521748, 0.19306922589730224, 0.09704298756333032, 0.009326238922482523, 0.01633122023840148, 0.022452711982121218, 0.013985356778982171, -0.026257981883522165, -0.11391620378886283, -0.2647629211345918, -0.4775470026625575, -0.7103705238398595, -0.9316624587336486, -1.09841351268702, -1.1830976311640635, -1.1908949343195454, -1.1359267631142271, -1.031772316665768, -0.8994824557545896, -0.7476660889829567, -0.5784624316107646, -0.38821417026153804, -0.1880671016052103, 0.02536395791434327, 0.25981870863190837, 0.5194626254821761, 0.7904490175019852, 1.0458618207292847, 1.257234955034333, 1.4121302692883706, 1.5146425308079823, 1.5670084537927749, 1.579469391974071, 1.5598313724424309, 1.52601207202497, 1.4904813014633953, 1.451026122868473, 1.4006972215390203, 1.343070895467245, 1.2749412421383486, 1.2067649544813552, 1.138132771128435, 1.0621819278492992, 0.974472034609328, 0.8690318947619773, 0.7399008491596883, 0.5999532322046814, 0.4635440929774046, 0.3386090278348607, 0.22584798257303304, 0.11518303064327141, 0.03466874672354205, 0.06479157511165691, 0.08809328553192823, 0.0887079400085232, 0.05575074373626855, -0.023830422240676878, -0.16509952421884616, -0.367778221883138, -0.595649675633098, -0.8225718903608649, -1.003404899082263, -1.1139583875279646, -1.1541446827613588, -1.126061193896663, -1.042221225368987, -0.9205073645831663, -0.7722481887904153, -0.602426979620012, -0.4093215825000243, -0.20786162670136754, 0.0009062247202891022, 0.22164218225539428, 0.4581947231950826, 0.6903370332461344, 0.8955546064661816, 1.0592956811059862, 1.1749664293235547, 1.255826242021953, 1.2997124901284247, 1.3064589137796123, 1.2789671072389668, 1.2286709555941433, 1.1760221775161115, 1.1315029896268636, 1.0933968952756297, 1.0565298166116912, 1.0196728411361236, 0.9891036200198037, 0.9648599729818541, 0.9407996863677266, 0.9060235092640728, 0.8470590895330712, 0.7513035148430205, 0.626429255740738, 0.4937366148766301, 0.3650310835110921, 0.24235073865920476, 0.12252467758054306, 0.060731838190324926, 0.11015601340365147, 0.1460435836304279, 0.15113821822128165, 0.12146612785613183, 0.05074014887990913, -0.07434474957022315, -0.26103170001712667, -0.47848553179917747, -0.7004768416764124, -0.8852149726690767, -1.0123103980070627, -1.0787697249461004, -1.0796020830895816, -1.0181688954518213, -0.9088209613441331, -0.7641764806494705, -0.5922499636987768, -0.3997986424736262, -0.2028763455725616, -0.005666394109529294, 0.19522872616557996, 0.4062162189612604, 0.6015820182119891, 0.7583697513892532, 0.8712582795258175, 0.9384617519148366, 0.9840278600864107, 1.0106474775234564, 1.01207094739378, 0.982625287639715, 0.926273658573383, 0.8667355256879532, 0.8208414602206312, 0.7934923043320088, 0.77284779793943, 0.760876110915817, 0.7613939448829168, 0.7773475020982372, 0.8012373951354596, 0.8154276008742516, 0.7978520433473851, 0.7342828151342787, 0.629641529783864, 0.5061761561177898, 0.37729689533808547, 0.24979306213047958, 0.12448041922551237, 0.08919492076870779, 0.15812167443243774, 0.19931041952965298, 0.2021925471409434, 0.1697931321486954, 0.10238068759319256, -0.008560472404744043, -0.1739838981839837, -0.37264531108865934, -0.5801685424873099, -0.7604556113587705, -0.8948204782464644, -0.9752257994520759, -0.9991361975183134, -0.9615787630659539, -0.867432337040363, -0.7296418529744993, -0.5626420048176387, -0.3803973223530593, -0.19511363310605684, -0.013418077643961213, 0.17033501313820867, 0.3584659734308967, 0.5224618465860608, 0.637590197224931, 0.7006578382779578, 0.717552452717027, 0.7213172842211657, 0.7223489128039671, 0.7126666558498024, 0.6818235955801392, 0.6325842958358655, 0.5825916915982472, 0.543250397040489, 0.5232879428825298, 0.5150442816313637, 0.5199717824676418, 0.5436819754468171, 0.5923263786858628, 0.6527568361339087, 0.7025555511439675, 0.7158915304632116, 0.6808119979307498, 0.6005325559102638, 0.4942040926568733, 0.37449099119194557, 0.2519463929764859, 0.1262333976669055, 0.11579262204764487, 0.19935297140426098, 0.23975219778803933, 0.23671274883985263, 0.19805424924221984, 0.12764113047209497, 0.021988372943668552, -0.12338807827042303, -0.29709132651594317, -0.47964620645463596, -0.6430598159021123, -0.7736582613207498, -0.8586986454837405, -0.895416145719004, -0.8755093015313637, -0.7968225865518093, -0.6728677442912845, -0.5248595190841384, -0.36607220277373564, -0.19882153955304352, -0.03420684340934903, 0.13311590258288078, 0.2966122708231765, 0.4322837192235238, 0.5143822438457029, 0.5368007149934341, 0.5124081026670249, 0.47913990026483033, 0.45557198470220717, 0.43430715237374795, 0.401903608165236, 0.3643636852075848, 0.33130040658643267, 0.30652805297935265, 0.2940008779197417, 0.2927587939939055, 0.30783050809774143, 0.34980815640871543, 0.420986970028171, 0.5044227944608286, 0.5759570734787435, 0.6111135020814685, 0.6022140621350875, 0.549899037160423, 0.4664140306383407, 0.362530264212113, 0.25189775155309607, 0.1293348157152387, 0.1266616228778356, 0.21429896909659288, 0.2521910049135126, 0.24605070109030536, 0.2049298118584874, 0.13480289926970615, 0.03503490437365441, -0.0946032074571008, -0.2437131681805774, -0.39427387419879667, -0.5316776123797997, -0.6489293808315713, -0.7277571898521367, -0.7635629710982694, -0.7537466999121932, -0.6958329154389133, -0.5964030481823691, -0.4790088427624645, -0.3520588752459828, -0.21105754743056082, -0.07127859625809559, 0.07336675067585414, 0.21048836793097633, 0.3200353908460596, 0.37905004541343357, 0.3802150255699084, 0.33621855298365716, 0.280275474171892, 0.23427156515826195, 0.19820465851131602, 0.1649727888692088, 0.1400191977191285, 0.12151027519937514, 0.11159172939121755, 0.10730225353221912, 0.11097873706408894, 0.13530625349620995, 0.1892778435816133, 0.2687299965651141, 0.36306393545154203, 0.44767090327547887, 0.4984092461523195, 0.5106880342891762, 0.4847057440404992, 0.4271428415210121, 0.3448738225454176, 0.24774075325752806, 0.12970601883930274, 0.11742156248713716, 0.19963186707131367, 0.23392897655887807, 0.2259090760543733, 0.18797197170888397, 0.12832125602911945, 0.0462604521895378, -0.06534342344727313, -0.19352381769709417, -0.31418077026655433, -0.4200202556591445, -0.5155360444113232, -0.5804687405479367, -0.6098982603203105, -0.6064090058058528, -0.5700504235133087, -0.501363297811854, -0.4204792402817672, -0.32669083758157536, -0.21553282263682852, -0.1052494556581483, 0.009676077685406409, 0.11598319730039179, 0.19550476462523206, 0.23747241677027014, 0.23586452016986711, 0.19407085095257945, 0.13369559159638347, 0.07567823409079621, 0.02896153575739153, -0.004298873447657819, -0.022396262728097253, -0.03605194934530043, -0.03926198750231576, -0.035032639209535824, -0.023236373494787778, 0.010323793084570713, 0.0698778933472429, 0.14905510878078596, 0.24336981828169735, 0.33143298014506384, 0.39116062958273234, 0.4195778000569038, 0.41548759717720657, 0.37967200794815875, 0.3170108593203505, 0.2309232353963414, 0.12015114875565308, 0.08985704255728875, 0.1540286396621408, 0.18320535326255544, 0.1822041476086873, 0.15901309361112898, 0.1163235724730849, 0.054367166720733995, -0.037412523021105475, -0.14235056814323105, -0.2369520688707469, -0.3112477837669191, -0.378464724140735, -0.4249286440778119, -0.4475146032117248, -0.4493834883874087, -0.42974730316272486, -0.3891812543613735, -0.34107643430826196, -0.276953393262031, -0.195418358714269, -0.11355472315946649, -0.030765085034234994, 0.043228183190332045, 0.09348249774229005, 0.12088012631171081, 0.12172162490703649, 0.09035926622544244, 0.03874202519409259, -0.019511231185598287, -0.07264401991890554, -0.10928714636991364, -0.12732969601976973, -0.14093765422909116, -0.14025990695609133, -0.12740695795920995, -0.10474633053087173, -0.06414528334109473, -0.005025672860895349, 0.06885678300018537, 0.1543087456575109, 0.23717443532594176, 0.29899698904827277, 0.33999987778870594, 0.3496432648125869, 0.3237058008592046, 0.2710587354067265, 0.19416517055816848, 0.09835476292790399, 0.05577483705764081, 0.09282651107817264, 0.11282382156523175, 0.12342687026766513, 0.12020471920602953, 0.0960824108482645, 0.0505401995170494, -0.020429304263786058, -0.0967790041378087, -0.1659279551387242, -0.21529543792121858, -0.256364160123597, -0.2844421667662726, -0.297856589183028, -0.29970271612496263, -0.2893539034181923, -0.2704082235396416, -0.24698492526764654, -0.2063808707340203, -0.14842644116296813, -0.08919532916705472, -0.03584412371424927, 0.005643721889469205, 0.0314029674491242, 0.04598487594287532, 0.04676999335681312, 0.02445687237030624, -0.014853147308390031, -0.06576785903048273, -0.11710524260725406, -0.15582320295849678, -0.176573252695862, -0.18935646644077736, -0.18363666000747048, -0.16405484737301573, -0.1336080310564772, -0.09259241039504079, -0.040577862467228214, 0.019325874212764115, 0.0874483215332447, 0.16006131759472053, 0.21804467415675924, 0.2625872135033003, 0.2746275952134384, 0.25052049001488425, 0.20527814656836432, 0.14249626139024107, 0.07007502445628173, 0.02620271426584808, 0.04248777222500173, 0.05503442832450269, 0.07070458318502881, 0.07796838152462775, 0.06744955737684395, 0.03801254476128396, -0.011155738745337996, -0.06246136934688987, -0.1072130711095656, -0.13672085128843992, -0.15799126043329648, -0.1709903412013928, -0.1760537249209349, -0.17590036746611917, -0.17142724726043085, -0.16655131895402003, -0.15689300523032637, -0.13171515495457303, -0.09105915952591408, -0.051167642828042696, -0.020604656780475357, -0.002988142998560587, 0.0062251061749086355, 0.009703817479887938, 0.009087026770645384, -0.005907562452238793, -0.033598361228969274, -0.07215306388423695, -0.11340941760595019, -0.1486640552111194, -0.16944328667841918, -0.1791998693376537, -0.16962601261600968, -0.14949446168950783, -0.1211074179376196, -0.0868204649831457, -0.04491820025663722, -0.003520471764878064, 0.040064704050758314, 0.09289585415829867, 0.14059043402333568, 0.1772390867847585, 0.1832218299812719, 0.16302684662842967, 0.12993365663912704, 0.08709697502595712, 0.04207368794599776, 0.009209135202207962, 0.014105429802971458, 0.0195933941999451, 0.031263443816651956, 0.03919912853944554, 0.03493799635029907, 0.019271290965777888, -0.006903483817580103, -0.03362377244826041, -0.054998252837319524, -0.06796003920612868, -0.07534123416449019, -0.07867871337814542, -0.08040018634257158, -0.08165370157946175, -0.08093420555388196, -0.0798346530866328, -0.07462916758421345, -0.06086072754907676, -0.0390044205458088, -0.01991706435281184, -0.006769959073132665, -0.001364380641177952, 0.00014765751994996377, -0.0015906443996861056, -0.0020717219232227672, -0.009762026027649112, -0.02586325676979638, -0.048606898431894606, -0.07238897578387682, -0.09323694920667454, -0.10556686839003496, -0.11067209692528007, -0.10301559506270065, -0.08904548962000869, -0.07092292766934072, -0.05134245873007965, -0.02700140532060884, -0.00538602653592651, 0.014015727533348885, 0.04027144255204177, 0.06763203023658886, 0.08802353065210868, 0.089497614702866, 0.0786461941246193, 0.06082172582854411, 0.03828111562175687, 0.017366054459406678, 5.660388760747083, 0.11090091779269576, 0.11085222139182901, 0.019363620118572348, 0.15233453592868115, 0.17280757751127096, 0.0674967031641901, 0.06268919704313253, 0.12957646431758185, 0.08443136898254801, 0.006523337682730155, 0.09044830316089439, 0.05951656430827086, 0.04564799035990572, 0.10459142436411192, 0.04660583215894767, 0.04116117276370781, 0.08802082402177579, -0.059406041996634525, -0.12470927866115537, 0.06370700519829979, 0.17410302304508377, 0.048395425327887195, -0.00176464771917044, 0.008053111066798206, -0.23591342753725913, 0.07817585974903712, 0.0618274702052786, 0.11141823929896544, 0.018587124704267884, -0.20191379554085073, 0.0203153537277368, 0.01152641476051053, 0.0955198858778476, -0.3470945594279216, 0.09984828552118817, 0.030661308685990624, -0.011069920936474237, 0.08707509173096523, -0.2823274404256719, 0.05568531255880554, 0.027698076886554557, 0.12320985475411698, -0.1864960693407447, 0.12257185744634448, 0.05906272995552356, 0.03952788772599092, 0.09917563163676571, -0.17591022536025405, 0.15857541918905096, 0.08337843071990275, 0.051691760813484165, 0.11064923700075616, -0.5274815715623389, 0.031499295220503785, 0.1739610192444668, 0.0712278163224279, 0.034530012203433234, 0.1414049302250429, -0.41383883802531946, 0.012282997122552049, 0.18746577791458827, 0.08975434511620653, 0.11944430425335313, 0.14024473670401966, -0.01273376575903357, -0.2199457783523709, 0.2310121304861817, -0.11668888341628, 0.0872395420495284, 0.06907543181649473, 0.1546689900833021, 0.13530012621132997, -0.28550615364670434, 0.2297137828528925, -0.0952541286074639, 0.07564810915043278, 0.04477540636844687, 0.21344069468218138, 0.24597543956634904, -0.15214606240073378, 0.0832086602547666, 0.07562814110737448, 0.045202275253559264, 0.2472304573600481, 0.27056053268903124, -0.9474922352558243, 0.1534692356694259, 0.0960841598027496, 0.08364005362276201, 0.2250917405363579, 0.30119255652059473, -0.16985728768023672, 0.1150544447670043, 0.10851459113632556, -0.010251727222650933, 0.18150796135313024, 0.3577366173926499, -0.09719826446651178, 0.1949552855764911, 0.08319860899659297, 0.18842033671802277, 0.4001256471082541, -0.3008843260504382, 0.21800423365782318, 0.009657141814684895, 0.04050376065648002, 0.012055034535596318, 0.04723781349023839, 0.027357797999027066, 0.04401936872492482, -0.011585543209288516, -0.020241266751320954, 0.013853913270400512, 0.03152171751131665, 0.03626264950206964, -0.004002924098509981, 0.0019524384141789662, 0.04557376611995977, 0.04689587233693882, -0.04535110995741706, 0.008392362282210821, 0.04602294219722357, 0.03476338874403365, 0.022972700145582725, -0.005153757586936929, 0.0355568780265424, 0.03931427708581918, 0.017420309854737893, 0.03568019577443648, 0.017147282949322808, 0.01351089844893255, -0.02229945798194918, 0.056312743482790965, 0.05272323090271892, 0.031929774447193075, 0.024214541914140963, 0.03430108398773276, 0.056817406716258775, 0.033559276901161866, 0.005536396610988331, -0.02212375881218565, 0.04999808466000309, 0.049912436425950946, 0.00014496172266909135, 0.0642646415296659, 0.04055247357022486, 0.05096242427049344, 0.058143652336753324, 0.01791724552194477, -0.031126416714188525, 0.05396975459437567, 0.06519065555476201, 0.020171821586354853, -0.007137145904665292, -0.044366821216570006, 0.044773323936341015, -0.13933658909482816, 0.040933873350602897, 0.056598128344910965, 0.001954644585288231, 0.000977470864534953, 0.04671131428099377, -0.11720660263178126, 0.044284732591251263, 0.057633756880261705, 0.005543212517712955, -0.08332078943379308, 0.055455710351477464, -0.02685693468576179, 0.03501468415044047, 0.03871341946594033, -0.12562307489789043, 0.0012014961056718112, 0.0014464564192219788, 0.0424619074075907, 0.008853285372093405, 0.0747204559302621, 0.03910218257295542, -0.07429681448992274, 0.025718703600075516, -0.007833840738856271, 0.01970556936948209, 0.020507259568529123, 0.03279874442432364, 0.01289548328874164, 0.002587145776194832, -0.06185505481801503, 0.016409595157757216, 0.02884747950231614, 0.051514147719970656, -0.010346712982038247, -0.011849637981575747, -0.017593144993444713, 0.04735431494017564, 0.03993448479265701, 0.05728068551389925, 0.04705504884871352, -0.024832428161245697, -0.03250709956221439, 0.07189574194220831, 0.06399908958404427, 0.06399801901833141, 0.08639852985303771, -0.007223282825438816, 0.06089895690575045, 0.07993295720357287, 0.03147640961042122, 0.06111028487701381, 0.2638154496267431, -0.975908644313543, 0.579419277709689, 0.7731327008366509, 0.32209968557606483, -0.8331550999369016, 0.475764969254031, 0.8545971163913072, 0.45850523916515035, -0.9042035814623289, 0.4168529536896095, 0.9797048801511677, 0.7562074849555284, -0.857146875848413, 0.39700444371084354, 0.888430184138322, 0.6807907538593452, -0.5885728388552957, 0.401886789084452, 0.8574443328594757, 0.908366357579776, -0.4550223284699498, 0.33635040270489897, 0.8801673309955819, -0.680418555734755, 0.5860850076717374, 0.948142221885497, -0.33207106364836414, 0.32650879587604453, 0.9297683791696421, -0.8185447672021202, 0.4319688288148593, -0.26844596755098143, 0.9490638637874805, 0.9688401003606735, -0.050381379433540305, 0.2491333680736925, 0.9392618159281817, -0.7405010437348808, 0.37313883493706795, -0.25289796896838007, 0.9538975129703756, 0.23928706649009238, 0.91031991518906, -0.9303342760150656, 0.21641671550801356, -0.20731575659808835, 0.9239193393526878, 0.9282227605940004, 0.36008151738721755, 0.1429356398824105, 0.9326156522932233, -0.9371719323802356, 0.16332483402675801, -0.2523221215468878, 0.936115001693066, 0.23468545789326742, 0.9126037379486794, -0.9886469301198263, 0.02524438650128064, -0.31993794637306056, 0.9260020260067955, 0.6841135304718361, 0.7335518220593772, 0.18630488848086063, 0.9556779618091167, -0.9258302701393858, -0.0737795460940994, -0.36618923593759417, 0.9166692978966207, 0.5342141529932641, 0.6801173691934994, 0.2395798565017325, 0.9437767317558083, -0.7823487595062403, -0.2853011252857347, -0.5897728594470466, 0.7487920891584678, -0.40646209599471467, 0.7260932351672129, 0.3304541887360455, 0.9494296045995145, 0.19537459413381214, 0.9290823151767833, -0.8993158950638035, -0.3721052528670991, -0.61768583167553, 0.7620255772612906, -0.5589900381749681, 0.8130878317563621, 0.1983726279002523, 0.9431401323486565, 0.21585020791400855, 0.9550605318819736, -0.7863239921337261, -0.5635867000100757, -0.6362075819516738, 0.7222783599608151, -0.7330436543941002, 0.654899081159086, -0.041537790148414924, 0.9895727859746714, -0.4960574286459455, -0.8561525303741229, 0.2456171904226765, 0.9393224186019183, -0.7027434950876533, -0.6505324698087284, -0.6447385245122795, 0.7072968178857084, -0.7731194040313766, 0.5670621307458416, -0.1393822162592691, 0.9787723198591284, -0.4211278855639116, -0.8779959381280319, 0.28121810758890253, 0.8713650428929307, -0.3175864347734062, -0.9225210708180674, -0.6343571536569108, 0.708835160701671, -0.8939625103179523, -0.4122866834644413, -0.9049713882401875, -0.3215889762049238, 0.3733842353971933, 0.8699067415256923, 0.22570093471161598, -0.9386693171188902, -0.6229530348972433, 0.7571564696370647, 0.07909925610071337, -0.9777422508800492, -0.8911662051920933, 0.4321655412292898, 0.8152357294441032, 1.3361805340357662, 0.7339024421892509, -0.6159809336709989, -0.5649026298763689, 0.7797834079719351, 0.7191749386637716, -0.6505178534954542, -0.15191859041710742, 0.9860917959408154, 0.7197457239707415, 0.9022986725845472, 0.8887492793060984, -0.24207287186337195, -0.5710606738300432, 0.8077987523427006, 0.9367575146417189, -0.300180717391921, 0.20210070891615112, 0.9553837671654224, 0.9726664875490384, -0.09005912592195833, -0.48058028304659317, 0.8265977118137382, 0.9602915588538169, -0.18693258061799667, 0.4405442976474694, 0.89366073705692, -0.04604327532642959, 0.9541491850962611, -0.08656360785087515, 0.9419085754315544, -0.04332848545131115, 0.9604813235743912, 0.052241806082489475, 0.9890435145382412, -0.03843659001490689, 0.9654818421543224, 0.07127704466540753, 1.2233309043710252, -0.05082988338591297, 0.8478005414978305, 0.048509357765261475, 0.9682350989433471, -0.034070870743097885, 0.9400396974748044, -0.06458791814487352, 0.9410066748860434, -0.0657794702826557, 0.955285560752248, -0.04527583903791798, 0.940146096480184, -0.042080464503948214, 0.9830474840783511, -0.04487374200610494, 0.948737948884767, 0.024799737622550937, 0.9647486183866736, 0.03396910674049522, 0.9600166440358856, 0.03916617573314774, 1.0194110078812944, -0.056205915475566436, 0.9587701752995872, -0.005580717971432734, 0.9472860876570643, -0.01420835622252391, 0.9638585305509639, 0.0284281900973552, 0.9532498772591851, -0.04977522781420884, 0.9400485636480893, 0.03344226896066661, 0.9432589645308982, -0.009067621925610203, 0.9420242230000914, -0.05426353049391402, 0.9444340188925574, 0.016031549941016573, 0.9420027495799677, 0.0049868648310224225, 0.9448581472746502, 0.020936647371878524, 0.9505970193957108, -0.05649745696076376, 0.9400731342648997, -0.03969532017353332, 0.9539693552663705, 0.02659096833587219, 0.9594290157238746, -0.0344978072748636, 0.9473008426803331, 0.03112074033610249, 0.9615589935515657, -0.02343201853644249, 0.9800693915147677, 0.02876050674996085, 0.9718229649056618, -0.05509361084674781, 0.9466990746928134, -0.04385567091512475, 0.945016814309487, -0.018468826386283468, 0.8966241692061178, 0.041093429957812164, 0.9442635006282752, 0.015398335892085046, 0.8852951273083088, -0.04077590136892974, 0.9441762945599054, -0.009540406213168469, 0.9457226512650272, -0.047240202892196055, 0.9599810592218689, 0.05874207742956021, 0.9831766188800471, 0.05171380623180539, 0.9558996309144544, -0.013651970571465265, 0.9838285772595973, -0.008415125312839063, 0.9518181057389645, -0.08741455171824833, 0.9471627206671843, 0.038205659257930714, 0.9606037293808917, 0.05971973547674303, 0.9498257577672513, -0.025582698762318147, 0.9451445345613436, -0.5947553791407774, 0.7615387663973163, 0.03150881115342256, 0.9510649343135964, -0.051582000909836265, 0.9449807671863416, 0.0346950106395415, 0.9542883465344996, 0.048256694472629, 0.9447555284229295, -0.02669739404743071, 0.9797039871994658, -0.23476760388762646, 0.9198168761908495, -0.04233458556923416, 1.0037630001386817, -0.07294075985932334, 0.9821701499190596, 0.045423417380385106, 0.9506107593227273, -0.016019290163819123, 0.9814213461147454, 0.3467407715321564, 1.511207348272224, 0.009240114458059934, 0.9655934916283394, 0.054051733854594906, 0.9450607801982238, 0.015607482227413242, 0.9700720887913988, 0.015206182717202615, 0.9585935392621973, 0.15163599336455338, 0.946691471256698, 0.029499710337544713, 1.0795493223007682, 0.16636529449801163, 0.9365166850290944, -0.009436038008588863, 0.951652093138416, 0.011277718104959634, 0.958492775569039, -0.12007175647984439, 0.9651434216154157, 0.05145263498638042, 1.0157572189071966, 0.18874610437033235, 0.9616937812429422, -0.011671643478761047, 0.9760629350536514, -0.009143468014596989, 0.9676629964568635, 0.04788476374489278, 0.9799080084471665, 0.1700903545447474, 0.9665344801166503, -0.017773366177639555, 0.944815036255423, -0.00961019223765672, 0.9614654224380108, -0.01791148395965837, 0.9655066889258898, -0.008109248742657145, -0.05222715191834749, 0.032403249138496584, 0.000448839844907692, 0.032645409702015994, -0.11053908161301133, -0.03262153171737247, -0.037052937843712906, 0.03483760878329025, 0.08797993002374795, 0.0005770714559388448, 0.04414294957585141, 0.014475525070373935, 0.008944396253946918, 0.009033029854454252, 0.021654590516214003, -0.029962995858560222, -0.051239097408931435, -0.0029268046412065287, 0.13957362820680796, -0.0339881544838362, -0.034323835120628615, 0.037978913770272266, 0.08761801425103502, 0.05638696034272269, 0.005626398160782996, 0.0045891779724163174, 0.06596623389304535]
Final objective value:     -17642.672904377763
)

Now let's evaluate our fits by plotting the residuals

julia

using CairoMakie
res = residuals(post, xopt)
fig = Figure(; size = (800, 600))
plotfields!(fig[1, 1], res[1], uvdist, x -> Comrade.measurement(x)[1, 1] / noise(x)[1, 1], axis_kwargs = (; ylabel = "RR Residual"))
plotfields!(fig[2, 1], res[1], uvdist, x -> Comrade.measurement(x)[2, 1] / noise(x)[2, 1], axis_kwargs = (; ylabel = "LR Residual"))
plotfields!(fig[1, 2], res[1], uvdist, x -> Comrade.measurement(x)[1, 2] / noise(x)[1, 2], axis_kwargs = (; ylabel = "RL Residual"))
plotfields!(fig[2, 2], res[1], uvdist, x -> Comrade.measurement(x)[2, 2] / noise(x)[2, 2], axis_kwargs = (; ylabel = "LL Residual"))
fig |> DisplayAs.PNG |> DisplayAs.Text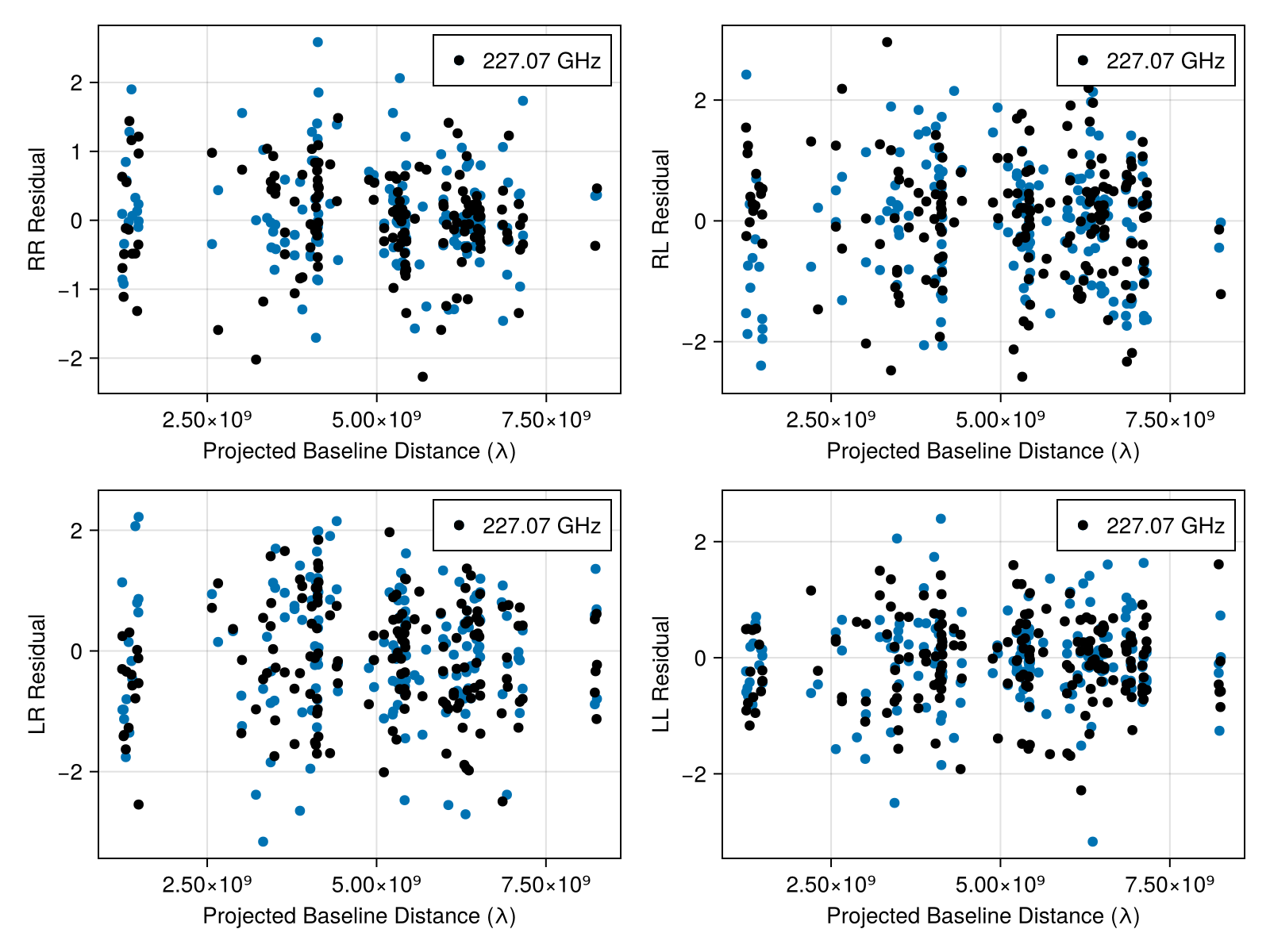

These look reasonable, although there may be some minor overfitting. Let's plot the results

julia

gpl = refinespatial(grid, 2)
img = intensitymap(skymodel(post, xopt), gpl)
fig = imageviz(
    img, adjust_length = true, colormap = :cmr_gothic, pcolormap = :rainbow1,
    pcolorrange = (0.0, 0.2), plot_total = false
);
fig |> DisplayAs.PNG |> DisplayAs.Text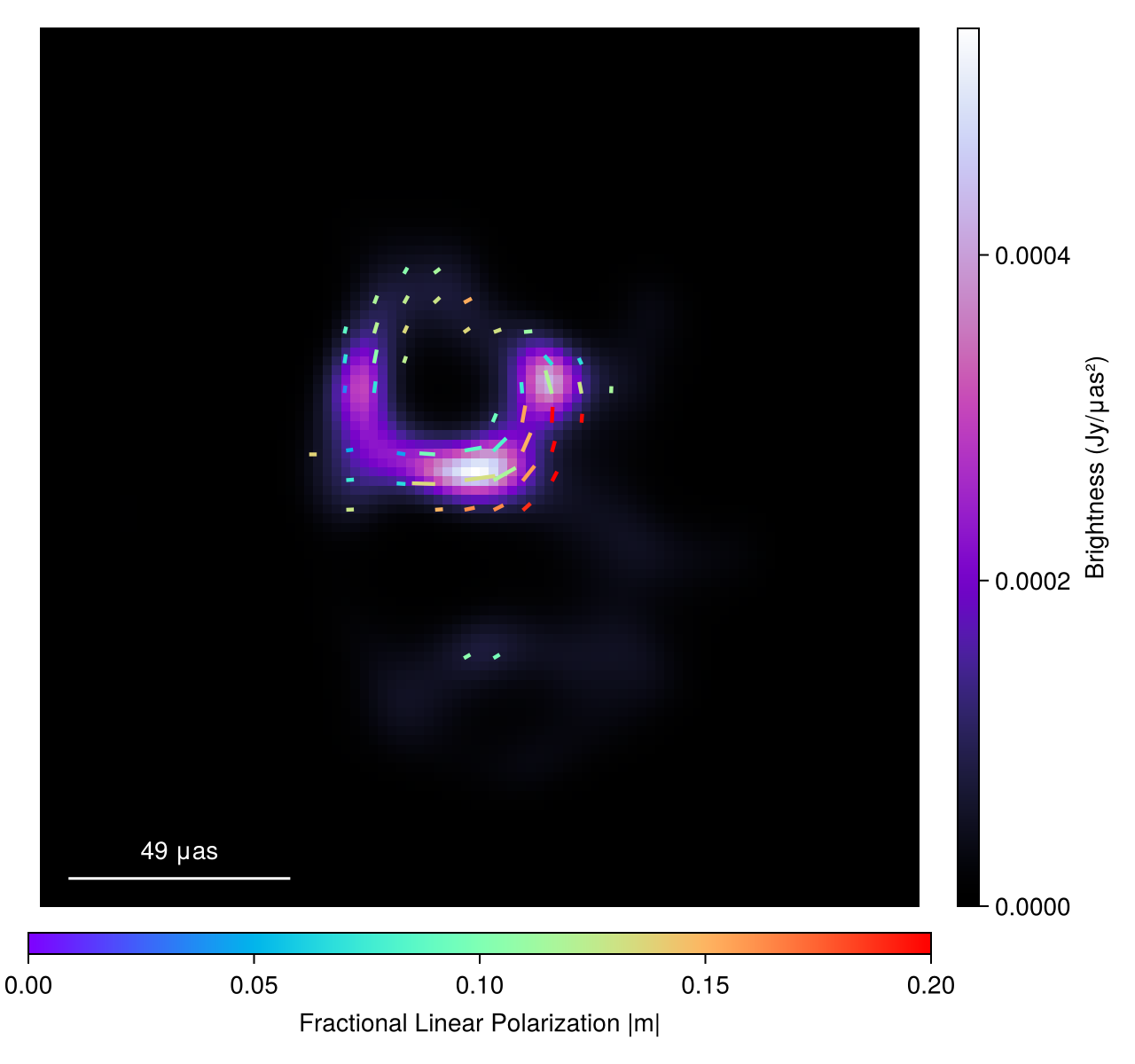

Note

The image looks a little noisy. This is an artifact of the MAP image. To get a publication quality image we recommend sampling from the posterior and averaging the samples. The results will be essentially identical to the results from EHTC VII.

We can also analyze the instrument model. For example, we can look at the gain ratios and products. To grab the ratios and products we can use the caltable function which will return analyze the gprat array and convert it to a uniform table. We can then plot the gain phases and amplitudes.

julia

gphase_ratio = caltable(xopt.instrument.gprat)
gamp_ratio = caltable(exp.(xopt.instrument.lgrat))

─────────┬───────────────────┬─────────────────────────────────────────────────────────────
      Ti │                Fr │    AA       AP       AZ       JC       LM       PV       SM
─────────┼───────────────────┼─────────────────────────────────────────────────────────────
 0.58 hr │ 227.070703125 GHz │  1.01  missing  missing  missing  missing    1.041  missing
 0.73 hr │ 227.070703125 GHz │ 1.012    1.048  missing  missing  missing    1.028  missing
 0.88 hr │ 227.070703125 GHz │ 1.045    0.988  missing  missing  missing     0.98  missing
  1.3 hr │ 227.070703125 GHz │ 1.014    1.032  missing  missing  missing    1.037  missing
 1.45 hr │ 227.070703125 GHz │ 0.996    1.002  missing  missing  missing    1.047  missing
 1.89 hr │ 227.070703125 GHz │ 1.048    0.956  missing  missing  missing    1.008  missing
 2.04 hr │ 227.070703125 GHz │ 1.047    1.035    1.023  missing  missing    0.995  missing
 2.46 hr │ 227.070703125 GHz │ 1.036     1.04    1.018  missing    1.036    1.017  missing
 2.61 hr │ 227.070703125 GHz │ 1.014    0.978    1.058  missing    1.054  missing  missing
 3.06 hr │ 227.070703125 GHz │ 1.032    1.025    1.035  missing    1.058    1.034  missing
 3.21 hr │ 227.070703125 GHz │ 1.006    0.978    1.051  missing    1.051  missing  missing
 3.62 hr │ 227.070703125 GHz │   1.0    1.066    1.041  missing    1.052     1.06  missing
 3.78 hr │ 227.070703125 GHz │ 1.018    0.969    1.055  missing    1.067     1.02  missing
 4.23 hr │ 227.070703125 GHz │ 0.993    0.957    1.046     0.87    1.042    1.058  missing
 4.37 hr │ 227.070703125 GHz │ 1.002    1.001    1.048    0.889    1.045    1.059  missing
 4.79 hr │ 227.070703125 GHz │ 1.006     0.92    1.057    0.974    1.036    1.039    0.882
 4.95 hr │ 227.070703125 GHz │ 1.001    1.001    1.043    1.009    1.078     1.04    0.928
 5.63 hr │ 227.070703125 GHz │ 1.026    0.992     1.02    1.021    1.033  missing    1.013
 6.15 hr │ 227.070703125 GHz │ 1.003     0.94    1.017    1.029    1.053  missing     0.99
 6.72 hr │ 227.070703125 GHz │ 0.988    0.983    1.048    1.041    1.059  missing    1.048
 7.23 hr │ 227.070703125 GHz │ 0.975    0.968    1.075    1.066    1.066  missing     1.09
 7.44 hr │ 227.070703125 GHz │ 0.993  missing    1.063    1.083    1.032  missing    1.063
─────────┴───────────────────┴─────────────────────────────────────────────────────────────

Plotting the phases first, we see large trends in the righ circular polarization phase. This is expected due to a lack of image centroid and the absense of absolute phase information in VLBI. However, the gain phase difference between the left and right circular polarization is stable and close to zero. This is expected since gain ratios are typically stable over the course of an observation and the constant offset was removed in the EHT calibration process.

julia

gphaseR = caltable(xopt.instrument.gpR)
fig = plotcaltable(gphaseR, gphase_ratio, labels = ["R Phase", "L/R Phase"]);
fig |> DisplayAs.PNG |> DisplayAs.Text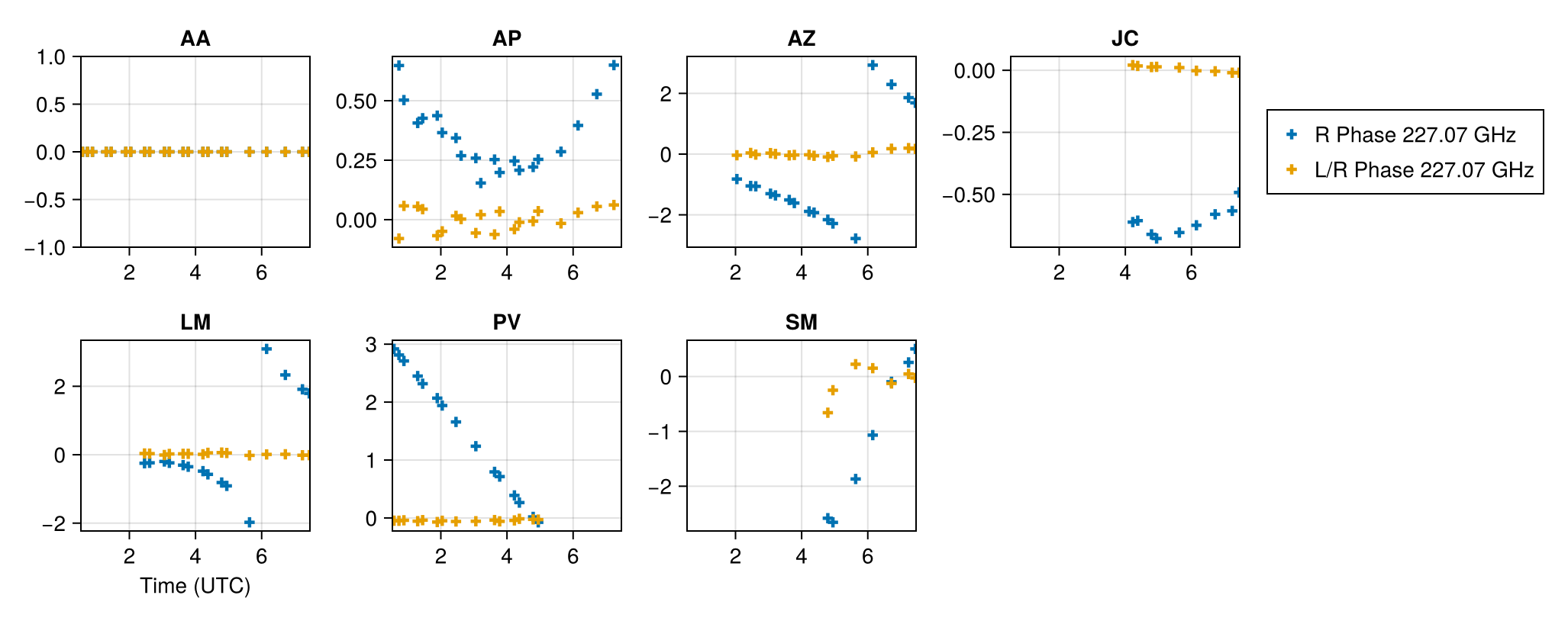

Moving to the amplitudes we see largely stable gain amplitudes on the right circular polarization except for LMT which is known and due to pointing issues during the 2017 observation. Again the gain ratios are stable and close to unity. Typically we expect that apriori calibration should make the gain ratios close to unity.

julia

gampr = caltable(exp.(xopt.instrument.lgR))
fig = plotcaltable(gampr, gamp_ratio, labels = ["R Amp", "L/R Amp"], axis_kwargs = (; limits = (nothing, (0.6, 1.3))));
fig |> DisplayAs.PNG |> DisplayAs.Text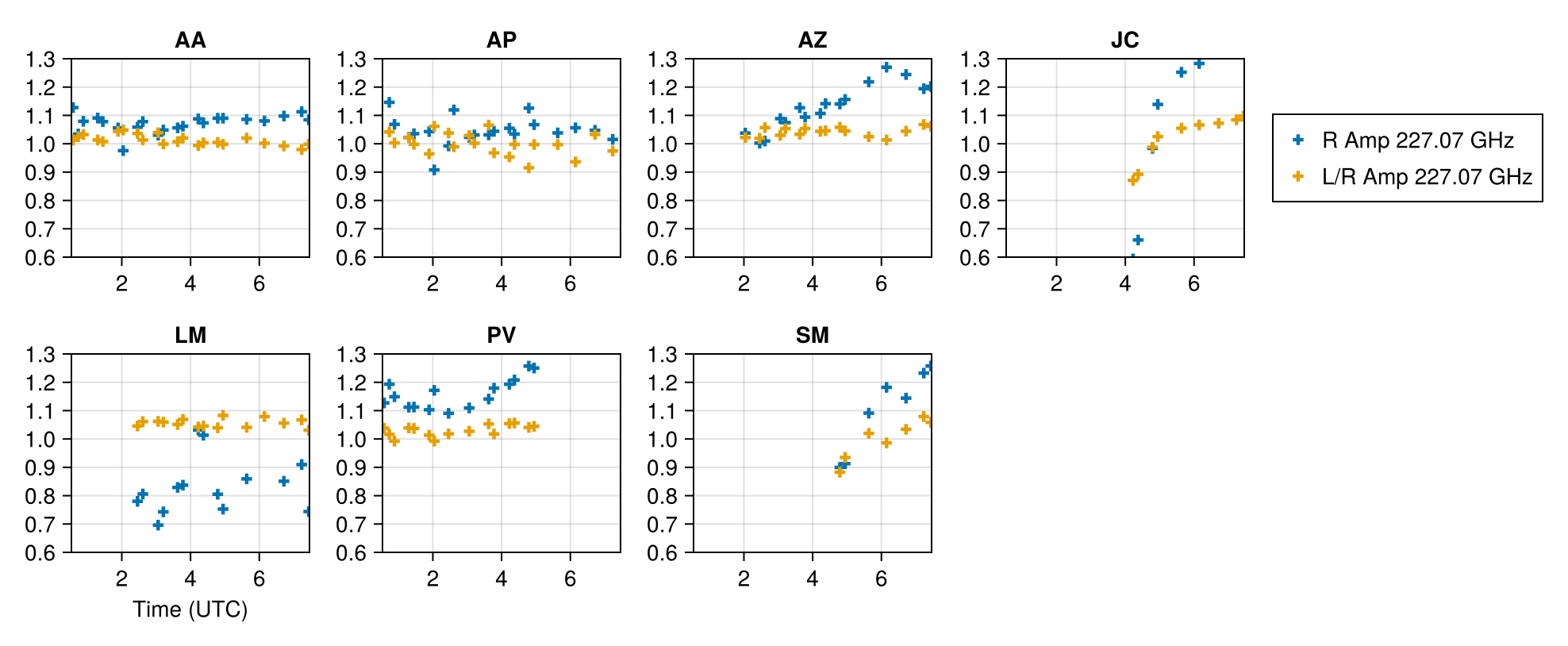

To sample from the posterior, you can then just use the sample function from AdvancedHMC like in the other imaging examples. For example

julia

using AdvancedHMC
chain = sample(rng, post, NUTS(0.8), 2_000, n_adapts = 1000, progress = true, initial_params = xopt)

This page was generated using Literate.jl.

Hamaker J.P, Bregman J.D., Sault R.J. (1996) [https://articles.adsabs.harvard.edu/pdf/1996A%26AS..117..137H] ↩︎
Pesce D. (2021) [https://ui.adsabs.harvard.edu/abs/2021AJ....161..178P/abstract] ↩︎

Polarized Image and Instrumental Modeling ​

Introduction to Polarized Imaging ​

Load the Data ​

Load the Data ​

Reconstructing the Image and Instrument Effects ​

Polarized Image and Instrumental Modeling

Introduction to Polarized Imaging

Load the Data

Load the Data

Reconstructing the Image and Instrument Effects